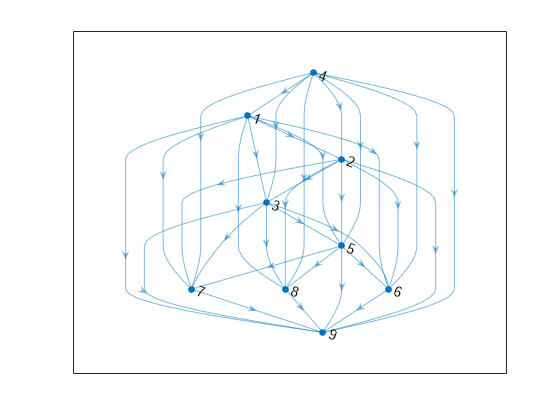
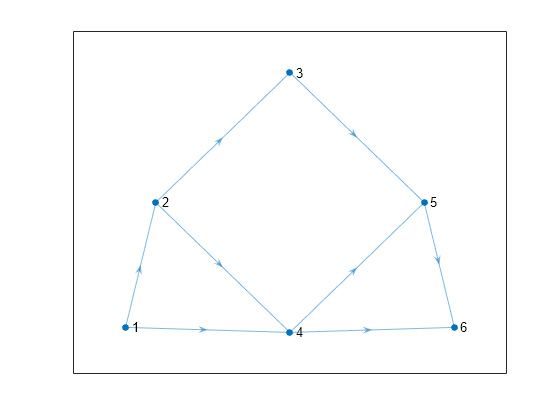
transclosure
Transitive closure
Syntax
Description
H = transclosure(G)G as a new graph, H. The nodes in
H are the same as those in G, but
H has additional edges. If there is a path from node
i to node j in G, then
there is an edge between node i and node j in
H. For multigraphs with multiple edges between the same two
nodes, the output graph replaces these with a single edge.
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced in R2015b
See Also
digraph | transreduction | conncomp | successors | predecessors