waterfall
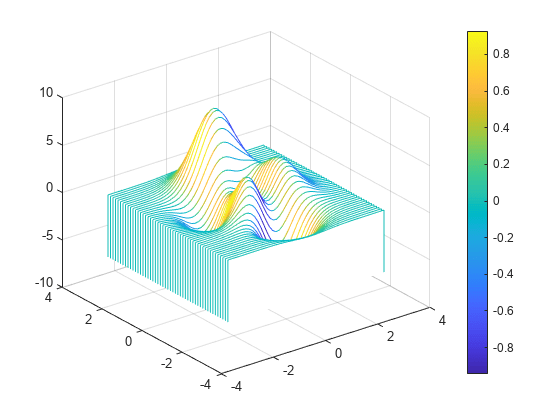
Waterfall plot
Syntax
Description
waterfall(
creates a waterfall plot, which is a mesh plot with a partial curtain along the
y dimension. This results in a "waterfall" effect. The
function plots the values in matrix X,Y,Z)Z as heights above a grid
in the xy-plane defined by
X and Y. The edge colors vary
according to the heights specified by Z.
waterfall( creates a waterfall
plot, and uses the column and row indices of the elements in
Z)Z as the x- and
y-coordinates.
waterfall(___,
sets properties of the waterfall plot using one or more name-value arguments.
For example, you can specify the color and thickness of the plot edges. For a
list of properties, see Patch Properties. (since R2024b)Name=Value)
waterfall( plots
into the axes specified by ax,___)ax instead of the current axes.
Specify the axes as the first input argument. This argument can be used with any
of the previous input syntaxes.
p = waterfall(___) returns the patch object.
Use p to modify the waterfall plot after it is created. For a
list of properties, see Patch Properties.
Examples
Input Arguments
Name-Value Arguments
Tips
To analyze the data as columns instead of rows, call
waterfallwith transposed arguments:[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); waterfall(X',Y',Z')
To create a mesh surface object instead of a patch object, use the
meshzfunction. To create a plot similar to a waterfall plot, set theMeshStyleproperty of the surface to'Row'.
Algorithms
The
XLim,YLim, andZLimproperties of the axes store the limits for the x-, y-, and z-axis. These limits are based on the ranges of theX,Y, andZinput arguments.The
CLimproperty of the axes determines the distribution of colors across the range ofC. For more information, see Control Colormap Limits.