Economic MPC Control of Ethylene Oxide Production
This example shows how to maximize the production of an ethylene oxide plant for profit using an economic MPC controller. This controller is implemented using a nonlinear MPC controller with a custom performance-based cost function.
Nonlinear Ethylene Oxidation Plant
Conversion of ethylene (C2H4) to ethylene oxide (C2H4O) occurs in a cooled, gas-phase catalytic reactor. Three reactions occur simultaneously in the well-mixed gas phase within the reactor:
C2H4 + 0.5*O2 -> C2H4O
C2H4 + 3*O2 -> 2*CO2 + 2*H2O
C2H4O + 2.5*O2 -> 2*CO2 + 2*H2O
The first reaction is wanted and the other two are unwanted because they reduce C2H4O production. A mixture of air and ethylene is continuously fed into the reactor. The first-principle nonlinear dynamic model of the reactor is implemented as a set of ordinary differential equations (ODEs) in the oxidationPlantCT function. For more information, see oxidationPlantCT.m.
The plant has four states:
Gas density in the reactor (
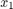 )
)C2H4 concentration in the reactor (
 )
)C2H4O concentration in the reactor (
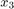 )
)Temperature in the reactor (
 )
)
The plant has three inputs:
C2H4 concentration in the feed (
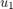 )
)Reactor cooling jacket temperature (
 )
)C2H4 feed rate (
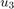 )
)
All variables in the model are scaled to be dimensionless and of unity order. The basic plant equations and parameters are obtained from [1] with some changes in input/output definitions and ordering.
The plant is asymptotically open-loop stable.
Control Objectives and Constraints
The primary control objective is to maximize the ethylene oxide (C2H4O) production rate (which in turn maximizes profit) at any steady-state operating point, given the availability of C2H4 in the feed stream.
The C2H4O production rate is defined as the product of the C2H4O concentration in the reactor (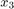 ) and the total volumetric flow rate exiting the reactor (
) and the total volumetric flow rate exiting the reactor (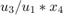 ).
).
The operating point is effectively determined by the three inputs. 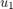 is the C2H4 concentration in the feed, which the MPC controller can manipulate.
is the C2H4 concentration in the feed, which the MPC controller can manipulate.  is the cooling jacket temperature, which keeps the temperature stable.
is the cooling jacket temperature, which keeps the temperature stable. 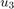 is the C2H4 feed rate, which indicates the available ethylene coming from an upstream process. A higher feed rate increases the achievable C2H4O production rate. In this example, both
is the C2H4 feed rate, which indicates the available ethylene coming from an upstream process. A higher feed rate increases the achievable C2H4O production rate. In this example, both  and
and 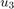 are measured disturbances.
are measured disturbances.
Optimal Production Rate at Initial Operating Point
At the initial condition, the cooling jacket temperature is 1.1 and the C2H4 availability is 0.175.
Tc = 1.1; C2H4Avalability = 0.175;
Compute the optimal C2H4O production rate by sweeping through the operating range of the C2H4 concentration in the feed (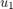 ) using
) using fsolve. Optimization Toolbox is required to run optimoptions and fsolve commands.
uRange = 0.1:0.1:3; EORate = zeros(length(uRange),1); optimopt = optimoptions('fsolve','Display','none'); for ct = 1:length(uRange) xRange = real(fsolve(@(x) oxidationPlantCT(x,[uRange(ct);Tc;C2H4Avalability]),rand(1,4),optimopt)); EORate(ct) = C2H4Avalability/uRange(ct)*xRange(3)*xRange(4); end figure plot(uRange,EORate) xlabel('C2H4 concentration in the feed') ylabel('C2H4O Production Rate')

The optimal C2H4O production rate of 0.0156 is achieved at 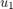 = 1.6. In other words, if the plant originally operates with a different C2H4 concentration in the feed, you expect the economic MPC controller to bring it to 1.6 such that the optimal C2H4O production rate is achieved.
= 1.6. In other words, if the plant originally operates with a different C2H4 concentration in the feed, you expect the economic MPC controller to bring it to 1.6 such that the optimal C2H4O production rate is achieved.
Nonlinear MPC Design
Economic MPC can be implemented with a nonlinear MPC controller. The prediction model has four states and three inputs (one MV and two MDs). In this example, since you do not need an output function, assume y = x.
nlobj = nlmpc(4,4,'MV',1,'MD',[2 3]); nlobj.States(1).Name = 'Den'; nlobj.States(2).Name = 'C2H4'; nlobj.States(3).Name = 'C2H4O'; nlobj.States(4).Name = 'Tc'; nlobj.MV.Name = 'CEin'; nlobj.MD(1).Name = 'Tc'; nlobj.MD(2).Name = 'Availability';
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
The nonlinear plant model is defined in oxidationPlantDT. It is a discrete-time model where a multistep explicit Euler method is used for integration. While this example uses a nonlinear plant model, you can also implement economic MPC using linear plant models.
nlobj.Model.StateFcn = 'oxidationPlantDT';
nlobj.Model.IsContinuousTime = false;
In general, to improve computational efficiency, it is best practice to provide an analytical Jacobian function for the prediction model. In this example, you do not provide one because the simulation is fast enough.
The relatively large sample time of 25 seconds used here is appropriate when the plant is stable and the primary objective is economic optimization. Prediction horizon is 2, which gives a prediction time of 50 seconds.
Ts = 25; nlobj.Ts = Ts; % Sample time nlobj.PredictionHorizon = 2; % Prediction horizon nlobj.ControlHorizon = 2; % Control horizon
All the states in the prediction model must be positive based on first principles. Therefore, specify a minimum bound of zero for all states.
nlobj.States(1).Min = 0; nlobj.States(2).Min = 0; nlobj.States(3).Min = 0; nlobj.States(4).Min = 0;
Plant input 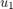 must stay within saturation limits between
must stay within saturation limits between 0.1 and 3.
nlobj.MV.Min = 0.1; nlobj.MV.Max = 3;
The rates of change of 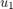 are also limited to +/-
are also limited to +/- 0.02/sec.
nlobj.MV.RateMin = -0.02*Ts; nlobj.MV.RateMax = 0.02*Ts;
Custom Cost Function for Economic MPC
Instead of using the standard quadratic objective function, a custom cost function is used as the replacement. You want to maximize the C2H4O production rate at the end of the prediction horizon.
f = -(u3/u1*x3*x4)
The negative sign in f is used to maximize production, since the controller minimizes f during optimization. For more information, see oxidationCostFcn.m.
nlobj.Optimization.CustomCostFcn = 'oxidationCostFcn';
nlobj.Optimization.ReplaceStandardCost = true;
Validate Custom Functions
Assume that the plant initially operates at u1 = 0.5.
u0 = 0.5;
Find the states at the steady state using fsolve.
x0 = real(fsolve(@(x) oxidationPlantCT(x,[u0;Tc;C2H4Avalability]),rand(1,4),optimopt));
The C2H4O production rate is 0.0138, far away from the optimal condition of 0.0156.
EORate0 = C2H4Avalability/u0*x0(3)*x0(4);
Validate the state function and cost function at the initial condition.
validateFcns(nlobj,x0,u0,[Tc C2H4Avalability]);
Model.StateFcn is OK. No output function specified. Assuming "y = x" in the prediction model. Optimization.CustomCostFcn is OK. Analysis of user-provided model, cost, and constraint functions complete.
You can compute the first move using the nlmpcmove function. It returns an MV of 1.0, indicating that economic MPC will increase the MV from 0.5 to 1, limited by the manipulated variable rate constraint.
mv = nlmpcmove(nlobj,x0,u0,zeros(1,4),[Tc C2H4Avalability]);
Simulink Model with Economic MPC Controller
Open the Simulink® model.
mdl = 'mpc_economicEO';
open_system(mdl)

The cooling jacket temperature is initially 1.1 and remains constant for the first 100 seconds. It then increases to 1.15, and therefore, reduces the optimal C2H4O production rate from 0.0156 to 0.0135.
The C2H4 availability is initially 0.175 and remains constant for the first 200 seconds. It then increases to 0.25, and therefore, increases the optimal C2H4O production rate from 0.0135 to 0.0195.
The model includes constant (zero) references for the four plant outputs. The Nonlinear MPC Controller block requires these reference signals, but they are ignored in the custom cost function.
The Plant subsystem calculates the plant states by integrating the ODEs in oxidationPlantCT.m. Assume all the states are measurable such that you do not need to implement a nonlinear state estimator in this example. The C2H4O plant output is the instantaneous C2H4O production rate, which is used for display purposes.
Simulate Model and Analyze Results
Run the simulation.
open_system([mdl '/MV']); open_system([mdl '/C2H4O']); sim(mdl)


Because the C2H4O plant operating at the initial condition is not optimal, its profit can be improved. In the first 100 seconds, the economic MPC controller gradually moves the plant to the true optimal condition under the same cooling jacket temperature and C2H4 availability constraints. It improves C2H4O production rate by:
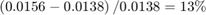
which could be worth millions of dollars per year in large-scale production.
In the next 100 seconds, the cooling jacket temperature increases from 1.1 to 1.15. The economic MPC controller moves the plant smoothly to the new optimal condition 0.0135 as expected.
In the next 100 seconds, the C2H4 availability increases from 0.175 to 0.25. The economic MPC controller is again able to move the plant the new optimal steady state 0.0195.
Close the Simulink model.
bdclose(mdl)
References
[1] H. Durand, M. Ellis, P. D. Christofides. "Economic model predictive control designs for input rate-of-change constraint handling and guaranteed economic performance." Computers and Chemical Engineering. Vol. 92,2016, pp 18-36.