Optimization and Control of Fed-Batch Reactor Using Nonlinear MPC
This example shows how to use nonlinear model predictive control to optimize batch reactor operation. The example also shows how to run a nonlinear MPC controller as an adaptive MPC controller and a time-varying MPC controller to quickly compare their performance.
Fed-Batch Chemical Reactor
The following irreversible and exothermic reactions occur in the batch reactor [1]:
A + B => C (desired product) C => D (undesired product)
The batch begins with the reactor partially filled with known concentrations of reactants A and B. The batch reacts for 0.5 hours, during which additional B can be added and the reactor temperature can be changed.
The nonlinear model of the batch reactor is defined in the fedbatch_StateFcn and fedbatch_OutputFcn functions. This system has the following inputs, states, and outputs.
Manipulated Variables
u1=u_B, flow rate ofBfeedu2=Tsp, reactor temperature setpoint, deg C
Measured disturbance
u3=c_Bin, concentration ofBin theBfeed flow
States
x1=V*c_A, mol ofAin the reactorx2=V*(c_A + c_C), mol ofA + Cin the reactorx3=V, liquid volume in the reactorx4=T, reactor temperature, K
Outputs
y1=V*c_C, amount of productCin the reactor, equivalent tox2-x1y2=q_r, heat removal rate, a nonlinear function of the statesy3=V, liquid volume in reactor
The goal is to maximize the production of C (y1) at the end of the batch process. During the batch process, the following operating constraints must be satisfied:
Hard upper bound on heat removal rate (
y2). Otherwise, temperature control fails.Hard upper bound on liquid volume in reactor (
y3) for safety.Hard upper and lower bounds on
Bfeed rate (u_B).Hard upper and lower bounds on reactor temperature setpoint (
Tsp).
Specify the nominal operating condition at the beginning of the batch process.
c_A0 = 10; c_B0 = 1.167; c_C0 = 0; V0 = 1; T0 = 50 + 273.15; c_Bin = 20;
Specify the nominal states.
x0 = zeros(3,1); x0(1) = c_A0*V0; x0(2) = x0(1) + c_C0*V0; x0(3) = V0; x0(4) = T0;
Specify the nominal inputs.
u0 = zeros(3,1); u0(2) = 40; u0(3) = c_Bin;
Specify the nominal outputs.
y0 = fedbatch_OutputFcn(x0,u0);
Nonlinear MPC Design to Optimize Batch Operation
Create a nonlinear MPC object with 4 states, 3 outputs, 2 manipulated variables, and 1 measured disturbance.
nlmpcobj_Plan = nlmpc(4, 3, 'MV', [1,2], 'MD', 3);
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
Given the expected batch duration Tf, choose the controller sample time Ts and prediction horizon.
Tf = 0.5; N = 50; Ts = Tf/N; nlmpcobj_Plan.Ts = Ts; nlmpcobj_Plan.PredictionHorizon = N;
If you set the control horizon equal to the prediction horizon, there will be 50 free control moves, which leads to a total of 100 decision variables because the plant has two manipulated variables. To reduce the number of decision variables, you can specify control horizon using blocking moves. Divide the prediction horizon into 8 blocks, which represents 8 free control moves. Each of the first seven blocks lasts seven prediction steps. Doing so reduces the number of decision variables to 16.
nlmpcobj_Plan.ControlHorizon = [7 7 7 7 7 7 7 1];
Specify the nonlinear model in the controller. The function fedbatch_StateFcnDT converts the continuous-time model to discrete time using a multi-step Forward Euler integration formula.
nlmpcobj_Plan.Model.StateFcn = @(x,u) fedbatch_StateFcnDT(x,u,Ts); nlmpcobj_Plan.Model.OutputFcn = @(x,u) fedbatch_OutputFcn(x,u); nlmpcobj_Plan.Model.IsContinuousTime = false;
Specify the bounds for feed rate of B.
nlmpcobj_Plan.MV(1).Min = 0; nlmpcobj_Plan.MV(1).Max = 1;
Specify the bounds for the reactor temperature setpoint.
nlmpcobj_Plan.MV(2).Min = 20; nlmpcobj_Plan.MV(2).Max = 50;
Specify the upper bound for the heat removal rate. The true constraint is 1.5e5. Since nonlinear MPC can only enforce constraints at the sampling instants, use a safety margin of 0.05e5 to prevent a constraint violation between sampling instants.
nlmpcobj_Plan.OV(2).Max = 1.45e5;
Specify the upper bound for the liquid volume in the reactor.
nlmpcobj_Plan.OV(3).Max = 1.1;
Since the goal is to maximize y1, the amount of C in the reactor at the end of the batch time, specify a custom cost function that replaces the default quadratic cost. Since y1 = x2-x1, define the custom cost to be minimized as x1-x2 using an anonymous function.
nlmpcobj_Plan.Optimization.CustomCostFcn = @(X,U,e,data) X(end,1)-X(end,2); nlmpcobj_Plan.Optimization.ReplaceStandardCost = true;
To configure the manipulated variables to vary linearly with time within each block, select piecewise linear interpolation. By default, nonlinear MPC keeps manipulated variables constant within each block, using piecewise constant interpolation, which might be too restrictive for an optimal trajectory planning problem.
nlmpcobj_Plan.Optimization.MVInterpolationOrder = 1;
Use the default nonlinear programming solver fmincon to solve the nonlinear MPC problem. For this example, set the solver step tolerance to help achieve first order optimality.
nlmpcobj_Plan.Optimization.SolverOptions.StepTolerance = 1e-8;
Before carrying out optimization, check whether all the custom functions satisfy NLMPC requirements using the validateFcns command.
validateFcns(nlmpcobj_Plan, x0, u0(1:2), u0(3));
Model.StateFcn is OK. Model.OutputFcn is OK. Optimization.CustomCostFcn is OK. Analysis of user-provided model, cost, and constraint functions complete.
Analysis of Optimization Results
Find the optimal trajectories for the manipulated variables such that production of C is maximized at the end of the batch process. To do so, use the nlmpcmove function.
fprintf('\nOptimization started...\n'); [~,~,Info] = nlmpcmove(nlmpcobj_Plan,x0,u0(1:2),zeros(1,3),u0(3)); fprintf(' Expected production of C (y1) is %g moles.\n',Info.Yopt(end,1)); fprintf(' First order optimality is satisfied (Info.ExitFlag = %i).\n',... Info.ExitFlag); fprintf('Optimization finished...\n');
Optimization started... Slack variable unused or zero-weighted in your custom cost function. All constraints will be hard. Expected production of C (y1) is 2.02353 moles. First order optimality is satisfied (Info.ExitFlag = 1). Optimization finished...
The discretized model uses a simple Euler integration, which could be inaccurate. To check this, integrate the model using the ode15s command for the calculated optimal MV trajectory.
Nstep = size(Info.Xopt,1) - 1; t = 0; X = x0'; t0 = 0; for i = 1:Nstep u_in = [Info.MVopt(i,1:2)'; c_Bin]; ODEFUN = @(t,x) fedbatch_StateFcn(x, u_in); TSPAN = [t0, t0+Ts]; Y0 = X(end,:)'; [TOUT,YOUT] = ode15s(ODEFUN,TSPAN,Y0); t = [t; TOUT(2:end)]; X = [X; YOUT(2:end,:)]; t0 = t0 + Ts; end nx = size(X,1); Y = zeros(nx,3); for i = 1:nx Y(i,:) = fedbatch_OutputFcn(X(i,:)',u_in)'; end fprintf('\n Actual Production of C (y1) is %g moles.\n',X(end,2)-X(end,1)); fprintf(' Heat removal rate (y2) satisfies the upper bound.\n');
Actual Production of C (y1) is 2.0228 moles. Heat removal rate (y2) satisfies the upper bound.
In the top plot of the following figure, the actual production of C agrees with the expected production of C calculated from nlmpcmove. In the bottom plot, the heat removal rate never exceeds its hard constraint.
figure subplot(2,1,1) plot(t,Y(:,1),(0:Nstep)*Ts, Info.Yopt(:,1),'*') axis([0 0.5 0 Y(end,1) + 0.1]) legend({'Actual','Expected'},'location','northwest') title('Mol C in reactor (y1)') subplot(2,1,2) tTs = (0:Nstep)*Ts; t(end) = 0.5; plot(t,Y(:,2),'-',[0 tTs(end)],1.5e5*ones(1,2),'r--') axis([0 0.5 0.8e5, 1.6e5]) legend({'q_r','Upper Bound'},'location','southwest') title('Heat removal rate (y2)')

Close examination of the heat removal rate shows that it can exhibit peaks and valleys between the sampling instants as reactant compositions change. Consequently, the heat removal rate exceeds the specified maximum of 1.45e5 (around t = 0.35 h) but stays below the true maximum of 1.5e5.
The following figure shows the optimal trajectory of planned adjustments in the B feed rate (u1), and the reactor temperature (x4) and its setpoint (u2).
figure subplot(2,1,1) stairs(tTs,Info.MVopt(:,1)) title('Feed rate of B (u1)') subplot(2,1,2) plot(tTs,Info.MVopt(:,2),'*',t,X(:,4)-273.15,'-',... [0 0.5],[20 20],'r--',[0 0.5],[50 50],'r--') axis([0 0.5 15 55]) title('Reactor temperature and its setpoint') legend({'Setpoint','Actual'},'location','southeast')
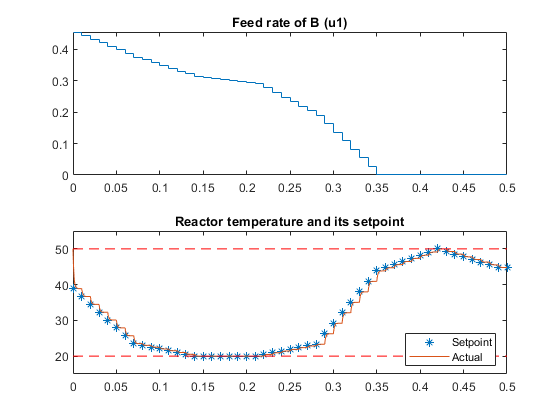
The trajectory begins with a relatively high feed rate, which increases c_B and the resulting C production rate. To prevent exceeding the heat removal rate constraint, reactor temperature and feed rate must decrease. The temperature eventually hits its lower bound and stays there until the reactor is nearly full and the B feed rate must go to zero. The temperature then increases to its maximum (to increase C production) and finally drops slightly (to reduce D production, which is favored at higher temperatures).
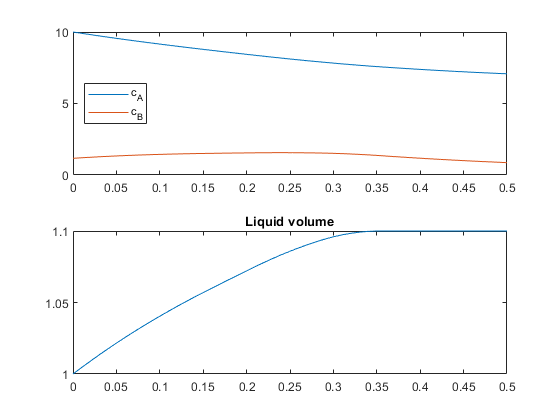
The top plot of the following figure shows the consumption of c_A, which tends to reduce C production. To compensate, the plan first increases c_B, and when that is no longer possible (the reactor liquid volume must not exceed 1.1), the plan makes optimal use of the temperature. In the bottom plot of the following figure, the liquid volume never exceeds its upper bound.
figure
subplot(2,1,1)
c_A = X(:,1)./X(:,3);
c_B = (c_Bin*X(:,3) + X(:,1) + V0*(c_B0 - c_A0 - c_Bin))./X(:,3);
plot(t,[c_A, c_B])
legend({'c_A','c_B'}, 'location', 'west')
subplot(2,1,2)
plot(tTs,Info.Yopt(:,3))
title('Liquid volume')
Nonlinear MPC Design for Tracking the Optimal C Product Trajectory
To track the optimal trajectory of product C calculated above, you design another nonlinear MPC controller with the same prediction model and constraints. However, use the standard quadratic cost and default horizons for tracking purposes.
To simplify the control task, assume that the optimal trajectory of the B feed rate is implemented in the plant and the tracking controller considers it to be a measured disturbance. Therefore, the controller uses the reactor temperature setpoint as its only manipulated variable to track the desired y1 profile.
Create the tracking controller.
nlmpcobj_Tracking = nlmpc(4,3,'MV',2,'MD',[1,3]); nlmpcobj_Tracking.Ts = Ts; nlmpcobj_Tracking.Model = nlmpcobj_Plan.Model; nlmpcobj_Tracking.MV = nlmpcobj_Plan.MV(2); nlmpcobj_Tracking.OV = nlmpcobj_Plan.OV; nlmpcobj_Tracking.Weights.OutputVariables = [1 0 0]; % track y1 only nlmpcobj_Tracking.Weights.ManipulatedVariablesRate = 1e-6; % aggressive MV
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
Obtain the C production (y1) reference signal from the optimal plan trajectory.
Cref = Info.Yopt(:,1);
Obtain the feed rate of B (u1) from the optimal plan trajectory. The feed concentration of B (u3) is a constant.
MD = [Info.MVopt(:,1) c_Bin*ones(N+1,1)];
First, run the tracking controller in nonlinear MPC mode.
[X1,Y1,MV1,et1] = fedbatch_Track(nlmpcobj_Tracking,x0,u0(2),N,Cref,MD);
fprintf('\nNonlinear MPC: Elapsed time = %g sec. Production of C = %g mol\n',et1,Y1(end,1));
Nonlinear MPC: Elapsed time = 1.64033 sec. Production of C = 2.01131 mol
Second, run the controller as an adaptive MPC controller.
nlmpcobj_Tracking.Optimization.RunAsLinearMPC = 'Adaptive'; [X2,Y2,MV2,et2] = fedbatch_Track(nlmpcobj_Tracking,x0,u0(2),N,Cref,MD); fprintf('\nAdaptive MPC: Elapsed time = %g sec. Production of C = %g mol\n',et2,Y2(end,1));
Adaptive MPC: Elapsed time = 1.1804 sec. Production of C = 2.01567 mol
Third, run the controller as a time-varying MPC controller.
nlmpcobj_Tracking.Optimization.RunAsLinearMPC = 'TimeVarying'; [X3,Y3,MV3,et3] = fedbatch_Track(nlmpcobj_Tracking,x0,u0(2),N,Cref,MD); fprintf('\nTime-varying MPC: Elapsed time = %g sec. Production of C = %g mol\n',et3,Y3(end,1));
Time-varying MPC: Elapsed time = 0.854202 sec. Production of C = 2.02346 mol
In the majority of MPC applications, linear MPC solutions, such as Adaptive MPC and Time-varying MPC, provide performance that is comparable to the nonlinear MPC solution, while consuming less resources and executing faster. In these cases, nonlinear MPC often represents the best control results that MPC can achieve. By running a nonlinear MPC controller as a linear MPC controller, you can assess whether implementing a linear MPC solution is good enough in practice.
In this example, all three methods come close to the optimal C production obtained in the planning stage.
figure plot(Ts*(0:N),[Y1(:,1) Y2(:,1) Y3(:,1)]) title('Production of C') legend({'NLMPC','Adaptive','TimeVarying'},'location','northwest')

The unexpected result is that time-varying MPC produces more C than nonlinear MPC. The explanation is that the model linearization approaches used in the adaptive and time-varying modes result in a violation of the heat removal constraint, which results in a higher C production.
figure plot(Ts*(0:N),[Y1(:,2) Y2(:,2) Y3(:,2) 1.5e5*ones(N+1,1)]) title('Heat removal rate') legend({'NLMPC','Adaptive','TimeVarying','Constraint'},'location','southwest')
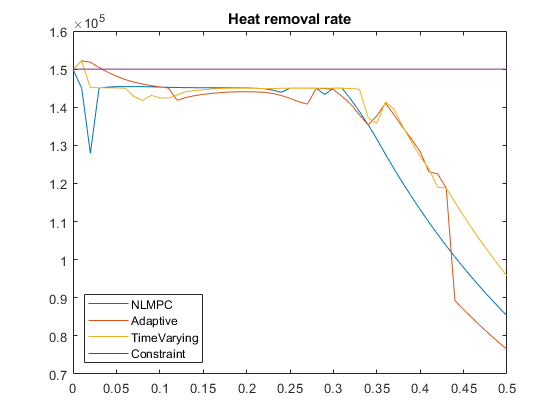
The adaptive MPC mode uses the plant states and inputs at the beginning of each control interval to obtain a single linear prediction model. This approach does not account for the known future changes in the feed rate, for example.
The time-varying method avoids this issue. However, at the start of the batch it assumes (by default) that the states will remain constant over the horizon. It corrects for this once it obtains its first solution (using data in the opts variable), but its initial choice of reactor temperature is too high, resulting in an early q_r constraint violation.
References
[1] Srinivasan, B., S. Palanki, and D. Bonvin, "Dynamic optimization of batch processes I. Characterization of the nominal solution", Computers and Chemical Engineering, vol. 27 (2003), pp. 1-26.