solve
Solve structural analysis, heat transfer, or electromagnetic analysis problem
Syntax
Description
results = solve(fem,FrequencyRange=[omega1,omega2])fem for all modes in the frequency range
[omega1,omega2]. Define omega1 as
slightly lower than the lowest expected frequency and omega2
as slightly higher than the highest expected frequency. For example, if the
lowest expected frequency is zero, then use a small negative value for
omega1.
results = solve(fem,DecayRange=[lambda1,lambda2])fem for all modes in the
decay range [lambda1,lambda2]. The resulting modes enable
you to:
Use the modal superposition method to speed up a transient thermal analysis.
Extract the reduced modal system to use, for example, in Simulink®.
results = solve(fem,Snapshots=Tmatrix)fem using proper
orthogonal decomposition (POD). You can use the resulting modes to speed up a
transient thermal analysis or, if your thermal model is linear, to extract the
reduced modal system.
results = solve(fem,tlist,ModalResults=thermalModalR)results = solve(fem,tlist,ModalResults=structuralModalR)results = solve(fem,flist,ModalResults=structuralModalR)
Examples
Solve a static structural problem representing a bimetallic cable under tension.
Create and plot a bimetallic cable geometry.
gm = multicylinder([0.01 0.015],0.05); pdegplot(gm,FaceLabels="on", ... CellLabels="on", ... FaceAlpha=0.5)

Create an femodel object for static structural analysis and include the geometry.
model = femodel(AnalysisType="structuralStatic", ... Geometry=gm);
Specify Young's modulus and Poisson's ratio for each metal.
model.MaterialProperties(1) = ... materialProperties(YoungsModulus=110E9, ... PoissonsRatio=0.28); model.MaterialProperties(2) = ... materialProperties(YoungsModulus=210E9, ... PoissonsRatio=0.3);
Specify that faces 1 and 4 are fixed boundaries.
model.FaceBC([1,4]) = faceBC(Constraint="fixed");Specify the surface traction for faces 2 and 5.
model.FaceLoad([2,5]) = faceLoad(SurfaceTraction=[0;0;100]);
Generate a mesh and solve the problem.
model = generateMesh(model); R = solve(model)
R =
StaticStructuralResults with properties:
Displacement: [1×1 FEStruct]
Strain: [1×1 FEStruct]
Stress: [1×1 FEStruct]
VonMisesStress: [23098×1 double]
Mesh: [1×1 FEMesh]
The solver finds the values of the displacement, stress, strain, and von Mises stress at the nodal locations. To access these values, use R.Displacement, R.Stress, and so on. The displacement, stress, and strain values at the nodal locations are returned as FEStruct objects with the properties representing their components. Note that properties of an FEStruct object are read-only.
R.Displacement
ans =
FEStruct with properties:
ux: [23098×1 double]
uy: [23098×1 double]
uz: [23098×1 double]
Magnitude: [23098×1 double]
R.Stress
ans =
FEStruct with properties:
sxx: [23098×1 double]
syy: [23098×1 double]
szz: [23098×1 double]
syz: [23098×1 double]
sxz: [23098×1 double]
sxy: [23098×1 double]
R.Strain
ans =
FEStruct with properties:
exx: [23098×1 double]
eyy: [23098×1 double]
ezz: [23098×1 double]
eyz: [23098×1 double]
exz: [23098×1 double]
exy: [23098×1 double]
Plot the deformed shape with the z-component of normal stress.
pdeplot3D(R.Mesh, ... ColorMapData=R.Stress.szz, ... Deformation=R.Displacement)

Solve for the transient response of a thin 3-D plate under a harmonic load at the center.
Create a geometry of a thin 3-D plate and plot it.
gm = multicuboid([5,0.05],[5,0.05],0.01);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5)
Zoom in to see the face labels on the small plate at the center.
figure
pdegplot(gm,FaceLabels="on",FaceAlpha=0.25)
axis([-0.2 0.2 -0.2 0.2 -0.1 0.1])
Create an femodel object for transient structural analysis and include the geometry.
model = femodel(AnalysisType="structuralTransient", ... Geometry=gm);
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
model.MaterialProperties = ... materialProperties(YoungsModulus=210E9, ... PoissonsRatio=0.3, ... MassDensity=7800);
Specify that all faces on the periphery of the thin 3-D plate are fixed boundaries.
model.FaceBC(5:8) = faceBC(Constraint="fixed");Apply a sinusoidal pressure load on the small face at the center of the plate.
First, define a sinusoidal load function, sinusoidalLoad, to model a harmonic load. This function accepts the load magnitude (amplitude), the location and state structure arrays, frequency, and phase. Because the function depends on time, it must return a matrix of NaN of the correct size when state.time is NaN. Solvers check whether a problem is nonlinear or time-dependent by passing NaN state values and looking for returned NaN values.
function Tn = sinusoidalLoad(load,location,state,Frequency,Phase) if isnan(state.time) Tn = NaN*(location.nx); return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Transient model excited with harmonic load Tn = load.*sin(Frequency.*state.time + Phase); end
Now, apply a sinusoidal pressure load on face 12 by using the sinusoidalLoad function.
Pressure = 5e7;
Frequency = 25;
Phase = 0;
pressurePulse = @(location,state) ...
sinusoidalLoad(Pressure,location,state,Frequency,Phase);
model.FaceLoad(12) = faceLoad(Pressure=pressurePulse);Generate a mesh with linear elements.
model = generateMesh(model,GeometricOrder="linear",Hmax=0.2);Specify zero initial displacement and velocity.
model.CellIC = cellIC(Displacement=[0;0;0],Velocity=[0;0;0]);
Solve the model.
tlist = linspace(0,1,300); R = solve(model,tlist);
The solver finds the values of the displacement, velocity, and acceleration at the nodal locations. To access these values, use R.Displacement, R.Velocity, and so on. The displacement, velocity, and acceleration values are returned as FEStruct objects with the properties representing their components. Note that properties of an FEStruct object are read-only.
R.Displacement
ans =
FEStruct with properties:
ux: [2217×300 double]
uy: [2217×300 double]
uz: [2217×300 double]
Magnitude: [2217×300 double]
R.Velocity
ans =
FEStruct with properties:
vx: [2217×300 double]
vy: [2217×300 double]
vz: [2217×300 double]
Magnitude: [2217×300 double]
R.Acceleration
ans =
FEStruct with properties:
ax: [2217×300 double]
ay: [2217×300 double]
az: [2217×300 double]
Magnitude: [2217×300 double]
Perform frequency response analysis of a tuning fork.
Create an femodel object for frequency response analysis and include the geometry of a tuning fork in the model.
model = femodel(AnalysisType="structuralFrequency", ... Geometry="TuningFork.stl");
Specify Young's modulus, Poisson's ratio, and the mass density to model linear elastic material behavior. Specify all physical properties in consistent units.
model.MaterialProperties = ... materialProperties(YoungsModulus=210E9, ... PoissonsRatio=0.3, ... MassDensity=8000);
Identify faces for applying boundary constraints and loads by plotting the geometry with the face labels.
figure("units","normalized","outerposition",[0 0 1 1]) pdegplot(model,FaceLabels="on") view(-50,15) title("Geometry with Face Labels")

Impose sufficient boundary constraints to prevent rigid body motion under applied loading. Typically, you hold a tuning fork by hand or mount it on a table. To create a simple approximation of this boundary condition, fix a region near the intersection of tines and the handle (faces 21 and 22).
model.FaceBC([21,22]) = faceBC(Constraint="fixed");Specify the pressure loading on a tine (face 11) as a short rectangular pressure pulse.
model.FaceLoad(11) = faceLoad(Pressure=1);
Generate a mesh. Specify the Hface name-value argument to generate a finer mesh for small faces.
model = generateMesh(model,Hmax=0.005,Hface={[3 4 9 10],0.0003});In the frequency domain, this pressure pulse is a unit load uniformly distributed across all frequencies.
flist = linspace(0,4000,150); R = solve(model,2*pi*flist);
Plot the vibration frequency of the tine tip, which is face 12. Find nodes on the tip face and plot the y-component of the displacement over the frequency, using one of these nodes.
excitedTineTipNodes = findNodes(model.Mesh,"region",Face=12); tipDisp = R.Displacement.uy(excitedTineTipNodes(1),:); figure plot(flist,abs(tipDisp)) xlabel("Frequency"); ylabel("|Y-Displacement|");

Find the fundamental (lowest) mode of a 2-D cantilevered beam, assuming prevalence of the plane-stress condition.
Specify geometric and structural properties of the beam, along with a unit plane-stress thickness.
length = 5; height = 0.1; E = 3E7; nu = 0.3; rho = 0.3/386;
Create a geometry.
gdm = [3;4;0;length;length;0;0;0;height;height]; g = decsg(gdm,'S1',('S1')');
Create an femodel object for modal structural analysis and include the geometry.
model = femodel(Analysistype="structuralModal", ... Geometry=g);
Define a maximum element size (five elements through the beam thickness).
hmax = height/5;
Generate a mesh.
model=generateMesh(model,Hmax=hmax);
Specify the structural properties and boundary constraints.
model.MaterialProperties = ... materialProperties(YoungsModulus=E, ... MassDensity=rho, ... PoissonsRatio=nu); model.EdgeBC(4) = edgeBC(Constraint="fixed");
Compute the analytical fundamental frequency (Hz) using the beam theory.
I = height^3/12; analyticalOmega1 = 3.516*sqrt(E*I/(length^4*(rho*height)))/(2*pi)
analyticalOmega1 = 126.9498
Specify a frequency range that includes an analytically computed frequency and solve the model.
R = solve(model,FrequencyRange=[0,1e6])
R =
ModalStructuralResults with properties:
NaturalFrequencies: [32×1 double]
ModeShapes: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
The solver finds natural frequencies and modal displacement values at nodal locations. To access these values, use R.NaturalFrequencies and R.ModeShapes.
R.NaturalFrequencies/(2*pi)
ans = 32×1
105 ×
0.0013
0.0079
0.0222
0.0433
0.0711
0.0983
0.1055
0.1462
0.1930
0.2455
0.2948
0.3034
0.3664
0.4342
0.4913
⋮
R.ModeShapes
ans =
FEStruct with properties:
ux: [6511×32 double]
uy: [6511×32 double]
Magnitude: [6511×32 double]
Plot the y-component of the solution for the fundamental frequency.
pdeplot(R.Mesh,XYData=R.ModeShapes.uy(:,1)) title(['First Mode with Frequency ', ... num2str(R.NaturalFrequencies(1)/(2*pi)),' Hz']) axis equal

Solve for the transient response at the center of a 3-D beam under a harmonic load on one of its corners.
Modal Analysis
Create a beam geometry.
gm = multicuboid(0.05,0.003,0.003);
Plot the geometry with the edge and vertex labels.
pdegplot(gm,EdgeLabels="on",VertexLabels="on"); view([95 5])

Create an femodel object for modal structural analysis and include the geometry.
model = femodel(AnalysisType="structuralModal", ... Geometry=gm);
Generate a mesh.
model = generateMesh(model);
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
model.MaterialProperties = ... materialProperties(YoungsModulus=210E9, ... PoissonsRatio=0.3, ... MassDensity=7800);
Specify minimal constraints on one end of the beam to prevent rigid body modes. For example, specify that edge 4 and vertex 7 are fixed boundaries.
model.EdgeBC(4) = edgeBC(Constraint="fixed"); model.VertexBC(7) = vertexBC(Constraint="fixed");
Solve the problem for the frequency range from 0 to 500,000. The recommended approach is to use a value that is slightly lower than the expected lowest frequency. Thus, use -0.1 instead of 0.
Rm = solve(model,FrequencyRange=[-0.1,500000]);
Transient Analysis
Switch the analysis type of the model to structural transient.
model.AnalysisType = "structuralTransient";Apply a sinusoidal force on the corner opposite of the constrained edge and vertex.
First, define a sinusoidal load function, sinusoidalLoad, to model a harmonic load. This function accepts the load magnitude (amplitude), the location and state structure arrays, frequency, and phase. Because the function depends on time, it must return a matrix of NaN of the correct size when state.time is NaN. Solvers check whether a problem is nonlinear or time-dependent by passing NaN state values and looking for returned NaN values.
function Tn = sinusoidalLoad(load,location,state,Frequency,Phase) if isnan(state.time) normal = [location.nx location.ny]; if isfield(location,"nz") normal = [normal location.nz]; end Tn = NaN*normal; return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Transient model excited with harmonic load Tn = load.*sin(Frequency.*state.time + Phase); end
Now, apply a sinusoidal force on vertex 5 by using the sinusoidalLoad function.
Force = [0,0,10];
Frequency = 7600;
Phase = 0;
forcePulse = @(location,state) ...
sinusoidalLoad(Force,location,state,Frequency,Phase);
model.VertexLoad(5) = vertexLoad(Force=forcePulse);Specify zero initial displacement and velocity.
model.CellIC = cellIC(Velocity=[0;0;0], ...
Displacement=[0;0;0]);Specify the relative and absolute tolerances for the solver.
model.SolverOptions.RelativeTolerance = 1E-5; model.SolverOptions.AbsoluteTolerance = 1E-9;
Solve the model using the modal results.
tlist = linspace(0,0.004,120); Rdm = solve(model,tlist,ModalResults=Rm);
Interpolate and plot the displacement at the center of the beam.
intrpUdm = interpolateDisplacement(Rdm,0,0,0.0015); plot(Rdm.SolutionTimes,intrpUdm.uz) grid on xlabel("Time"); ylabel("Center of beam displacement")

Solve a frequency response problem with damping. The resulting displacement values are complex. To obtain the magnitude and phase of displacement, use the abs and angle functions, respectively. To speed up computations, solve the model using the results of modal analysis.
Modal Analysis
Create a geometry representing a thin plate.
gm = multicuboid(10,10,0.025);
Create an femodel object for modal analysis and include the geometry in the model.
model = femodel(AnalysisType="structuralModal", ... Geometry=gm);
Generate a mesh.
model = generateMesh(model);
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
model.MaterialProperties = ... materialProperties(YoungsModulus=2E11, ... PoissonsRatio=0.3, ... MassDensity=8000);
Identify faces for applying boundary constraints and loads by plotting the geometry with the face and edge labels.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.5)
figure
pdegplot(model.Geometry,EdgeLabels="on",FaceAlpha=0.5)
Specify constraints on the sides of the plate (faces 3, 4, 5, and 6) to prevent rigid body motions.
model.FaceBC([3,4,5,6]) = faceBC(Constraint="fixed");Solve the problem for the frequency range from -Inf to 12*pi.
Rm = solve(model,FrequencyRange=[-Inf,12*pi]);
Frequency Response Analysis
Switch the analysis type of the model to frequency response.
model.AnalysisType = "structuralFrequency";Specify the pressure loading on top of the plate (face 2) to model an ideal impulse excitation. In the frequency domain, this pressure pulse is uniformly distributed across all frequencies.
model.FaceLoad(2) = faceLoad(Pressure=1E2);
First, solve the problem without damping.
flist = [0,1,1.5,linspace(2,3,100),3.5,4,5,6]*2*pi; RfrModalU = solve(model,flist,ModalResults=Rm);
Now, solve the problem with damping equal to 2% of critical damping for all modes.
RfrModalAll = solve(model,flist, ... ModalResults=Rm, ... DampingZeta=0.02);
Solve the same problem with frequency-dependent damping. In this example, use the solution frequencies from flist and damping values between 1% and 10% of critical damping.
omega = flist; zeta = linspace(0.01,0.1,length(omega)); zetaW = @(omegaMode) interp1(omega,zeta,omegaMode); RfrModalFD = solve(model,flist, ... ModalResults=Rm, ... DampingZeta=zetaW);
Interpolate the displacement at the center of the top surface of the plate for all three cases.
iDispU = interpolateDisplacement(RfrModalU,[0;0;0.025]); iDispAll = interpolateDisplacement(RfrModalAll,[0;0;0.025]); iDispFD = interpolateDisplacement(RfrModalFD,[0;0;0.025]);
Plot the magnitude of the displacement.
figure hold on plot(RfrModalU.SolutionFrequencies,abs(iDispU.Magnitude)); plot(RfrModalAll.SolutionFrequencies,abs(iDispAll.Magnitude)); plot(RfrModalFD.SolutionFrequencies,abs(iDispFD.Magnitude)); title("Magnitude")

Plot the phase of the displacement.
figure hold on plot(RfrModalU.SolutionFrequencies,angle(iDispU.Magnitude)); plot(RfrModalAll.SolutionFrequencies,angle(iDispAll.Magnitude)); plot(RfrModalFD.SolutionFrequencies,angle(iDispFD.Magnitude)); title("Phase")

Find the deflection of a 3-D cantilever beam under a nonuniform thermal load. Specify the thermal load for the structural problem using the solution from a transient thermal analysis on the same geometry and mesh.
Transient Thermal Model Analysis
Create and plot the geometry.
gm = multicuboid(0.5,0.1,0.05);
pdegplot(gm,FaceLabels="on",FaceAlpha=0.3)
Create an femodel object for transient thermal analysis and include the geometry.
model = femodel(AnalysisType="thermalTransient", ... Geometry = gm);
Generate a mesh.
model = generateMesh(model);
Specify the thermal properties of the material.
model.MaterialProperties = ... materialProperties(ThermalConductivity=5e-3, ... MassDensity=2.7*10^(-6), ... SpecificHeat=10);
Specify the constant temperatures applied to the left and right ends of the beam.
model.FaceBC(3) = faceBC(Temperature=100); model.FaceBC(5) = faceBC(Temperature=0);
Specify the heat source over the entire geometry.
model.CellLoad = cellLoad(Heat=10);
Set the initial temperature.
model.CellIC = cellIC(Temperature=0);
Solve the model.
tlist = 0:1e-4:2e-4; thermalresults = solve(model,tlist);
Plot the temperature distribution for each time step.
for n = 1:numel(thermalresults.SolutionTimes) figure pdeplot3D(thermalresults.Mesh, ... ColorMapData=thermalresults.Temperature(:,n)) title(["Temperature at Time = " ... num2str(tlist(n))]) end
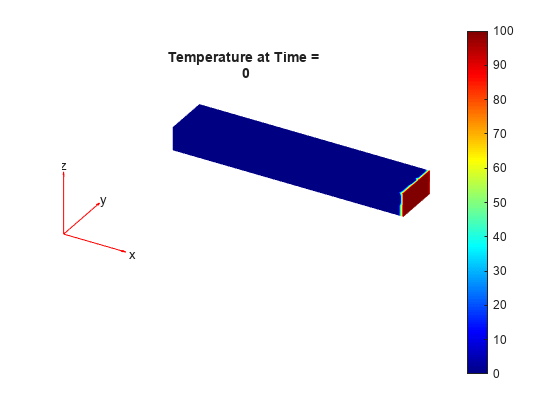


Structural Analysis with Thermal Load
Switch the analysis type of the model to structural static.
model.AnalysisType = "structuralStatic";Specify Young's modulus, Poisson's ratio, and the coefficient of thermal expansion.
model.MaterialProperties = ... materialProperties(YoungsModulus=1e10, ... PoissonsRatio=0.3, ... CTE=11.7e-6);
Apply a fixed boundary condition on face 5.
model.FaceBC(5) = faceBC(Constraint="fixed");Apply a thermal load using the transient thermal results. By default, the toolbox uses the solution for the last time step.
model.CellLoad = cellLoad(Temperature=thermalresults);
Specify the reference temperature.
model.ReferenceTemperature = 10;
Solve the structural problem.
thermalstressresults = solve(model);
Plot the deformed shape of the beam corresponding to the last step of the transient thermal solution.
pdeplot3D(thermalstressresults.Mesh, ... "ColorMapData", ... thermalstressresults.Displacement.Magnitude, ... "Deformation", ... thermalstressresults.Displacement) title(["Thermal Expansion at Solution Time = " ... num2str(tlist(end))])

Now specify the thermal loads as the thermal results for all time steps. Access the results for each step by using the filterByIndex function. For each thermal load, solve the structural problem and plot the corresponding deformed shape of the beam.
for n = 1:numel(thermalresults.SolutionTimes) resultsByStep = filterByIndex(thermalresults,n); model.CellLoad = ... cellLoad(Temperature=resultsByStep); thermalstressresults = solve(model); figure pdeplot3D(thermalstressresults.Mesh, ... ColorMapData = ... thermalstressresults.Displacement.Magnitude, ... Deformation = ... thermalstressresults.Displacement) title(["Thermal Results at Solution Time = " ... num2str(tlist(n))]) end



Solve a 3-D steady-state thermal problem.
Create an femodel object for a steady-state thermal problem and include a geometry representing a block.
model = femodel(AnalysisType="thermalSteady", ... Geometry="Block.stl");
Plot the block geometry.
pdegplot(model.Geometry, ... FaceLabels="on", ... FaceAlpha=0.5) axis equal

Assign material properties.
model.MaterialProperties = ...
materialProperties(ThermalConductivity=80);Apply a constant temperature of 100 °C to the left side of the block (face 1) and a constant temperature of 300 °C to the right side of the block (face 3). All other faces are insulated by default.
model.FaceBC(1) = faceBC(Temperature=100); model.FaceBC(3) = faceBC(Temperature=300);
Mesh the geometry and solve the problem.
model = generateMesh(model); thermalresults = solve(model)
thermalresults =
SteadyStateThermalResults with properties:
Temperature: [12822×1 double]
XGradients: [12822×1 double]
YGradients: [12822×1 double]
ZGradients: [12822×1 double]
Mesh: [1×1 FEMesh]
The solver finds the temperatures and temperature gradients at the nodal locations. To access these values, use thermalresults.Temperature, thermalresults.XGradients, and so on. For example, plot temperatures at the nodal locations.
pdeplot3D(thermalresults.Mesh,ColorMapData=thermalresults.Temperature)

Solve a 2-D transient thermal problem.
Create a geometry representing a square plate with a diamond-shaped region in its center.
SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3]; D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5]; gd = [SQ1 D1]; sf = 'SQ1+D1'; ns = char('SQ1','D1'); ns = ns'; g = decsg(gd,sf,ns); pdegplot(g,EdgeLabels="on",FaceLabels="on") xlim([-1.5 4.5]) ylim([-0.5 3.5]) axis equal

Create an femodel object for transient thermal analysis and include the geometry.
model = femodel(AnalysisType="thermalTransient", ... Geometry=g);
For the square region, assign these thermal properties:
Thermal conductivity is
Mass density is
Specific heat is
model.MaterialProperties(1) = ... materialProperties(ThermalConductivity=10, ... MassDensity=2, ... SpecificHeat=0.1);
For the diamond region, assign these thermal properties:
Thermal conductivity is
Mass density is
Specific heat is
model.MaterialProperties(2) = ... materialProperties(ThermalConductivity=2, ... MassDensity=1, ... SpecificHeat=0.1);
Assume that the diamond-shaped region is a heat source with a density of .
model.FaceLoad(2) = faceLoad(Heat=4);
Apply a constant temperature of 0 °C to the sides of the square plate.
model.EdgeBC(1:4) = edgeBC(Temperature=0);
Set the initial temperature to 0 °C.
model.FaceIC = faceIC(Temperature=0);
Generate the mesh.
model = generateMesh(model);
The dynamics for this problem are very fast. The temperature reaches a steady state in about 0.1 second. To capture the most active part of the dynamics, set the solution time to logspace(-2,-1,10). This command returns 10 logarithmically spaced solution times between 0.01 and 0.1.
tlist = logspace(-2,-1,10);
Solve the equation.
thermalresults = solve(model,tlist);
Plot the solution with isothermal lines by using a contour plot.
T = thermalresults.Temperature; msh = thermalresults.Mesh; pdeplot(msh,XYData=T(:,10),Contour="on",ColorMap="hot") axis equal

Solve a transient thermal problem by first obtaining mode shapes for a particular decay range and then using the modal superposition method.
Modal Decomposition
Create a geometry representing a square plate with a diamond-shaped region in its center.
SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3]; D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5]; gd = [SQ1 D1]; sf = 'SQ1+D1'; ns = char('SQ1','D1'); ns = ns'; g = decsg(gd,sf,ns); pdegplot(g,EdgeLabels="on",FaceLabels="on") xlim([-1.5 4.5]) ylim([-0.5 3.5]) axis equal

Create an femodel object for modal thermal analysis and include the geometry.
model = femodel(AnalysisType="thermalModal", ... Geometry=g);
For the square region, assign these thermal properties:
Thermal conductivity is .
Mass density is .
Specific heat is .
model.MaterialProperties(1) = ... materialProperties(ThermalConductivity=10, ... MassDensity=2, ... SpecificHeat=0.1);
For the diamond region, assign these thermal properties:
Thermal conductivity is .
Mass density is .
Specific heat is .
model.MaterialProperties(2) = ... materialProperties(ThermalConductivity=2, ... MassDensity=1, ... SpecificHeat=0.1);
Assume that the diamond-shaped region is a heat source with a density of .
model.FaceLoad(2) = faceLoad(Heat=4);
Apply a constant temperature of 0 °C to the sides of the square plate.
model.EdgeBC(1:4) = edgeBC(Temperature=0);
Set the initial temperature to 0 °C.
model.FaceIC = faceIC(Temperature=0);
Generate the mesh.
model = generateMesh(model);
Compute eigenmodes of the model in the decay range [100,10000] .
RModal = solve(model,DecayRange=[100,10000])
RModal =
ModalThermalResults with properties:
DecayRates: [164×1 double]
ModeShapes: [1461×164 double]
ModeType: "EigenModes"
Mesh: [1×1 FEMesh]
Transient Analysis
Knowing the mode shapes, you can now use the modal superposition method to solve the transient thermal problem. First, switch the model analysis type to thermal transient.
model.AnalysisType = "thermalTransient";The dynamics for this problem are very fast. The temperature reaches a steady state in about 0.1 second. To capture the most active part of the dynamics, set the solution time to logspace(-2,-1,100). This command returns 100 logarithmically spaced solution times between 0.01 and 0.1.
tlist = logspace(-2,-1,10);
Solve the equation.
Rtransient = solve(model,tlist,ModalResults=RModal);
Plot the solution with isothermal lines by using a contour plot.
msh = Rtransient.Mesh
msh =
FEMesh with properties:
Nodes: [2×1461 double]
Elements: [6×694 double]
MaxElementSize: 0.1697
MinElementSize: 0.0849
MeshGradation: 1.5000
GeometricOrder: 'quadratic'
T = Rtransient.Temperature; pdeplot(msh,XYData=T(:,end),Contour="on", ... ColorMap="hot") axis equal

Obtain POD modes of a linear thermal problem using several instances of the transient solution (snapshots).
Create an femodel object for transient thermal analysis and include a unit square geometry in the model.
model = femodel(AnalysisType="thermalTransient", ... Geometry=@squareg);
Plot the geometry, displaying edge labels.
pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])
Specify the thermal conductivity, mass density, and specific heat of the material.
model.MaterialProperties = ... materialProperties(ThermalConductivity=400, ... MassDensity=1300, ... SpecificHeat=600);
Set the temperature on the right edge to 100.
model.EdgeBC(2) = edgeBC(Temperature=100);
Set an initial value of 0 for the temperature.
model.FaceIC = faceIC(Temperature=0);
Generate a mesh.
model = generateMesh(model);
Solve the model for three different values of heat source and collect snapshots.
tlist = 0:10:600; snapShotIDs = [1:10 59 60 61]; Tmatrix = []; heatVariation = [10000 15000 20000]; for q = heatVariation model.FaceLoad = faceLoad(Heat=q); results = solve(model,tlist); Tmatrix = [Tmatrix,results.Temperature(:,snapShotIDs)]; end
Switch the model analysis type to thermal modal.
model.AnalysisType = "thermalModal";Compute the POD modes.
RModal = solve(model,Snapshots=Tmatrix)
RModal =
ModalThermalResults with properties:
DecayRates: [6×1 double]
ModeShapes: [1529×6 double]
SnapshotsAverage: [1529×1 double]
ModeType: "PODModes"
Mesh: [1×1 FEMesh]
Solve an electromagnetic problem and find the electric potential and field distribution for a 2-D geometry representing a plate with a hole.
Create an femodel object for electrostatic analysis and include a geometry representing a plate with a hole.
model = femodel(AnalysisType="electrostatic",... Geometry="PlateHolePlanar.stl");
Plot the geometry with edge labels.
pdegplot(model.Geometry,EdgeLabels="on")
Specify the vacuum permittivity value in the SI system of units.
model.VacuumPermittivity = 8.8541878128E-12;
Specify the relative permittivity of the material.
model.MaterialProperties = ...
materialProperties(RelativePermittivity=1);Apply the voltage boundary conditions on the edges framing the rectangle and the circle.
model.EdgeBC(1:4) = edgeBC(Voltage=0); model.EdgeBC(5) = edgeBC(Voltage=1000);
Specify the charge density for the entire geometry.
model.FaceLoad = faceLoad(ChargeDensity=5E-9);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model)
R =
ElectrostaticResults with properties:
ElectricPotential: [1231×1 double]
ElectricField: [1×1 FEStruct]
ElectricFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
Plot the electric potential distribution using the Contour parameter to display equipotential lines and the Levels parameter to specify how many equipotential lines to display.
pdeplot(R.Mesh,XYData=R.ElectricPotential, ... Contour="on", ... Levels=5) axis equal

You can also use the Levels parameter to specify electric potential values for which to display equipotential lines.
pdeplot(R.Mesh,XYData=R.ElectricPotential, ... Contour="on", ... Levels=[500 1500 2500 4000]) axis equal
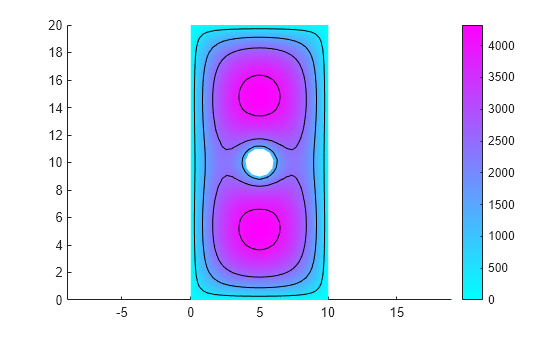
Now plot the electric potential, the equipotential line for the potential value 750, and a quiver plot representing the electric field.
pdeplot(R.Mesh,XYData=R.ElectricPotential, ... Contour="on", ... Levels=[750 750], ... FlowData=[R.ElectricField.Ex ... R.ElectricField.Ey]) axis equal
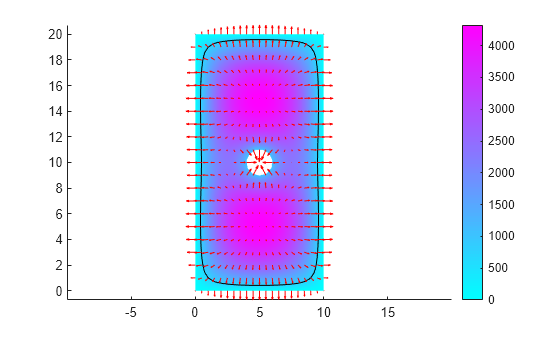
Solve a 3-D electromagnetic problem on a geometry representing a plate with a hole in its center. Plot the resulting magnetic potential and field distribution.
Create an femodel object for magnetostatic analysis and include a geometry representing a plate with a hole.
model = femodel(AnalysisType="magnetostatic", ... Geometry="PlateHoleSolid.stl");
Plot the geometry.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)
Specify the vacuum permeability value in the SI system of units.
model.VacuumPermeability = 1.2566370614e-6;
Specify the relative permeability of the material.
model.MaterialProperties = ...
materialProperties(RelativePermeability=5000);Apply the magnetic potential boundary conditions on the side faces and the face bordering the hole.
model.FaceBC(3:6) = faceBC(MagneticPotential=[0;0;0]); model.FaceBC(7) = faceBC(MagneticPotential=[0;0;0.01]);
Specify the current density for the entire geometry.
model.CellLoad = cellLoad(CurrentDensity=[0;0;0.5]);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model)
R =
MagnetostaticResults with properties:
MagneticPotential: [1×1 FEStruct]
MagneticField: [1×1 FEStruct]
MagneticFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
Plot the z-component of the magnetic potential.
pdeplot3D(R.Mesh,ColormapData=R.MagneticPotential.Az)

Plot the magnetic field.
pdeplot3D(R.Mesh,FlowData=[R.MagneticField.Hx ... R.MagneticField.Hy ... R.MagneticField.Hz])

Solve a DC conduction problem on a geometry representing a 3-D plate with a hole in its center. Plot the electric potential and the components of the current density.
Create an femodel object for DC conduction analysis and include a geometry representing a plate with a hole.
model = femodel(AnalysisType="dcConduction", ... Geometry="PlateHoleSolid.stl");
Plot the geometry.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)
Specify the conductivity of the material.
model.MaterialProperties = ...
materialProperties(ElectricalConductivity=6e4);Apply the voltage boundary conditions on the left, right, top, and bottom faces of the plate.
model.FaceBC(3:6) = faceBC(Voltage=0);
Specify the surface current density on the face bordering the hole.
model.FaceLoad(7) = faceLoad(SurfaceCurrentDensity=100);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model)
R =
ConductionResults with properties:
ElectricPotential: [4747×1 double]
ElectricField: [1×1 FEStruct]
CurrentDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
Plot the electric potential.
figure pdeplot3D(R.Mesh,ColorMapData=R.ElectricPotential)

Plot the x-component of the current density.
figure
pdeplot3D(R.Mesh,ColorMapData=R.CurrentDensity.Jx)
title("x-Component of Current Density")
Plot the y-component of the current density.
figure
pdeplot3D(R.Mesh,ColorMapData=R.CurrentDensity.Jy)
title("y-Component of Current Density")
Plot the z-component of the current density.
figure
pdeplot3D(R.Mesh,ColorMapData=R.CurrentDensity.Jz)
title("z-Component of Current Density")
Use a solution obtained by performing a DC conduction analysis to specify current density for a magnetostatic problem.
Create an femodel object for DC conduction analysis and include a geometry representing a plate with a hole.
model = femodel(AnalysisType="dcConduction", ... Geometry="PlateHoleSolid.stl");
Plot the geometry.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)
Specify the conductivity of the material.
model.MaterialProperties = ...
materialProperties(ElectricalConductivity=6e4);Apply the voltage boundary conditions on the left, right, top, and bottom faces of the plate.
model.FaceBC(3:6) = faceBC(Voltage=0);
Specify the surface current density on the face bordering the hole.
model.FaceLoad(7) = faceLoad(SurfaceCurrentDensity=100);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model);
Change the analysis type of the model to magnetostatic.
model.AnalysisType = "magnetostatic";This model already has a quadratic mesh that you generated for the DC conduction analysis. For a 3-D magnetostatic model, the mesh must be linear. Generate a new linear mesh. The generateMesh function creates a linear mesh by default if the model is 3-D and magnetostatic.
model = generateMesh(model);
Specify the vacuum permeability value in the SI system of units.
model.VacuumPermeability = 1.2566370614e-6;
Specify the relative permeability of the material.
model.MaterialProperties = ...
materialProperties(RelativePermeability=5000);Apply the magnetic potential boundary conditions on the side faces and the face bordering the hole.
model.FaceBC(3:6) = faceBC(MagneticPotential=[0;0;0]); model.FaceBC(7) = faceBC(MagneticPotential=[0;0;0.01]);
Specify the current density for the entire geometry using the DC conduction solution.
model.CellLoad = cellLoad(CurrentDensity=R);
Solve the problem.
Rmagnetostatic = solve(model);
Plot the x- and z-components of the magnetic potential.
pdeplot3D(Rmagnetostatic.Mesh, ...
ColormapData=Rmagnetostatic.MagneticPotential.Ax)
pdeplot3D(Rmagnetostatic.Mesh, ...
ColormapData=Rmagnetostatic.MagneticPotential.Az)
Solve a magnetostatic problem of a copper square with a permanent neodymium magnet in its center.
Create the unit square geometry with a circle in its center.
L = 0.8; r = 0.25; sq = [3 4 -L L L -L -L -L L L]'; circ = [1 0 0 r 0 0 0 0 0 0]'; gd = [sq,circ]; sf = "sq + circ"; ns = char('sq','circ'); ns = ns'; g = decsg(gd,sf,ns);
Plot the geometry with the face and edge labels.
pdegplot(g,FaceLabels="on",EdgeLabels="on")

Create an femodel object for magnetostatic analysis and include the geometry in the model.
model = femodel(AnalysisType="magnetostatic", ... Geometry=g);
Specify the vacuum permeability value in the SI system of units.
model.VacuumPermeability = 1.2566370614e-6;
Specify the relative permeability of the copper for the square.
model.MaterialProperties(1) = ...
materialProperties(RelativePermeability=1);Specify the relative permeability of the neodymium for the circle.
model.MaterialProperties(2) = ...
materialProperties(RelativePermeability=1.05);Specify the magnetization magnitude for the neodymium magnet.
M = 1e6;
Specify magnetization on the circular face in the positive x-direction. Magnetization for a 2-D model is a column vector of two elements.
dir = [1;0]; model.FaceLoad(2) = faceLoad(Magnetization=M*dir);
Apply the magnetic potential boundary conditions on the edges framing the square.
model.EdgeBC(1:4) = edgeBC(MagneticPotential=0);
Generate the mesh with finer meshing near the edges of the circle.
model = generateMesh(model,Hedge={5:8,0.007});
figure
pdemesh(model)
Solve the problem, and find the resulting magnetic fields B and H. Here, , where is the absolute magnetic permeability of the material, is the vacuum permeability, and is the magnetization.
R = solve(model); Bmag = sqrt(R.MagneticFluxDensity.Bx.^2 + R.MagneticFluxDensity.By.^2); Hmag = sqrt(R.MagneticField.Hx.^2 + R.MagneticField.Hy.^2);
Plot the magnetic field B.
figure pdeplot(R.Mesh,XYData=Bmag, ... FlowData=[R.MagneticFluxDensity.Bx ... R.MagneticFluxDensity.By]) axis equal

Plot the magnetic field H.
figure pdeplot(R.Mesh,XYData=Hmag, ... FlowData=[R.MagneticField.Hx R.MagneticField.Hy]) axis equal

For an electromagnetic harmonic analysis problem, find the x- and y-components of the electric field. Solve the problem on a domain consisting of a square with a circular hole.
For the geometry, define a circle in a square, place them in one matrix, and create a set formula that subtracts the circle from the square.
SQ = [3,4,-5,-5,5,5,-5,5,5,-5]';
C = [1,0,0,1]';
C = [C;zeros(length(SQ) - length(C),1)];
gm = [SQ,C];
sf = 'SQ-C';Create the geometry.
ns = char('SQ','C'); ns = ns'; g = decsg(gm,sf,ns);
Create an femodel object for electromagnetic harmonic analysis with an electric field type. Include the geometry in the model.
model = femodel(AnalysisType="electricHarmonic", ... Geometry=g);
Plot the geometry with the edge labels.
pdegplot(model.Geometry,EdgeLabels="on")
xlim([-5.5 5.5])
ylim([-5.5 5.5])
Specify the vacuum permittivity and permeability values as 1.
model.VacuumPermittivity = 1; model.VacuumPermeability = 1;
Specify the relative permittivity, relative permeability, and conductivity of the material.
model.MaterialProperties = ... materialProperties(RelativePermittivity=1, ... RelativePermeability=1, ... ElectricalConductivity=0);
Apply the absorbing boundary condition with a thickness of 2 on the edges of the square. Use the default attenuation rate for the absorbing region.
ffbc = farFieldBC(Thickness=2); model.EdgeBC(1:4) = edgeBC(FarField=ffbc);
Specify an electric field on the edges of the hole.
E = @(location,state) [1;0]*exp(-1i*2*pi*location.y); model.EdgeBC(5:8) = edgeBC(ElectricField=E);
Generate a mesh.
model = generateMesh(model,Hmax=1/2^3);
Solve the model for a frequency of .
result = solve(model,2*pi);
Plot the real part of the x-component of the resulting electric field.
figure pdeplot(result.Mesh,XYData=real(result.ElectricField.Ex)); title("Real Part of x-Component of Electric Field") axis equal

Plot the real part of the y-component of the resulting electric field.
figure pdeplot(result.Mesh,XYData=real(result.ElectricField.Ey)); title("Real Part of y-Component of Electric Field") axis equal

Input Arguments
Finite element analysis model, specified as an femodel object. The model contains information about a finite
element problem: analysis type, geometry, material properties, boundary
conditions, loads, initial conditions, and other parameters. Depending on
the analysis type, it represents a structural, thermal, or electromagnetic
problem.
Example: model = femodel(AnalysisType =
"structuralStatic")
Solution times for structural or thermal transient analysis, specified as a real vector of monotonically increasing or decreasing values.
Example: 0:20
Data Types: double
Solution frequencies for a frequency response structural analysis, specified as a real vector of monotonically increasing or decreasing values.
Example: linspace(0,4000,150)
Data Types: double
Frequency range for a structural modal analysis, specified as a vector of
two elements. Define omega1 as slightly lower than the
lowest expected frequency and omega2 as slightly higher
than the highest expected frequency. For example, if the lowest expected
frequency is zero, then use a small negative value for
omega1.
Example: [-0.1,1000]
Data Types: double
Modal analysis results for a structural model, specified as a
ModalStructuralResults object.
Example: structuralModalR =
solve(structuralmodel,FrequencyRange=[0,1e6])
Decay range for modal thermal analysis, specified as a vector of two
elements. The solve function solves a modal thermal
analysis model for all modes in the decay range.
Data Types: double
Thermal model solution snapshots, specified as a matrix.
Data Types: double
Modal analysis results for a thermal model, specified as a
ModalThermalResults object.
Example: thermalModalR =
solve(thermalmodel,DecayRange=[0,1000])
Modal damping ratio, specified as a nonnegative number or a function handle. Use a function handle when each mode has its own damping ratio. The function must accept a vector of natural frequencies as an input argument and return a vector of corresponding damping ratios. It must cover the full frequency range for all modes used for modal solution. For details, see Modal Damping Depending on Frequency.
Data Types: double | function_handle
Solution frequencies for a harmonic electromagnetic analysis, specified as a nonnegative number or a vector of nonnegative numbers.
Data Types: double
Output Arguments
Structural, thermal, or electromagnetic analysis results, returned as a
StaticStructuralResults, TransientStructuralResults, FrequencyStructuralResults, ModalStructuralResults, SteadyStateThermalResults, TransientThermalResults, ModalThermalResults, ElectrostaticResults, MagnetostaticResults, ConductionResults, or HarmonicResults object.
Tips
When you use modal analysis results to solve a transient structural dynamics model, the
modalresultsargument must be created in Partial Differential Equation Toolbox™ from R2019a or newer.For a frequency response model with damping, the results are complex. Use functions such as
absandangleto obtain real-valued results, such as the magnitude and phase.
Version History
Introduced in R2017asolve will no longer accept StructuralModel,
ThermalModel, and ElectromagneticModel.
These objects will be removed. Use an femodel
object instead.
The unified finite element model workflow defines the type of a problem and all of
its parameters as the properties of an femodel object. This
object enables you to specify physical parameters for structural, thermal, and
electromagnetic types of analyses. The solver in the unified workflow uses only the
parameters (properties) appropriate for the current analysis type while ignoring all
other properties. If you switch the analysis type by setting the
AnalysisType property of the model, the solver uses the
appropriate set of properties corresponding to the new analysis type.
For more help migrating your existing code that uses
StructuralModel, ThermalModel, or
ElectromagneticModel to the unified finite element workflow,
see Migration from Domain-Specific to Unified Workflow.
The solver accepts the femodel
object that defines structural mechanics, thermal, and electromagnetic
problems.
You can now solve stationary current distribution in conductors due to applied voltage. You also can solve electromagnetic problems accounting for magnetization of materials.
You can now solve 2-D and 3-D time-harmonic Maxwell’s equations (the Helmholtz equation).
You can now compute modes of a thermal model using eigenvalue or proper orthogonal decomposition. You also can speed up computations for a transient thermal model by using the computed modes.
You can now solve 3-D electrostatic and magnetostatic problems.
You can now solve 2-D electrostatic and magnetostatic problems.
You can now solve axisymmetric structural and thermal problems. Axisymmetric analysis simplifies 3-D thermal problems to 2-D using their symmetry around the axis of rotation.
You can now solve frequency response structural problems and find displacement,
velocity, acceleration, and solution frequencies at nodal locations of the mesh. To
speed up computations, you can use modal analysis results for frequency response
analysis. The ModalResults argument triggers the
solve function to use the modal superposition method.
You can now specify the maximum number of Lanczos shifts and the block size for
block Lanczos recurrence by using the SolverOptions property of
StructuralModel. For details, see PDESolverOptions Properties.
The new ModalResults argument triggers the
solve function to switch to the modal transient solver
instead of using the direct integration approach.
The solver now solves accounts for mechanical and thermal effects when solving a static structural analysis model. The function returns a displacement, stress, strain, and von Mises stress induced by both mechanical and thermal loads.
You can now solve dynamic linear elasticity problems and find displacement, velocity, and acceleration at nodal locations of the mesh.
You also can solve modal analysis problems and find natural frequencies and mode shapes of a structure. When solving a modal analysis model, the solver requires a frequency range parameter and returns the modal solution in that frequency range.
You can now solve static linear elasticity problems and find displacement, stress, strain, and von Mises stress at nodal locations of the mesh.
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)