framesig
Syntax
Description
Examples
Create a matrix signal x and split each channel into frames of length 5 with 3 samples of overlap between consecutive frames.
x = reshape(1:24,12,2); [xw,fc,fi] = framesig(x,5,OverlapLength=3)
xw =
xw(:,:,1) =
1 3 5 7
2 4 6 8
3 5 7 9
4 6 8 10
5 7 9 11
xw(:,:,2) =
13 15 17 19
14 16 18 20
15 17 19 21
16 18 20 22
17 19 21 23
fc = 4×2
9 21
10 22
11 23
12 24
fi = 1
Since x has two columns, xw results a 3-D matrix representing two channels of four frames and five samples per frame. The last three samples on any given frame are overlapped in the next one. fc contains the samples from the incomplete fifth frame in each channel, including the overlapping samples. fi is 1 due to the specified overlap length.
Compute the power spectral density of a signal by partitioning it into frames, windowing each frame, and applying the fast Fourier transform to each windowed frame.
Generate a signal x as 200-Hz cosine waveform with normally distributed noise. Set a sampling rate of 1000 samples per second and a time limit of 0.3 seconds.
fs = 1000; t = 0:1/fs:0.3; x = cos(2*pi*200*t)+randn(size(t));
Frame the signal using framesig with a frame length of 66 samples. Specify a Hamming window and 33 samples of overlap.
fl = 66; ol = 33; g = hamming(fl); xw = framesig(x,fl,Window=g,OverlapLength=ol);
Compute the power spectral density. Use 256 points to compute the discrete Fourier transform for the framed signal.
NFFT = 256; X = fft(xw,NFFT); S = (diag(X*X')/(g'*g))/(size(xw,2)*fs);
Compare the computed power spectral density with Welch’s power spectral density estimate.
[p,f] = pwelch(x,fl,ol,NFFT,fs,"twosided"); plot(f,pow2db(p),f,pow2db(S),"--") xlabel("Frequency (Hz)") ylabel("Power/Frequency (dB/Hz)") legend(["pwelch" "fft"]) grid

Create a multivariable single-channel timetable input signal and an initial condition timetable.
xTT = timetable(seconds((1:20)'),(1:20)',(41:60)'); icTT = timetable(seconds((-2:0)'),(-2:0)',(38:40)');
Split each variable into frames of length 4, using an underlap length of 3, an initial condition timetable, and setting the property IncompleteFrameRule to "zeropad".
xwTT = framesig(xTT,4,UnderlapLength=3, ... InitialCondition=icTT,IncompleteFrameRule="zeropad")
xwTT=4×2 timetable
Time Var1 Var2
________ ____________________ ____________________
-0.5 sec -2 -1 0 1 38 39 40 41
6.5 sec 5 6 7 8 45 46 47 48
13.5 sec 12 13 14 15 52 53 54 55
20.5 sec 19 20 0 0 59 60 0 0
Generate a 3-D signal array, define a 3-D initial condition array, and partition the signal array along its third dimension.
Define a 3-D array with 30 elements from 1 to 30, distributed along two rows, three columns, and five pages.
x = reshape(1:30,[2 3 5]);
Set an initial-condition array as a 3-D array with 12 elements from –11 to 0, distributed along two rows, three columns, and two pages.
initCond = reshape(-11:0,[2,3,2]);
Partition the signal array along its third dimension. Display the first page of the framed signal output.
[xw,fc] = framesig(x,3,OverlapLength=2, ...
InitialCondition=initCond,Dimension=3);
disp(xw(:,:,1,:))(:,:,1,1) =
-11 -5 1 7 13
-5 1 7 13 19
1 7 13 19 25
(:,:,1,2) =
-9 -3 3 9 15
-3 3 9 15 21
3 9 15 21 27
(:,:,1,3) =
-7 -1 5 11 17
-1 5 11 17 23
5 11 17 23 29
Define a multisegment data stream signal, perform successive framing for each segment, and compare with the framing of the entire stream.
Define a signal source stream data in two segments with a length of 7 samples per segment.
Ls = 7; x0 = (1:2*Ls)'; x = reshape(x0,Ls,[]);
Split each segment into frames of length 4 with 3 samples of overlap between frames. Set the initial condition as an empty vector.
fl = 4; ol = 3; ic0 = [];
Perform successive framing of the data stream signal. Initialize the output frames and the initial condition array. Frame each segment with the specified frame length, overlap length, and initial condition. Keep the same amount of overlap among frames of consecutive segments. Accumulate the output frames after each iteration. Display the output frames and the final condition array.
xwa = []; ici = ic0; numSegments = size(x,2); for i = 1:numSegments % Data streaming and framing xi = x(:,i); [xwi,fci] = framesig(xi,fl,OverlapLength=ol, ... InitialCondition=ici); % Settings for the next iteration xwa = [xwa xwi]; ici = fci; end disp(xwa)
1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 13
4 5 6 7 8 9 10 11 12 13 14
disp(fci)
12
13
14
Frame the entire data stream with the specified frame length, overlap length, and initial condition. Observe that successive overlap framing yields the same result as when you feed all the segments at once.
[xwe,fce] = framesig(x0,fl,OverlapLength=ol, ...
InitialCondition=ic0)xwe = 4×11
1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 13
4 5 6 7 8 9 10 11 12 13 14
fce = 3×1
12
13
14
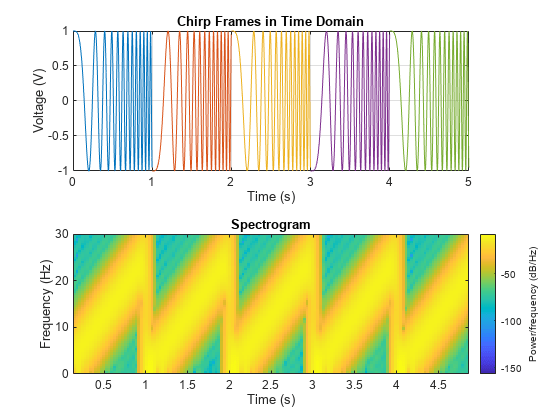
Use the framesig and chirp functions to generate a linearly swept-frequency cosine signal in each frame.
Specify a time vector representing five periods of 1 second, with a sample rate of 500 Hz.
Fs = 500; T0 = 1; t = (0:1/Fs:5*T0-1/Fs)';
Define the frame length as the number of samples in one single period.
fl = round(T0*Fs);
Partition a time vector into frames.
tf = framesig(t,fl);
Generate a linear swept-frequency cosine signal at the time instances defined in each frame. Set the reference frequencies so that the chirp instantaneous frequency starts at 0 Hz and crosses 25 Hz at the end of the period T0. Specify the sweep method option as "linear". Alternate the signs for all even frames.
f0 = 0; f1 = 25; numFrames = size(tf,2); y = zeros(fl,numFrames); for i = 1:numFrames tfi = mod(tf(:,i),T0); y(:,i) = chirp(tfi,f0,T0,f1,"linear")*(-1)^(i-1); end
Plot the chirp signal frames in time domain. Plot the spectrogram of the entire stream. Use a 144-sample Blackman window, an overlap of 128 samples, 1024 sampling points to calculate the discrete Fourier transform, the signal sampling frequency Fs, and set the frequency display axis property to "yaxis".
tiledlayout flow nexttile plot(tf,y) title("Chirp Frames in Time Domain") xlabel("Time (s)") ylabel("Voltage (V)") grid nexttile spectrogram(y(:),blackman(144),128,1024,Fs,"yaxis") title("Spectrogram") xlabel("Time (s)") ylabel("Frequency (Hz)") ylim([f0 1.2*f1])
Partition a data stream signal into segments using overlap. Perform successive framing and joint framing of the signal segments with underlap.
Load a data file with a 73113-sample signal y sampled at a rate Fs of 8192 Hz.
load handelOverlap Framing into Segments
Partition a signal y into 25000-sample segments. Specify an overlap length of 5000 samples, pad the last frame with zeros if incomplete, and set as initial condition a column vector with 5000 zeros. Plot the data frames. Highlight the overlapping regions between frames.
sl = 25000; ol = 5000; yfs = framesig(y,sl,OverlapLength=ol, ... IncompleteFrameRule="zeropad", ... InitialCondition=zeros(ol,1)); ns = size(yfs,2); strips(yfs) patch([0 sl]+[1 -1].*[0 0 ol ol]',2*([-1 0]+[1 ns ns 1]')-1, ... "r",EdgeColor="none",FaceAlpha=0.1) grid xlabel("Sample Number") ylabel("Segment Number") yticklabels(ns:-1:1)

The plot shows that:
The signal partition delivers four segments.
The first
olsamples in the first segment are zeros because of the initial condition.The last
olsamples in each segment repeat in the next frame due to the specified overlap length.Since the framing operation has a zero-padding rule, the last segment includes the last samples of
yand completes with zeros.
Successive Underlap Framing
Perform successive underlap framing of a segmented data stream matrix. Specify a frame length of 256 samples and an underlap length of 112 samples. Frame each segment with the specified frame length, underlap length, initial condition, and initial index. Concatenate the output frames after each framing iteration. Keep the same amount of underlap among frames of consecutive segments.
fl = 256; ul = 112; yfa = []; ic0 = []; ii0 = 1; ica = ic0; iia = ii0; for i = 1:ns % Data streaming and framing yi = yfs(:,i); [yfi,fci,fii] = framesig(yi,fl,UnderlapLength=ul, ... InitialCondition=ica,InitialIndex=iia); disp("i = "+i+", fii = "+fii) % Settings for the next iteration yfa = [yfa yfi]; ica = fci; iia = fii; end
i = 1, fii = 25 i = 2, fii = 49 i = 3, fii = 73 i = 4, fii = 97
The framing of first 25000-sample segment outputs from sample 1 through 256, then from sample 369 through 624, and so on until the last complete frame, from sample 24657 through 24912. Since the underlap length is 112 samples and the incomplete frame rule is "drop" (default value), the framing operation skips and counts from sample 24912 to 25000, casting 88 samples. The final index output fii sets to 25 since fii-1 is the difference between the 112 underlapping samples and the 88 samples skipped after the last complete frame. The framing of the next 25000-sample segments outputs final index outputs as 49, 73, and 97.
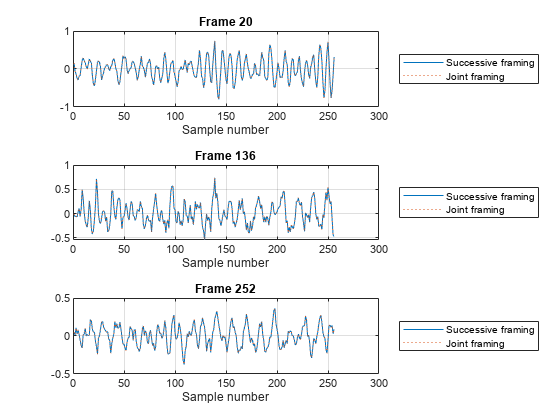
Joint Underlap Framing
Frame the entire segmented data stream with the specified frame length, overlap length, and initial condition. Plot the 20th, central, and 20th-last frames. Observe that successive underlap framing yields the same result as when you feed all the segments at once.
[yfe,fce,fie] = framesig(yfs(:),fl,UnderlapLength=ul, ... InitialCondition=ic0,InitialIndex=ii0); nf = size(yfe,2); figure tiledlayout vertical for i = [20 floor(nf/2) nf-20] nexttile plot(yfa(:,i)) hold on plot(yfe(:,i),":") hold off grid xlabel("Sample number") title("Frame "+i) legend(["Successive" "Joint"]+" framing",Location="eastoutside") end
Input Arguments
Input signal, specified as a vector, matrix, N-D array,
timetable, or unformatted dlarray object.
Vector — the output
xwis anfl-by-NF matrix where NF is the number of frames.Matrix —
framesigtreats each column ofxas an independent channel. The output is a 3-D array of sizefl-by-NF-by-NC, where NC is the number of channels.N-D array —
framesig:Permutes the array dimensions so that the first dimension of size greater than 1 is first.
Removes any trailing dimensions of size 1.
Operates along the first dimension.
The output is an (N+1)-D array whose first two dimensions have lengths
fland NF.Timetable —
framesigoperates along the rows of the input timetable and returns a timetable whose row times are the row times of the frame centers. The inputxmust be regular and can have either a single variable containing a vector or matrix, or multiple variables each containing a vector.Unformatted
dlarrayobject —framesigoperates exactly as it does on N-D arrays. The output is an unformatteddlarrayobject. You must have a Deep Learning Toolbox™ license to usedlarrayobjects.
Example: cos(2*pi*(0:200)/100).
Example: reshape(1:24,3,4,2).
Example: timetable(randn(20,3),SampleRate=5).
Example: dlarray(randn(3,5)).
Data Types: double | single | timetable | dlarray
Complex Number Support: Yes
Frame length, specified in samples as a positive integer scalar.
fl must be smaller than or equal to the length of input
x.
Example: fl = 5.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: framesig(x,5,Window=hann(35),IncompleteFrameRule="zeropad")
partitions a signal x into frames of length 5 using
the 35-sample Hann window and the zero-pad incomplete frame rule as name-value pair
arguments.
Window, specified as a vector.
The length of Window must be equal to the frame length
fl. When Window is specified,
framesig splits each channel of x into
Window-length frames and then multiplies each frame by the
real-valued floating-point vector Window.
Example: hann(30) and
(1-cos(2*pi*(0:29)'/29))/2 both specify a Hann window of length
30.
Data Types: double | single | dlarray
Overlap length, specified as a nonnegative integer scalar. OverlapLength
is the number of overlap samples between adjoining frames.
OverlapLength must be nonnegative, smaller than the frame
length, and applies only when UnderlapLength is not
specified.
Underlap length, specified as a nonnegative integer scalar.
UnderlapLength is the number of samples to be skipped after
each frame, thus reducing the frame rate. UnderlapLength must be
nonnegative and applies only when OverlapLength is not
specified.
Array of initial conditions that is stacked on top of the input signal, specified
as a vector, matrix, N-D array, timetable, or unformatted
dlarray object.
The array must have such a shape that it can be concatenated with the input signal along the first array dimension of length greater than 1.
If the input signal is a regular timetable, then
InitialConditionmust also be a regular timetable with the same time step and the same variable names as the input timetable. The row times of the initial condition timetable must be such that concatenating it with the input timetable results in a regular timetable.
Example: framesig(3:17,4,InitialCondition=[0 0 0]) partitions a
15-sample vector into frames with a length of four samples. The initial condition is
also a vector.
Example: framesig([1:5;19:23]',3,InitialCondition=[-1 -1; 0 0])
partitions a 5-by-2 matrix into frames with a length of three samples. The initial
condition is also a matrix, which 2-by-2 size enables concatenation with the input
matrix signal.
Data Types: double | single | timetable | dlarray
Complex Number Support: Yes
Initial index, specified as a positive integer scalar. InitialIndex indicates the index of the first element from which the framing operation starts. Equivalently, InitialIndex-1 is the number of initial data samples in x to discard.
Incomplete frame rule, specified as either "drop" or
"zeropad". IncompleteFrameRule specifies the
rule to handle incomplete frames when the input does not have enough remaining samples
to fill up the last frame, if there is one.
"drop"—framesigdrops the incomplete frame."zeropad"—framesigpads the incomplete frame with zeros.
Data Types: char | string
Dimension, specified as a positive integer scalar. Dimension
indicates the dimension along which to frame the input signal x.
If
xis an N-D array,Dimensionmust be a positive integer scalar between1and N.If you do not specify
Dimension, theframesigfunction computes the frames along the first array dimension of size greater than 1.
This argument does not support timetable inputs.
Output Arguments
Framed signal, returned as a matrix.
Final condition output, returned as a vector.
If you specify
IncompleteFrameRuleas"zeropad", thenfnlcondis empty.If you specify
OverlapLength, thenfnlcondcontains the lastOverlapLengthsamples of the last complete frame and any samples that might remain from the incomplete frame, if there is one.If you specify
UnderlapLength, thenfnlcondcontains only the remaining samples in the incomplete frame, if there are any. The final condition array has the same dimensions as the input signal.You can use
fnlcondas the initial condition input for a subsequent framing iteration in a sequence of consecutive framing operations, preserving the desired overlap or underlap from frame to frame.
Final index output, returned as a positive integer scalar.
If you specify
OverlapLengthor setIncompleteFrameRuleto"zeropad", thenfnlidxis1.When you specify
UnderlapLength,fnlidx-1indicates the difference betweenUnderlapLengthand the number of samples inxskipped after the last complete frame. The example Continuous Buffers with Overlap and Underlap Framing illustrates this concept.You can use
fnlidxas the initial index for a subsequent framing iteration in a sequence of consecutive framing operations, preserving the desired underlap from frame to frame.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2024a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)