goertzel
Discrete-Time Fourier transform with second-order Goertzel algorithm
Description
dft = goertzel(data)data using a second-order Goertzel algorithm. If
data has more than one dimension, then goertzel
operates along the first array dimension with size greater than 1. For more information, see
Algorithms.
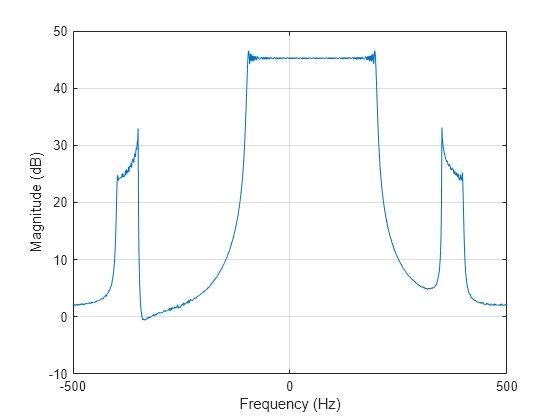
Examples
Input Arguments
Output Arguments
Tips
Use the Goertzel algorithm for best efficiency when you need the DTFT at only a few frequencies.
You can also compute the DTFT with:
Algorithms
The Goertzel algorithm implements the discrete-time Fourier transform X(k) as the convolution of an N-point input x(n), n = 0, 1, …, N – 1, with the impulse response
where u(n), the unit step sequence, is 1 for n ≥ 0 and 0 otherwise. k does not have to be an integer. At a frequency f = kfs/N, where fs is the sample rate, the transform has a value
where
and x(N) = 0. The Z-transform of the impulse response is
with this direct form II implementation:
References
[1] Burrus, C. Sidney, and Thomas W. Parks. DTFT/FFT and Convolution Algorithms: Theory and Implementation. New York: John Wiley & Sons, 1985.
[2] Proakis, John G., and Dimitris G. Manolakis. Digital Signal Processing: Principles, Algorithms, and Applications. 3rd Edition. Upper Saddle River, NJ: Prentice Hall, 1996.
[3] Sysel, Petr, and Pavel Rajmic. “Goertzel Algorithm Generalized to Non-Integer Multiples of Fundamental Frequency.” EURASIP Journal on Advances in Signal Processing. Vol. 2012, Number 1, December 2012, pp. 56-1–56-8. https://doi.org/10.1186/1687-6180-2012-56.
Extended Capabilities
Version History
Introduced before R2006a