SOC Estimator (Adaptive Kalman Filter)
State of charge and terminal resistance estimator with adaptive Kalman filter
Since R2022b
Libraries:
Simscape /
Battery /
BMS /
Estimators
Description
The SOC Estimator (Adaptive Kalman Filter) block implements an estimator that calculates the state of charge (SOC) and terminal resistance of a battery by using the Kalman filter algorithms. The terminal resistance, R0, is a state of the estimator.
The SOC is the ratio of the released capacity Creleasable to the rated capacity Crated. Manufacturers provide the value of the rated capacity of each battery, which represents the maximum amount of charge in the battery:
This block supports single-precision and double-precision floating-point simulation.
Note
To enable inherited single-precision floating-point simulation, the data type of all
inputs and parameters, except for the Sample time (-1 for
inherited) parameter, must be single.
For continuous-time simulation, set the Filter type parameter to
Extended Kalman-Bucy filter or Unscented
Kalman-Bucy filter.
Note
Continuous-time implementation of this block works only in a double-precision floating-point simulation. If you provide single-precision floating-point parameters and inputs, this block casts them to double-precision floating-point values to prevent errors.
For discrete-time simulation, set the Filter type parameter to
Extended Kalman filter or Unscented Kalman
filter and the Sample time (-1 for inherited)
parameter to a positive value or -1.
Equations
These figures show the equivalent circuit for a battery with one-time-constant dynamics and two time-constant dynamics, respectively:
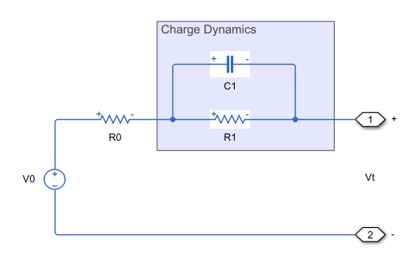
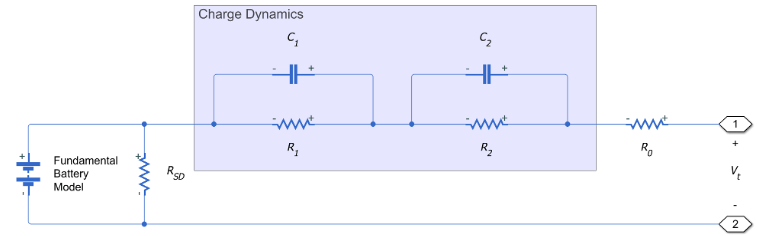
The equations for the equivalent circuit with the terminal resistance R0 as an additional state and two time-constant dynamics are:
where
SOC is the state of charge.
i is the current.
V0 is the no-load voltage.
Vt is the terminal voltage.
AH is the ampere-hour rating.
R1 is the first polarization resistance.
C1 is the first parallel RC capacitance.
R2 is the second polarization resistance.
C2 is the second parallel RC capacitance.
T is the temperature.
V1 is the polarization voltage over the first RC network.
V2 is the polarization voltage over the second RC network.
A time constant τ1 for the first parallel section relates the first polarization resistance R1 and the first parallel RC capacitance C1 using the relationship
A time constant τ2 for the second parallel section relates the second polarization resistance R2 and the second parallel RC capacitance C2 using the relationship
For the Kalman filter algorithms, the block uses this state and these nonlinear process and observation functions:
If you set the Charge dynamics parameter to Two
time-constant dynamics, for the Kalman filter algorithms, the
block uses this state and these process and observation functions:
This diagram shows the structure of the extended Kalman filter (EKF):

The EKF technique relies on a linearization at every time step to approximate the nonlinear system. To linearize the system at every time step, the algorithm computes these Jacobians online:
The EKF is a discrete-time algorithm. After the discretization, the Jacobians for the SOC estimation of the battery are:
where TS is the sample time and VOC is the open-circuit voltage.
The EKF algorithm comprises these phases:
Initialization
— State estimate at time step 0 using measurements at time step 0.
— State estimation error covariance matrix at time step 0 using measurements at time step 0.
Prediction
Project the states ahead (a priori):
Project the error covariance ahead:
where Q is the covariance of the process noise.
Correction
Compute the Kalman gain:
where R is the covariance of the measurement noise.
Update the estimate with the measurement y(k) (a posteriori):
Update the error covariance:
This diagram shows the structure of the extended Kalman-Bucy filter (EKBF):

The EKBF is the continuous-time variant of the Kalman filter. In continuous time, the prediction and correction steps are coupled. The EKBF algorithm comprises these phases:
Initialization
— State estimate at time t0.
— State estimation error covariance matrix at time t0.
Prediction-Correction EKBF algorithm
where:
This diagram shows the structure of the unscented Kalman filter (UKF):

The EKF locally approximates nonlinear functions with the linear equations obtained from the Taylor expansion by using only the first term of the expansion. In a highly nonlinear system, these solutions are not very accurate.
The UKF uses nonlinear transformations on a set of sigma points that the algorithm chooses deterministically. This technique is called unscented transformation. The mean and the covariance matrix of the transformed points are accurate to the second order of the Taylor series expansion.
The UKF algorithm follows these steps:
Initialization
— State estimate at time step 0 using measurements at time step 0.
— State estimation error covariance matrix at time step 0 using measurements at time step 0.
Generate sigma points and calculate the mean weight and covariance weight for each point.
Choose the sigma points, x(i)(k|k)
where:
n is the dimension of the state vector x.
describes the distance between the sigma point and the mean point. In a normal distribution, β = 2 and κ = 0.
is the ith row or column of . The block calculates the matrix square root by using numerically efficient and stable methods such as the Cholesky decomposition.
Perform first estimation of the system state matrix:
Perform first estimation of the covariance matrix of the state variables:
Estimate the measured variables:
Estimate the covariance of the measurement (Py) and covariance between the measurement and the state (Pxy):
Compute the Kalman filter gain:
Perform the second update of the state matrix and of the covariance of the state variables:
This diagram shows the structure of the unscented Kalman-Bucy filter (UKBF):
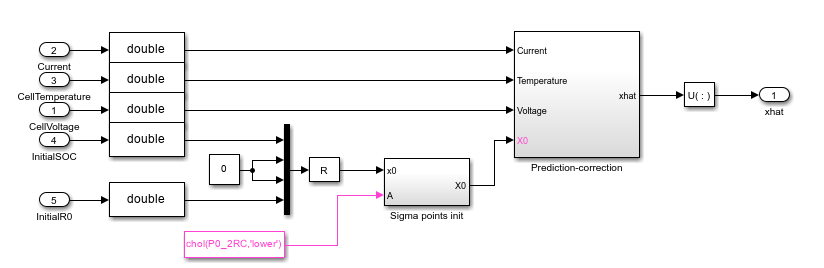
The derived continuous-time filtering equations of the UKBF are similar to the EKBF equations.
Because the UKF uses matrix square roots in its sigma points, the algorithm obtains the square-root version of the UKBF by formulating the filter as a differential equation for the sigma points. The equations for the square-root UKBF are:
where
is the sigma-point matrix.
is a function that returns the lower diagonal part of the argument.
is the ith column of the argument matrix.
Examples
Assumptions and Limitations
Process and sensor noises are independent, zero-mean, Gaussian noises.
Battery nominal capacity does not consider aging.
Ports
Input
Output
Parameters
References
[1] Grewal, Mohinder S., and Angus P. Andrews. Kalman Filtering: Theory and Practice Using MATLAB. 2nd ed. New York: Wiley, 2001.
[2] Van der Merwe, R., and E. A. Wan, The Square-Root Unscented Kalman Filter for State and Parameter-Estimation. 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.01CH37221), vol. 6, IEEE, 2001, pp. 3461–64.
[3] Sarkka, Simo On Unscented Kalman Filtering for State Estimation of Continuous-Time Nonlinear Systems. IEEE Transactions on Automatic Control, vol. 52, no. 9, pp. 1631-1641, Sept. 2007, doi: 10.1109/TAC.2007.904453.
[4] Huria, Tarun, Massimo Ceraolo, Javier Gazzarri, and Robyn Jackey. Simplified Extended Kalman Filter Observer for SOC Estimation of Commercial Power-Oriented LFP Lithium Battery Cells.2013, pp. 2013-01–1544.

