Telescoping Joint
Joint with one spherical and one prismatic joint primitive
Libraries:
Simscape /
Multibody /
Joints
Description
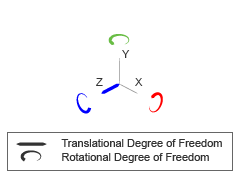
The Telescoping Joint block provides three rotational and one translational degrees of freedom between two frames as shown in the image.
The follower frame can transform with respect to the base frame through a 3-D rotation following by a translation along the z-axis of the follower frame. The figure shows the sequence in which the joint transformations occur at a given simulation time step.

The 3-D rotation does not have kinematic singularity because the rotation is encoded as a quaternion.
To specify the target of the initial state for a joint primitive, use the parameters under State Targets. The targets are specified in the base frame. You can also set the priority levels for the targets. If the joint is not able to satisfy all the state targets, the priority level determines which targets to satisfy first and how closely to satisfy them. For an example, see the Guiding Assembly section of How Multibody Assembly Works.
To model damping and the spring behavior for a joint primitive, use the parameters under Internal Mechanics. Use the Damping Coefficient parameter to model energy dissipation and the Spring Stiffness parameter to model energy storage. Joint springs attempt to displace the joint primitive from its equilibrium position, and joint dampers act as energy dissipation elements. The springs and dampers are strictly linear.
To specify the limits of a joint primitive, use the parameters under Limits. The lower and upper bounds define the width of the free region. The block applies a force to accelerate the joint position back to the free region when the position exceeds the bounds. The block uses a smoothed spring-damper method to compute the force. For more information about the smoothed spring-damper method, see the Description section of the Spatial Contact Force block.
The Force, Torque, and Motion parameters in the Actuation section control the motion of the joint primitives during simulation. For more information, see Specifying Joint Actuation Inputs. Additionally, the joint block has ports that output sensing data, such as position, velocity, acceleration, force, and torque, that you can use to perform analytical tasks on a model. For more information, see Sensing and Force and Torque Sensing.
To specify the joint mode configuration, use the Mode parameter. For more details, see Mode Configuration under the Ports and Parameters sections.
Faults
Using mode faults, you can change the joint modes during a simulation without modifying the
model design. The fault injection overrides the mode setting. For example, if a joint has
the Mode parameter set to Locked and the
Fault behavior parameter set to Disengaged, the
joint becomes disengaged.
To add a mode fault to a joint block, click on the joint block, in the Simscape Block tab, and the Faults section,
click Fault > Add Fault.
Alternatively, you can click the joint block, hover over the ellipsis to open the action
bar, and click the Add a fault on the block icon ![]() . You can add multiple faults to a joint block, but the
joint block can have only one active fault during a simulation.
. You can add multiple faults to a joint block, but the
joint block can have only one active fault during a simulation.
As you add faults, in the Property Inspector, under the Fault
section, specify the behavior and the trigger type of the fault. To define the fault
behavior, click the link next to the Fault Behavior. This
joint supports Locked, Normal, or
Disengaged mode. The joint blocks support these trigger types:
Always on, Timed, Manual, and
Conditional. For more details of these trigger types, see Set Fault Triggers. To trigger a
conditional fault, you can use Simulink signals, Simscape language blocks, and MATLAB
workspace variables. To set the active fault for a block, use the Fault Table. For more
details, see Access the Fault Table and Fault Dashboard.
To enable fault simulation, in the Simscape Block tab and
the Faults section, turn on the Fault
Simulation button. The fault simulation is on when the button is green and
the status is on. The simulation logs the trigger status
data. To view the data, use the Simulation Data
Inspector. Also, you can see the fault status and a summary of the triggered
faults in the Fault Dashboard. To open the Fault Dashboard, in the Simscape Block tab, click Faults >
Fault Dashboard.
To create and modify faults, you can also use Simscape™ and Simulink® fault functions. For more details, see the function section of the Simulink Fault Controls and Simscape Faults Interface.
Ports
Frame
Base frame of the joint block.
Follower frame of the joint block.
Input
Spherical Primitive (S)
Physical signal input port that accepts the actuation torque for the spherical primitive. The signal has a scalar format that represents the torque about the x-axis of the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Actuation, set Torque to Provided by Input and select Torque (X).
Physical signal input port that accepts the actuation torque for the spherical primitive. The signal has a scalar format that represents the torque about the y-axis of the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Actuation, set Torque to Provided by Input and select Torque (Y).
Physical signal input port that accepts the actuation torque for the spherical primitive. The signal has a scalar format that represents the torque about the z-axis of the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Actuation, set Torque to Provided by Input and select Torque (Z).
Physical signal input port that accepts the actuation torque for the spherical primitive. The vector represents the actuation torque to apply between the base and follower frame as expressed in resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Actuation, set Motion to Provided by Input and select Torque (XYZ).
Z Prismatic Primitive (Pz)
Physical signal input port that accepts the actuation force for the joint primitive. The block applies this force equally and oppositely to the base and follower frames of the joint along the z-axis of the base frame.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Actuation, set Force to Provided by
Input.
Physical signal input port that accepts the motion profile for the joint primitive. The block uses this signal to determine the displacement of the follower frame with respect to the base frame along the z-axis of the base frame. The signal must also contain the first and second derivatives of the displacement.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Actuation, set Motion to Provided by
Input.
Mode Configuration
Input port that controls the mode of the joint. The signal must be a unitless scalar. The
joint mode is normal when the input signal is 0, disengaged when
the input signal is -1, and locked when the input signal is
1. You can change the mode at any time during the
simulation.
The table shows how the position and velocity of the joint change during transitions between modes.
| Transitions | Position | Velocity |
|---|---|---|
| Normal to Locked | The joint position retains the current value and remains constant after the transition. | The joint velocity becomes zero and remains constant after the transition. |
| Normal to Disengaged | The joint position retains the current value but can change in any direction after the transition. | The joint velocity retains the current value but can change in any direction after the transition. |
| Locked to Normal | The joint position retains the current value but can change in the directions aligned with the joint degrees of freedom (DOFs) after the transition. | The joint velocity remains at zero but can change in the directions aligned with the joint DOFs after the transition. |
| Locked to Disengaged | The joint position retains the current value but can change in any direction after the transition. | The joint velocity remains at zero but can change in any direction after the transition. |
| Disengaged to Normal | For the directions aligned with the joint DOFs, the joint positions initially take values calculated by using Newton's method and can change thereafter. In the constrained directions, the joint positions become zero and remain constant after the transition. | For the directions aligned with the joint DOFs, the joint velocities initially take values calculated by using Newton's method and can change thereafter. In the constrained directions, the joint velocities become zero and remain constant after the transition. |
| Disengaged to Locked | For the directions aligned with the joint DOFs, the joint positions initially take values calculated by using Newton's method and remain constant after the transition. In the constrained directions, the joint positions become zero and remain constant after the transition. | The joint velocity becomes zero and remains constant after the transition. |
Dependencies
To enable this port, under Mode Configuration, set Mode to Provided by Input.
Output
Spherical Primitive (S)
Orientation of the follower frame with respect to the base frame, returned as a unit quaternion. See Quaternion Measurements for more information.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Position.
x-coordinate of the relative angular velocity, returned as a scalar. The value is resolved in the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Velocity (X).
y-coordinate of the relative angular velocity, returned as a scalar. The value is resolved in the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Velocity (Y).
z-coordinate of the relative angular velocity, returned as a scalar. The value is resolved in the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Velocity (Z).
Relative angular velocity, returned as a 3-D vector resolved in the resolution frame.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Velocity.
x-coordinate of the relative angular acceleration, returned as a scalar. This quantity equals the time derivative of the signal exported from the port wx.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Acceleration (X).
y-coordinate of the relative angular acceleration, returned as a scalar. This quantity equals the time derivative of the signal exported from the port wy.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Acceleration (Y).
z-coordinate of the relative angular acceleration, returned as a scalar. This quantity equals the time derivative of the signal exported from the port wz.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Acceleration (Z).
Relative angular acceleration, returned as a 3-D vector resolved in the resolution frame. This quantity equals the time derivative of the signal exported from the port w.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Acceleration.
Physical signal port that outputs the magnitude of the lower-limit torque. The block applies the lower-limit torque when the angle between the z-axes of the two frames is less than the bound of the lower limit. The torque applies to both the base and follower frames of the spherical primitive to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Signed Lower-Limit Torque Magnitude.
Physical signal port that outputs the magnitude of the upper-limit torque. The block applies the upper-limit torque when the angle between the z-axes of the two frames exceeds the upper bound. The torque applies to both the base and follower frames of the spherical primitive to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Spherical Primitive (S) > Sensing, select Upper-Limit Torque.
Z Prismatic Primitive (Pz)
Physical signal port that outputs the position of the joint primitive. The value is the displacement of the follower frame with respect to the base frame in the z-axis of the base frame.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Position.
Physical signal port that outputs the velocity of the joint primitive. The value is the first derivative of the signal from the port pz.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Velocity.
Physical signal port that outputs the acceleration of the joint primitive. The value is the second derivative of the signal from the port pz.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Acceleration.
Physical signal port that outputs the actuator force acting on the joint primitive.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Actuator Force.
Physical signal port that outputs the lower-limit force. The block applies this force when the joint primitive position is less than the lower bound of the free region. The block applies this force to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Lower-Limit Force.
Physical signal port that outputs the upper-limit force. The block applies this force when the joint primitive position exceeds the upper bound of the free region. The block applies this force to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Z Prismatic Primitive (Pz) > Sensing, select Upper-Limit Force.
Composite Force/Torque Sensing
Physical signal port that outputs the constraint forces that act across the joint.
These forces maintain the translational constraints of the joint. The output has a
3-by-1 vector format and represents the force components along the
x, y, and z axes of the
resolution frame. For more information, see Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Constraint Force.
Physical signal port that outputs the constraint torques that act across the
joint. These torques maintain the rotational constraints of the joint. The output
has a 3-by-1 vector format and represents the torque components about the
x, y, and z axes of the
resolution frame. For more information, see Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Constraint Torque.
Physical signal port that outputs the total force that acts across the joint. The
total force is the sum of the of all forces transmitted between the connected frames
through the joint. The output has a 3-by-1 vector format and represents the force
components along the x, y, and
z axes of the resolution frame.
To demonstrate the total force acting on a joint, the figure shows a model using a Prismatic Joint block.

The total force includes the actuator force (FA), internal force (FI), and constraint forces (FC). For more information, see Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Total Force.
Physical signal port that outputs the total torque that acts across the joint. The
total torque is the sum of all torques transmitted between the connected frames
through the joint. The torque includes the actuation, internal, limit, and
constraint torques. The output has a 3-by-1 vector format and represents the torque
components about the x, y, and
z axes of the resolution frame. For more information, see
Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Total Torque.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Spherical Primitive (S)
State Targets
Select this parameter to specify the target of the relative orientation between the base and follower frames.
Priority level of the relative orientation target, specified as High (desired) or Low (approximate). See Guiding Assembly for more information.
Dependencies
To enable this parameter, select Specify Position Target.
Method to use to specify the relative orientation target between the base and follower frames.
When you set the parameter to None, the orientation
target has the base and follower frames aligned.
Dependencies
To enable this parameter, select Specify Position Target.
Follower frame axis used to align with the base frame axis set by the Pair 1: Base parameter, specified as an orthogonal axis of the follower frame. The follower frame rotates with respect to the base frame to enable the alignment between the selected axes of the base and follower frames.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Aligned Axis.
Base frame axis to align with the follower frame specified by the Pair 1: Follower, specified as an orthogonal axis of the base frame.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Aligned Axis.
Base frame axis to align with the follower frame specified by the Pair 2: Follower, specified as an orthogonal axis of the follower frame. The follower frame rotates with respect to the base frame to enable the alignment between the selected axes of the base and follower frames.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Aligned Axis.
Base frame axis used to let the follower frame axis set in the Pair2: Follower parameter to align with, specified as an orthogonal axis of the base frame. The axis choices for Pair 2 depend on the Pair 1 axis selections.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Aligned Axis.
Axis of the relative rotation, specified as an orthogonal axis of the base frame.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Standard Axis.
Angle of the relative rotation, specified as a scalar. The angle indicates the rotation of the follower frame with respect to the base frame about the specified axis.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Standard Axis.
Axis of the relative rotation, specified as a 3-by-1 unit vector. The vector is dimensionless and indicates the rotational axis resolved in the base frame.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Arbitrary Axis.
Angle of the relative rotation, specified as a scalar. The angle indicates the rotation of the follower frame with respect to the base frame about the axis specified by the Axis parameter.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Arbitrary Axis.
Frame whose axes to rotate the follower frame about, specified as Follower Axes or Base Axes. If you set the parameter to Follower Axes, the follower frame rotates about its own axes, and the follower frame changes the orientation with each successive rotation. If you set the parameter to Base Axes, the follower frame rotates about the fixed base frame axes. See Rotational Measurements for more information.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Rotation Sequence.
Sequence of the rotation axis for three successive elementary rotations. See Rotation Sequence Measurements for more information.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Rotation Sequence.
Angles for the rotation sequence parameterization, specified as a 1-by-3 vector. See Rotation Sequence Measurements for more information.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to
Rotation Sequence.
Relative rotation, specified as a 3-by-3 matrix that maps vectors from the follower frame to the base frame. The matrix must be orthogonal and have determinant 1. See Rotational Measurements for more information.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Rotation Matrix.
Relative rotation, specified as a unit quaternion vector. See Rotational Measurements for more information about the quaternion.
Dependencies
To enable this parameter, under Specify Position Target > Value, set Method parameter to Quaternion.
Select this parameter to specify the angular velocity target for the spherical primitive.
Priority level of the angular velocity target, specified as High
(desired) or Low (approximate). See
Guiding Assembly for more information.
Dependencies
To enable this parameter, select Specify Velocity Target.
Angular velocity target for the spherical primitive, specified as a 1-by-3 vector resolved in resolution frame.
Dependencies
To enable this parameter, select Specify Velocity Target.
Frame used to resolve the specified angular velocity target, specified as one of these:
Base— The joint block resolves the angular velocity target in the coordinates of the base frame.Follower— The joint block resolves the angular velocity target in the coordinates of the follower frame.
Internal Mechanics
Method to use to specify the orientation of the equilibrium frame with respect to the base
frame. The equilibrium frame remains fixed relative to the base frame throughout
the simulation. When you set the parameter to None,
the equilibrium frame aligns with the base frame.
When the follower and equilibrium frames are aligned, the spring torque of the spherical primitive is zero.
Equilibrium frame axis used to align with the base frame axis set by the Pair 1: Base parameter, specified as an orthogonal axis of the equilibrium frame. The equilibrium frame rotates with respect to the base frame to enable the alignment between the selected axes of the base and equilibrium frames.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Aligned Axis.
Base frame axis to align with the equilibrium frame specified by the Pair 1: Follower, specified as an orthogonal axis of the base frame.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Aligned Axis.
Base frame axis to align with the equilibrium frame specified by the Pair 2: Follower, specified as an orthogonal axis of the equilibrium frame. The equilibrium frame rotates with respect to the base frame to enable the alignment between the selected axes of the base and equilibrium frames.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Aligned Axis.
Base frame axis used to let the equilibrium frame axis set in the Pair2: Follower parameter to align with, specified as an orthogonal axis of the base frame. The axis choices for Pair 2 depend on the Pair 1 axis selections.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Aligned Axis.
Axis of the relative rotation, specified as an orthogonal axis of the base frame.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Standard Axis.
Angle of the relative rotation, specified as a scalar. The angle indicates the rotation of the equilibrium frame with respect to the base frame about the specified axis.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Standard Axis.
Axis of the relative rotation, specified as a 3-by-1 unit vector. The vector is dimensionless and indicates the rotational axis resolved in the base frame.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Arbitrary Axis.
Angle of the relative rotation, specified as a scalar. The angle indicates the rotation of the equilibrium frame with respect to the base frame about the axis specified by the Axis parameter.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Arbitrary Axis.
Frame whose axes to rotate the equilibrium frame about, specified as Follower Axes or Base Axes. If you set the parameter to Follower Axes, the equilibrium frame rotates about its own axes, and the equilibrium frame changes the orientation with each successive rotation. If you set the parameter to Base Axes, the equilibrium frame rotates about the fixed base frame axes. See Rotational Measurements for more information.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Rotation Sequence.
Sequence of the rotation axis for three successive elementary rotations. See Rotation Sequence Measurements for more information.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Rotation Sequence.
Angles for elementary rotations, specified as a 1-by-3 vector. See Rotation Sequence Measurements for more information.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Rotation Sequence.
Relative rotation, specified as a 3-by-3 matrix. The matrix must be orthogonal and have determinant 1. See Rotational Measurements for more information.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Rotation Matrix.
Relative rotation, specified as a unit quaternion vector. See Rotational Measurements for more information about the quaternion.
Dependencies
To enable this parameter, under Equilibrium Position, set Method parameter to Quaternion.
Stiffness of the internal spring-damper force law for the spherical primitive, specified as a scalar with a unit of rotational stiffness.
The spring attempts to pull the follower frame so that the follower frame is aligned with the specified equilibrium frame.
Damping coefficient of the internal spring-damper force law for the spherical primitive, specified as a scalar with a unit of rotational damping coefficient.
Limits
Select this parameter to specify the lower limit of the spherical primitive. Joint limits use spring-dampers to resist travel past the bounds of the range.
Lower bound for the free region of the spherical primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Lower Limit.
Stiffness of the spring at lower bound, specified as a scalar with a unit of rotational stiffness.
Dependencies
To enable this parameter, select Specify Lower Limit.
Damping coefficient at lower bound, specified as a scalar with a unit of rotational damping coefficient.
Dependencies
To enable this parameter, select Specify Lower Limit.
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the lower-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of torques and the smaller the time-step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy while expanding it improves speed.
Dependencies
To enable this parameter, select Specify Lower Limit.
Select this parameter to specify the upper limit of the spherical primitive. Joint limits use spring-dampers to resist travel past the bounds of the range.
Upper bound for the free region of the spherical primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Upper Limit.
Stiffness of the spring at upper bound, specified as a scalar with a unit of stiffness.
Dependencies
To enable this parameter, select Specify Upper Limit.
Damping coefficient at upper bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Upper Limit.
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the upper-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of torques and the smaller the time-step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy while expanding it improves speed.
Dependencies
To enable this parameter, select Specify Upper Limit.
Actuation
Option to provide the actuation torque for the spherical primitive, specified as one of these values.
| Actuation Torque Setting | Description |
|---|---|
None | Apply no actuation torque. |
Provided by Input | Apply actuation torques based on physical signals. The signal specifies the torque acting on the follower frame with respect to the base frame. The signal provides the value of the torque applied equally and oppositely to the base and follower frames. Selecting this option exposes additional parameters that you can use to enable input ports See the Input section for details. |
Frame used to resolve the input actuation torques, specified as Base or Follower.
Sensing
Frame used to resolve the sensing output signals, specified as
Base or Follower. For
more information about the output signals, see the Output
section.
Z Prismatic Primitive (Pz)
State Targets
Select this parameter to specify the position target for the z prismatic primitive.
Priority level of the position target, specified as High (desired)
or Low (approximate).
For more information, see the Guiding Assembly
section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Position Target.
Position target of the z prismatic primitive, specified as a scalar in units of length.
Dependencies
To enable this parameter, select Specify Position Target.
Select this parameter to specify the linear velocity target for the z prismatic primitive.
Priority level of the linear velocity target, specified as High
(desired) or Low
(approximate). For more information,
see the Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Velocity Target.
Linear velocity target for the z prismatic primitive, specified as a scalar in units of linear velocity.
Dependencies
To enable this parameter, select Specify Velocity Target.
Internal Mechanics
Position where the spring force is zero, specified as a scalar in units of length.
Stiffness of the internal spring-damper force law for the joint primitive, specified as a scalar in units of linear stiffness.
Damping coefficient of the internal spring-damper force law for the joint primitive, specified as a scalar in units of linear damping coefficient.
Limits
Select this parameter to specify the lower limit of the z prismatic primitive.
Lower bound of the free region of the z prismatic primitive, specified as a scalar in units of length.
Dependencies
To enable this parameter, select Specify Lower Limit.
Stiffness of the spring at the lower bound, specified as a scalar in units of linear stiffness.
Dependencies
To enable this parameter, select Specify Lower Limit.
Damping coefficient at the lower bound, specified as a scalar in units of linear damping coefficient.
Dependencies
To enable this parameter, select Specify Lower Limit.
Region to smooth the spring and damper forces, specified as a scalar in units of length.
The block applies the full value of the lower-limit force when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Lower Limit.
Select this parameter to specify the upper limit of the z prismatic primitive.
Upper bound for the free region of the joint primitive, specified as a scalar in units of length.
Dependencies
To enable this parameter, select Specify Upper Limit.
Stiffness of the spring at the upper bound, specified as a scalar in units of linear stiffness.
Dependencies
To enable this parameter, select Specify Upper Limit.
Damping coefficient at the upper bound, specified as a scalar in units of linear damping coefficient.
Dependencies
To enable this parameter, select Specify Upper Limit.
Region to smooth the spring and damper forces, specified as a scalar in units of length.
The block applies the full value of the upper-limit force when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Upper Limit.
Actuation
Option to provide the actuator force for the joint primitive, specified as one of these values:
| Force Setting | Description |
|---|---|
None | No actuator force. |
Provided by Input | The input port fz specifies the actuator force for the z prismatic primitive. |
Automatically Computed | The block automatically calculates the amount of force required to satisfy the motion inputs
to the mechanism. If you set this parameter to
Automatically Computed,
you do not need to set Motion
to Provided by Input
for the same joint primitive. The automatically
computed force may satisfy a motion input
elsewhere in the mechanism. |
Option to provide the motion for the joint primitive, specified as one of these values:
| Motion Setting | Description |
|---|---|
Automatically Computed | The block computes and applies the joint primitive motion based on the model dynamics. |
Provided by Input | The input port pz specifies the motion for the joint primitive. |
Mode Configuration
Joint mode for the simulation, specified as one of these values:
| Mode | Description |
|---|---|
Locked | Locked mode constrains all the degrees of freedom (DOFs) for the joint. The locked joint maintains its initial assembly position with zero velocity during the simulation. The joint block can sense forces or torques in accordance with the settings of the Internal Mechanics, Limits, and Actuation parameters. |
Normal | Normal mode enables the DOFs and the constraints of the joint work as intended during the simulation. |
Disengaged | Disengaged mode releases the joint from all constraints throughout the simulation. The settings for Internal Mechanics, Limits, and Actuation parameters do not affect the disengaged joint. All output ports output zero. |
Provided by Input | The Provided by Input option allows you to specify the joint mode
by using an input signal. For more information, see the port
mode in the Input
section. |
Composite Force/Torque Sensing
Measurement direction, specified as one of these values:
Follower on Base— The block senses the force and torque that the follower frame exerts on the base frame.Base on Follower— The block senses the force and torque that the base frame exerts on the follower frame.
This parameter affects only the output signals under the Composite Force/Torque Sensing section. Reversing the direction changes the sign of the measurements. For more information, see Force and Torque Measurement Direction.
Frame used to resolve the measurements, specified as one of these values:
Base— The block resolves the measurements in the coordinates of the base frame.Follower— The block resolves the measurements in the coordinates of the follower frame.
This parameter affects only the output signals under the Composite Force/Torque Sensing section.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2012aYou can now model mode faults for all the joint blocks. Using the faults, you can change the joint modes during a simulation without changing the model design. For more information, see the Faults section in the description.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
