Synchronous Machine Round Rotor
Round-rotor synchronous machine with fundamental or standard parameterization
Libraries:
Simscape /
Electrical /
Electromechanical /
Synchronous
Description
The Synchronous Machine Round Rotor block models a round-rotor synchronous machine using fundamental or standard parameters.
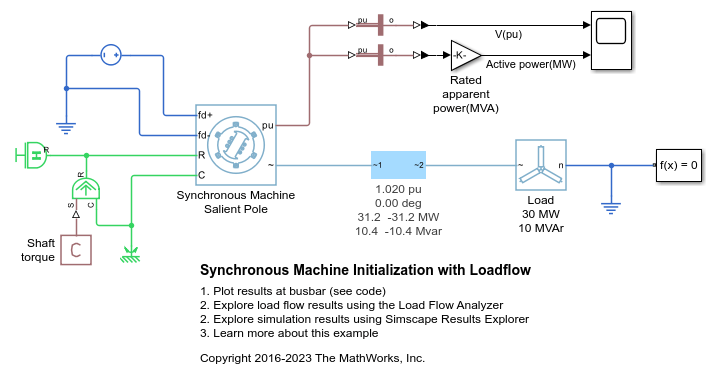
Synchronous Machine Initialization Using Load-Flow Target Values
If the block is in a network that is compatible with the frequency-time simulation mode, you can perform a load-flow analysis on the network. A load-flow analysis provides steady-state values that you can use to initialize the machine.
For more information, see Perform a Load-Flow Analysis Using Simscape Electrical and Frequency and Time Simulation Mode. For an example that shows how to initialize a synchronous machine using data from a load-flow analysis, see Synchronous Machine Initialization with Loadflow.
Equations
The synchronous machine equations are expressed with respect to a rotating reference frame, defined by
where:
θe is the electrical angle.
N is the number of pole pairs.
θr is the rotor angle.
The Park transformation maps the synchronous machine equations to the rotating reference frame with respect to the electrical angle. The Park transformation is defined by
The Park transformation is used to define the per-unit synchronous machine equations. The stator voltage equations are defined by
and
where:
ed, eq, and e0 are the d-axis, q-axis, and zero-sequence stator voltages, defined by
va, vb, and vc are the stator voltages measured from port ~ to neutral port n.
ωbase is the per-unit base electrical speed.
ψd, ψq, and ψ0 are the d-axis, q-axis, and zero-sequence stator flux linkages.
ωr is the per-unit rotor rotational speed.
Ra is the stator resistance.
id, iq, and i0 are the d-axis, q-axis, and zero-sequence stator currents, defined by
ia, ib, and ic are the stator currents flowing from port ~ to port n.
The rotor voltage equations are defined by
and
where:
efd is the field voltage.
e1d, e1q, and e2q are the voltages across the d-axis damper winding 1, q-axis damper winding 1, and q-axis damper winding 2. They are all equal to 0.
ψfd, ψ1d, ψ1q, and ψ2q are the magnetic fluxes linking the field circuit, d-axis damper winding 1, q-axis damper winding 1, and q-axis damper winding 2.
Rfd, R1d, R1q, and R2q are the resistances of rotor field circuit, d-axis damper winding 1, q-axis damper winding 1, and q-axis damper winding 2.
ifd, i1d, i1q, and i2q are the currents flowing in the field circuit, d-axis damper winding 1, q-axis damper winding 1, and q-axis damper winding 2.
The saturation equations are defined by
(If saturation is disabled),
(If saturation is enabled),
and
where:
ψad is the d-axis air-gap or mutual flux linkage.
ψaq is the q-axis air-gap or mutual flux linkage.
ψat is the air-gap flux linkage.
Ks is the saturation factor.
Ladu is the unsaturated mutual inductance of the stator d-axis.
Lad is the mutual inductance of the stator d-axis.
Laqu is the unsaturated mutual inductance of the stator q-axis.
Laq is the mutual inductance of the stator q-axis.
The saturation factor function, f, is calculated from the per-unit open-circuit lookup table as:
and
where Vag is the per-unit air-gap voltage.
In per-unit,
and
can be rearranged to
The stator flux linkage equations are defined by
and
where:
Ll is the stator leakage inductance.
Lad and Laq are the mutual inductances of the stator d-axis and q-axis.
The rotor flux linkage equations are defined by
and
where:
Lffd is the self-inductances of the rotor field circuit.
Lffd is the self-inductance of the rotor field circuit.
L11d is the self-inductance of the d-axis damper winding 1.
L11q is the self-inductance of the q-axis damper winding 1.
L22q is the self-inductance of the q-axis damper winding 2.
Lf1d is the rotor field circuit and d-axis damper winding 1 mutual inductance.
The inductances are defined by these equations:
The inductance equations assume that per-unit mutual inductance L12q = Laq, that is, the stator and rotor currents in the q-axis all link a single mutual flux represented by Laq.
The rotor torque is defined by
Plotting and Display Options
You can perform plotting and display actions using the Electrical menu on the block context menu.
Right-click the block and, from the Electrical menu, select an option:
Display Base Values — Displays the machine per-unit base values in the MATLAB® Command Window.
Display Associated Base Values — Displays associated per-unit base values in the MATLAB Command Window.
Display Associated Initial Conditions — Displays associated initial conditions in the MATLAB Command Window.
Plot Open-Circuit Saturation (pu) — Plots air-gap voltage, Vag, versus field current, ifd, both measured in per-unit, in a MATLAB figure window. The plot contains three traces:
Unsaturated — Stator d-axis mutual inductance (unsaturated), Ladu you specify
Saturated — Per-unit open-circuit lookup table (Vag versus ifd) you specify
Derived — Open-circuit lookup table (per-unit) derived from the Per-unit open-circuit lookup table (Vag versus ifd) you specify. This data is used to calculate the saturation factor, Ks, versus magnetic flux linkage, ψat, characteristic.
Plot Saturation Factor (pu) — Plots saturation factor, Ks, versus magnetic flux linkage, ψat, both measured in per-unit, in a MATLAB figure window using the machine parameters. This parameter is derived from other parameters that you specify:
Stator d-axis mutual inductance (unsaturated), Ladu
Per-unit field current saturation data, ifd
Per-unit air-gap voltage saturation data, Vag
Plot Power Capability Curves — Plots active power P versus reactive power Q, both measured in per-unit, in a MATLAB figure window. The plot might contain multiple traces. Each trace corresponds to a maximum field circuit voltage measured in per-unit (non-reciprocal per-unit system). The plot shows the maximum reactive power that the generator produces when operating with a lagging power factor and the minimum reactive power that the generator absorbs when operating with a leading power factor. (since R2023b)
Model Thermal Effects
You can expose thermal ports to model the effects of generated heat and machine temperature. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block does not contain thermal ports.Show thermal port— The block contains multiple thermal conserving ports.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
For this block, the Initial Targets settings are visible only if, in
the Initial Conditions section, you set the Initialization
option parameter to Set targets for rotor angle and Park's
transform variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Ports
Output
Conserving
Parameters
References
[1] Kundur, P. Power System Stability and Control. New York, NY: McGraw Hill, 1993.
[2] Lyshevski, S. E. Electromechanical Systems, Electric Machines and Applied Mechatronics. Boca Raton, FL: CRC Press, 1999.