predictError

Predict error value at a set of points

Syntax

error = predictError(results,XTable)

[error,sigma] = predictError(results,XTable)

Description

error = predictError(results,XTable) returns the posterior mean of the error coupled constraint at the points in XTable.

[error,sigma] = predictError(results,XTable) also returns the posterior standard deviations.

Examples

Error Prediction

This example shows optimizing a function that throws an error when the evaluation point has norm larger than 2. The error model for the objective function learns this behavior.

Create variables named x1 and x2 that range from -5 to 5.

var1 = optimizableVariable('x1',[-5,5]);
var2 = optimizableVariable('x2',[-5,5]);
vars = [var1,var2];

The following objective function throws an error when the norm of x = [x1,x2] exceeds 2:

function f = makeanerror(x)
f = x.x1 - x.x2 - sqrt(4-x.x1^2-x.x2^2);

fun = @makeanerror;

Plot the error model and minimum objective as the optimization proceeds. Optimize for 60 iterations so the error model becomes well-trained. For reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function.

rng default
results = bayesopt(fun,vars,'Verbose',0,'MaxObjectiveEvaluations',60,...
    'AcquisitionFunctionName','expected-improvement-plus',...
    'PlotFcn',{@plotMinObjective,@plotConstraintModels});

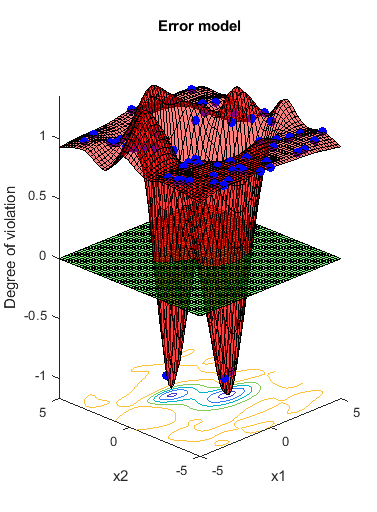
Predict the error at points on the line x1 = x2. If the error model were perfect, it would have value -1 at every point where the norm of x is no more than 2, and value 1 at all other points.

x1 = (-5:0.5:5)';
x2 = x1;
XTable = table(x1,x2);
error = predictError(results,XTable);
normx = sqrt(x1.^2 + x2.^2);
[XTable,table(normx,error)]

ans =

  21x4 table

     x1      x2      normx       error  
    ____    ____    _______    _________

      -5      -5     7.0711      0.94663
    -4.5    -4.5      6.364      0.97396
      -4      -4     5.6569      0.99125
    -3.5    -3.5     4.9497       1.0033
      -3      -3     4.2426       1.0018
    -2.5    -2.5     3.5355      0.99627
      -2      -2     2.8284       1.0043
    -1.5    -1.5     2.1213      0.89886
      -1      -1     1.4142       0.4746
    -0.5    -0.5    0.70711    0.0042389
       0       0          0     -0.16004
     0.5     0.5    0.70711    -0.012397
       1       1     1.4142      0.30187
     1.5     1.5     2.1213      0.88588
       2       2     2.8284       1.0872
     2.5     2.5     3.5355        0.997
       3       3     4.2426      0.99861
     3.5     3.5     4.9497      0.98894
       4       4     5.6569      0.98941
     4.5     4.5      6.364      0.98956
       5       5     7.0711      0.95549

Input Arguments

results — Bayesian optimization results

BayesianOptimization object

Bayesian optimization results, specified as a BayesianOptimization object.

XTable — Prediction points

table with D columns

Prediction points, specified as a table with D columns, where D is the number of variables in the problem. The function performs its predictions on these points.

Data Types: table

Output Arguments

error — Mean of error coupled constraint

N-by-1 vector

Mean of error coupled constraint, returned as an N-by-1 vector, where N is the number of rows of XTable. The mean is the posterior mean of the error coupled constraint at the points in XTable.

bayesopt deems your objective function to return an error if it returns anything other than a finite real scalar. See Objective Function Errors.

sigma — Standard deviation of error coupled constraint

N-by-1 vector

Standard deviation of error coupled constraint, returned as an N-by-1 vector, where N is the number of rows of XTable.

Version History

Introduced in R2016b