predictorImportance

Estimates of predictor importance for classification tree

Syntax

imp = predictorImportance(tree)

Description

imp = predictorImportance(tree) computes estimates of predictor importance for tree by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. imp is returned as a row vector with the same number of elements as tree.PredictorNames. The entries of imp are estimates of the predictor importance, with 0 representing the smallest possible importance.

Examples

Estimate Predictor Importance Values

Load Fisher's iris data set.

load fisheriris

Grow a classification tree.

Mdl = fitctree(meas,species);

Compute predictor importance estimates for all predictor variables.

imp = predictorImportance(Mdl)

imp = 1×4

         0         0    0.0907    0.0682

The first two elements of imp are zero. Therefore, the first two predictors do not enter into Mdl calculations for classifying irises.

Estimates of predictor importance do not depend on the order of predictors if you use surrogate splits, but do depend on the order if you do not use surrogate splits.

Permute the order of the data columns in the previous example, grow another classification tree, and then compute predictor importance estimates.

measPerm  = meas(:,[4 1 3 2]);
MdlPerm = fitctree(measPerm,species);
impPerm = predictorImportance(MdlPerm)

impPerm = 1×4

    0.1515         0    0.0074         0

The estimates of predictor importance are not a permutation of imp.

Surrogate Splits and Predictor Importance

Load Fisher's iris data set.

load fisheriris

Grow a classification tree. Specify usage of surrogate splits.

Mdl = fitctree(meas,species,'Surrogate','on');

Compute predictor importance estimates for all predictor variables.

imp = predictorImportance(Mdl)

imp = 1×4

    0.0791    0.0374    0.1530    0.1529

All predictors have some importance. The first two predictors are less important than the final two.

Permute the order of the data columns in the previous example, grow another classification tree specifying usage of surrogate splits, and then compute predictor importance estimates.

measPerm  = meas(:,[4 1 3 2]);
MdlPerm = fitctree(measPerm,species,'Surrogate','on');
impPerm = predictorImportance(MdlPerm)

impPerm = 1×4

    0.1529    0.0791    0.1530    0.0374

The estimates of predictor importance are a permutation of imp.

Unbiased Predictor Importance Estimates

Load the census1994 data set. Consider a model that predicts a person's salary category given their age, working class, education level, martial status, race, sex, capital gain and loss, and number of working hours per week.

load census1994
X = adultdata(:,{'age','workClass','education_num','marital_status','race',...
    'sex','capital_gain','capital_loss','hours_per_week','salary'});

Display the number of categories represented in the categorical variables using summary.

summary(X)

X: 32561×10 table

Variables:

    age: double
    workClass: categorical (8 categories)
    education_num: double
    marital_status: categorical (7 categories)
    race: categorical (5 categories)
    sex: categorical (2 categories)
    capital_gain: double
    capital_loss: double
    hours_per_week: double
    salary: categorical (2 categories)

Statistics for applicable variables:

                      NumMissing     Min      Median       Max            Mean              Std      

    age                     0         17        37           90           38.5816           13.6404  
    workClass            1836                                                                        
    education_num           0          1        10           16           10.0807            2.5727  
    marital_status          0                                                                        
    race                    0                                                                        
    sex                     0                                                                        
    capital_gain            0          0         0        99999        1.0776e+03        7.3853e+03  
    capital_loss            0          0         0         4356           87.3038          402.9602  
    hours_per_week          0          1        40           99           40.4375           12.3474  
    salary                  0                                                                        

Because there are few categories represented in the categorical variables compared to levels in the continuous variables, the standard CART, predictor-splitting algorithm prefers splitting a continuous predictor over the categorical variables.

Train a classification tree using the entire data set. To grow unbiased trees, specify usage of the curvature test for splitting predictors. Because there are missing observations in the data, specify usage of surrogate splits.

Mdl = fitctree(X,'salary','PredictorSelection','curvature',...
    'Surrogate','on');

Estimate predictor importance values by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. Compare the estimates using a bar graph.

imp = predictorImportance(Mdl);

figure;
bar(imp);
title('Predictor Importance Estimates');
ylabel('Estimates');
xlabel('Predictors');
h = gca;
h.XTickLabel = Mdl.PredictorNames;
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';

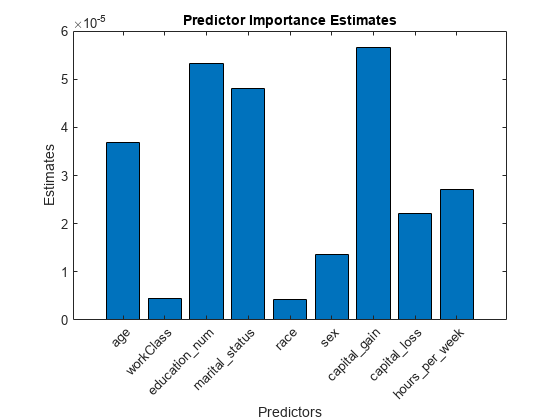
In this case, capital_gain is the most important predictor, followed by education_num.

Input Arguments

tree — Trained classification tree

ClassificationTree model object | CompactClassificationTree model object

Trained classification tree, specified as a ClassificationTree model object trained with fitctree, or a CompactClassificationTree model object created with compact.

More About

Predictor Importance

predictorImportance computes importance measures of the predictors in a tree by summing changes in the node risk due to splits on every predictor, and then dividing the sum by the total number of branch nodes. The change in the node risk is the difference between the risk for the parent node and the total risk for the two children. For example, if a tree splits a parent node (for example, node 1) into two child nodes (for example, nodes 2 and 3), then predictorImportance increases the importance of the split predictor by

(R₁ – R₂ – R₃)/N_branch,

where R_i is the node risk of node i, and N_branch is the total number of branch nodes. A node risk is defined as a node error or node impurity weighted by the node probability:

R_i = P_iE_i,

where P_i is the node probability of node i, and E_i is either the node error (for a tree grown by minimizing the twoing criterion) or node impurity (for a tree grown by minimizing an impurity criterion, such as the Gini index or deviance) of node i.

The estimates of predictor importance depend on whether you use surrogate splits for training.

• If you use surrogate splits, predictorImportance sums the changes in the node risk over all splits at each branch node, including surrogate splits. If you do not use surrogate splits, then the function takes the sum over the best splits found at each branch node.

• Estimates of predictor importance do not depend on the order of predictors if you use surrogate splits, but do depend on the order if you do not use surrogate splits.

• If you use surrogate splits, predictorImportance computes estimates before the tree is reduced by pruning (or merging leaves). If you do not use surrogate splits, predictorImportance computes estimates after the tree is reduced by pruning. Therefore, pruning affects the predictor importance for a tree grown without surrogate splits, and does not affect the predictor importance for a tree grown with surrogate splits.

Impurity and Node Error

A decision tree splits nodes based on either impurity or node error.

Impurity means one of several things, depending on your choice of the SplitCriterion name-value argument:

• Gini's Diversity Index (gdi) — The Gini index of a node is

  $$1-{\displaystyle \sum _i{p}^2(i)},$$

  where the sum is over the classes i at the node, and p(i) is the observed fraction of classes with class i that reach the node. A node with just one class (a pure node) has Gini index 0; otherwise, the Gini index is positive. So the Gini index is a measure of node impurity.

• Deviance ("deviance") — With p(i) defined the same as for the Gini index, the deviance of a node is

  $$-{\displaystyle \sum _{i}p(i){\log }_{2}p(i)}.$$

  A pure node has deviance 0; otherwise, the deviance is positive.

• Twoing rule ("twoing") — Twoing is not a purity measure of a node, but is a different measure for deciding how to split a node. Let L(i) denote the fraction of members of class i in the left child node after a split, and R(i) denote the fraction of members of class i in the right child node after a split. Choose the split criterion to maximize

  $$P(L)P(R){\left({\displaystyle \sum _i\left|L(i)-R(i)\right|}\right)}^2,$$

  where P(L) and P(R) are the fractions of observations that split to the left and right, respectively. If the expression is large, the split made each child node purer. Similarly, if the expression is small, the split made each child node similar to each other and, therefore, similar to the parent node. The split did not increase node purity.

• Node error — The node error is the fraction of misclassified classes at a node. If j is the class with the largest number of training samples at a node, the node error is

  1 – p(j).

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2011a