incrementalKMeans
Description
The incrementalKMeans function creates an
incrementalKMeans model object that is suitable for incremental
k-means clustering. Unlike the kmeans function, which requires you to provide all the data before computing the
cluster assignments, incrementalKMeans allows you to update the clustering
model incrementally by supplying chunks of data to the incremental fit function. To
perform incremental k-means clustering with a dynamically changing number
of clusters, use incrementalDynamicKMeans.
When you call the incrementalKMeans function you can specify clustering
options, such as the distance metric, the warm-up period, and whether to standardize the
training data before fitting the model to data. After you create an
incrementalKMeans object, it is prepared for incremental
k-means clustering. For more information, see Incremental k-Means Clustering.
Creation
You can create an incrementalKMeans model object in two ways:
Call the function directly — Configure incremental k-means clustering options by calling
incrementalKMeansdirectly. This approach is best when you do not have data yet or you want to start incremental k-means clustering immediately. When you callincrementalKMeans, you can specify cluster centroids and cluster counts so that the initial model is warm.Call an incremental learning function — The
fitandupdateMetricsfunctions accept a configuredincrementalKMeansmodel object and data as input, and return anincrementalKMeansmodel object updated with information computed from the input model and data.
Syntax
Description
Mdl = incrementalKMeans(numClusters=k)k and default model parameters.
Mdl = incrementalKMeans(centroids=C)C.
Mdl = incrementalKMeans(___,Name=Value)Mdl=incrementalKMeans(numClusters=2,Distance="cityblock") creates an
incrementalKMeans model object with two clusters using the city block
distance metric.
Input Arguments
Number of clusters, specified as a positive integer. This argument sets the
NumClusters
property.
If you specify k:
Example: 10
Data Types: single | double
Initial cluster centroids, specified as an
n-by-p numeric matrix where each row contains
a cluster centroid, and each column contains the predictor values. The software uses
C to set the initial values of the Centroids
property.
If you specify C:
Centroidscontains n rows.Centroidscontains the unique rows ofCand additional rows ofNaNvalues, ifCcontains nonunique rows.You cannot specify
korStandardizeData.The software sets
NumClusters=n andStandardizeData=false.You cannot specify a nonzero value of
NumPredictors. If you specifyNumPredictors=0, the software setsNumPredictorsequal to p.
Example: [2 4 5; 1 3 3; 2 5 1]
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Mdl =
incrementalKMeans(numClusters=13,EstimationPeriod=1000,StandardizeData=true)
creates the model object using 13 clusters, and to standardize the data using an
estimation period of 1000 observations.
Cluster counts, specified as a vector of positive integers. This argument sets
the initial value of the ClusterCounts property. The software updates this property when you
call the reset
function or the incremental fit
function. The incremental fit function uses
ClusterCounts to determine the learning rate when it updates
the cluster centroids.
If you specify ClusterCounts=counts when
you create Mdl:
You must specify
C.You cannot specify
k.You cannot specify
StandardizeData. The software setsStandardizeData=false.countsmust be a vector of positive integers with lengthsize(C,1).ClusterCountsis a column vector with lengthsize(.C,1)The first m rows of
ClusterCountscontain the sum of thecountsvalues for each of the m unique rows ofC. If C contains nonunique rows, the remaining rows ofClusterCountscontain zeros.
If you do not specify ClusterCounts when you create
Mdl:
ClusterCountsis ak-by-1 vector of zeros if you specifyk.ClusterCountsis asize(C,1)-by-1 vector if you specifyC. The first m rows ofClusterCountscontain the number of instances of each of the m unique rows inC. The remaining rows ofClusterCountscontain zeros.
Example: ClusterCounts=[2 4 9 2 5 2 6 7]
Data Types: single | double
Number of predictors, specified as a nonnegative integer. This argument sets the NumPredictors
property.
If you specify
Cwhen you createMdl:You can only specify
NumPredictors=size(orC,2)NumPredictors=0The software sets
NumPredictors=size(if you do not specifyC,2)NumPredictorsor specifyNumPredictors=0
If you specify
kand do not specifyNumPredictorswhen you createMdl, the software setsNumPredictors=0.If
NumPredictors=0, the software infers the number of predictors from the training data and updatesNumPredictorswhen you call the incrementalfitfunction.
Example: NumPredictors=10
Data Types: single | double
Distance metric in p-dimensional space used for minimization, where
p is the number of predictors in the training data, specified as
"sqeuclidean", "cityblock",
"cosine", or "correlation". The
incrementalKMeans function does not support the Hamming distance
metric. This argument sets the Distance property.
incrementalKMeans computes centroid clusters differently for the
supported distance metrics. This table summarizes the available distance metrics. In
each formula, x is an observation (that is, a row of
X) and c is a centroid (a row
vector).
| Distance Metric | Description | Formula |
|---|---|---|
"sqeuclidean" | Squared Euclidean distance (default). Each centroid is the mean of the points in the cluster. |
|
"cityblock" | Sum of absolute differences, that is, the L1 distance. Each centroid is the component-wise median of the points in the cluster. |
|
"cosine" | One minus the cosine of the included angle between points (treated as vectors). Each centroid is the mean of the points in the cluster, after the points are normalized to unit Euclidean length. |
|
"correlation" | One minus the sample correlation between points (treated as sequences of values). Each centroid is the component-wise mean of the points in the cluster, after the points are centered and normalized to zero mean and unit standard deviation. |
where
|
Example: Distance="cityblock"
Data Types: char | string
Forgetting factor for cluster centroid updates, specified as a scalar value from
0 to 1. This argument sets the ForgettingFactor
property.
A forgetting factor value of 0.1 gives more weight to the older
data than a forgetting factor value of 0.9. A forgetting factor value
of 0 indicates infinite memory, where all the previous observations
have equal weight when the incremental fit function updates the
cluster centroids.
Example: ForgettingFactor=0.1
Data Types: double | single
Number of observations to which the model must be fit before it is warm, specified as a
nonnegative integer. This argument sets the WarmupPeriod property.
When a model is warm, the incremental fit function returns
cluster indices, and the incremental updateMetrics function returns
performance metrics. When processing observations during the warm-up period, the
software ignores observations that contain at least one missing value. If you specify
C and ClusterCounts when you create
Mdl, and C contains no duplicate rows, then
IsWarm is
true and the default value of WarmupPeriod
is 0. Otherwise, the default value of
WarmupPeriod is 1000.
Note
IsWarm cannot be true if
Centroids contains any NaN values or
NumPredictors is 0.
Example: WarmupPeriod=100
Data Types: single | double
Performance metrics to track during incremental learning, specified as
"SimplifiedSilhouette". The Metrics
property of Mdl stores two forms of each performance metric as
variables (columns) of a table, Cumulative and
Window, with individual metrics in rows.
MetricsWindowSize determines the update frequency of the
Window metrics. For more details, see Estimation Period and Simplified Silhouette.
Example: Metrics="SimplifiedSilhouette"
Data Types: char | string
Number of observations to use to compute window performance metrics, specified
as a positive integer. The default value is 200. This argument
sets the MetricsWindowSize property.
For more details on performance metrics options, see Performance Metrics.
Example: MetricsWindowSize=100
Data Types: single | double
Flag to standardize the predictor data, specified as a numeric or logical 0
(false) or 1 (true).
If you specify StandardizeData=true, the incremental
fit function estimates the predictor means
Mu and standard deviations Sigma during the
estimation period specified by EstimationPeriod, and standardizes
the predictor data.
You cannot specify StandardizeData if you specify C.
For more information, see Standardize Data.
Example: StandardizeData=true
Data Types: single | double | logical
Number of observations processed by the incremental model to estimate the predictor
means and standard deviations, specified as a nonnegative integer. This argument sets
the EstimationPeriod
property.
If you specify StandardizeData=true, the
default value is 1000. Otherwise, the default value is
0.
If you specify EstimationPeriod when you create
Mdl:
The software sets
EstimationPeriod=0when you specifyCorStandardizeData=false.The software uses
EstimationPeriodobservations to estimate the predictor means (Mu) and standard deviations (Sigma) prior to training the model.The software ignores observations that contain at least one missing value when processing observations during the estimation period.
For more details, see Estimation Period.
Example: EstimationPeriod=500
Data Types: single | double
Properties
Training Parameters
This property is read-only.
Predictor means, represented as a numeric vector.
When you create
Mdland specifyNumPredictors=0orStandardizeData=false(the default), thenMuis an empty array[].When you create
Mdland setStandardizeData=true, specifyNumPredictorsas a positive integer, and specifyk, thenMuis initially a 1-by-NumPredictorsvector of zeros. Otherwise,Muis[].When you create
Mdland setStandardizeData=true, andMuis[]or an array of zeros, then the incrementalfitfunction calculates the predictor variable means using all data points that do not have any missing values. At the end of the estimation period specified byEstimationPeriod,Muis aNumPredictors-by-1 vector that contains the predictor means.
You cannot specify Mu directly.
Data Types: single | double
This property is read-only.
Predictor standard deviations, represented as a numeric vector.
When you create
Mdland specifyNumPredictors=0orStandardizeData=false(the default), thenSigmais an empty array[].When you create
Mdland setStandardizeData=true, specifyNumPredictorsas a positive integer, and specifyk, thenSigmais initially a 1-by-NumPredictorsvector of zeros. Otherwise,Sigmais[].When you create
Mdland setStandardizeData=true, andSigmais[]or an array of zeros, then the incrementalfitfunction calculates the predictor variable standard deviations using all data points that do not have any missing values. At the end of the estimation period specified byEstimationPeriod,Sigmais aNumPredictors-by-1 vector that contains the predictor standard deviations.
You cannot specify Sigma directly.
Data Types: single | double
This property is read-only after object creation.
Number of observations processed by the incremental model to estimate the predictor
means and standard deviations, represented as a nonnegative integer. If you specify
StandardizeData=true when you create
Mdl, the default value is 1000. Otherwise,
the default value is 0.
If EstimationPeriod
>
0:
The software uses
EstimationPeriodobservations to estimate the predictor means (Mu) and standard deviations (Sigma) prior to training the model.The software ignores observations that contain at least one missing value when processing observations during the estimation period.
For more details, see Estimation Period.
Data Types: single | double
This property is read-only after object creation.
Distance metric in p-dimensional space used for minimization, where
p is the number of variables in the training data, stored as
"sqeuclidean", "cityblock",
"cosine", or "correlation". For a description
of the supported distance metrics, see Distance. The incrementalKMeans function does not support
the Hamming distance metric.
Data Types: string
This property is read-only after object creation.
Forgetting factor for cluster centroid updates, represented as a scalar value
from 0 to 1. A forgetting factor value
of 0.1 gives more weight to the older data than a
forgetting factor value of 0.9. A forgetting factor value
of 0 indicates infinite memory, where all the previous
observations have equal weight when the incremental fit
function updates the cluster centroids.
Data Types: single | double
This property is read-only.
Number of observations fit to the incremental model Mdl, represented as a
nonnegative numeric scalar. NumTrainingObservations increases when
you pass Mdl and training data to the incremental
fit function outside of the estimation period. The software
resets NumTrainingObservations to 0 when you call
the reset function.
When fitting the model, the software ignores observations that contain at least one missing value.
You cannot specify NumTrainingObservations directly.
Data Types: double
Clustering Parameters
This property is read-only after object creation.
Number of predictors, represented as a nonnegative integer.
If you specify
Cwhen you createMdland do not specifyNumPredictors, or specifyNumPredictors=0NumPredictors=size(.C,2)If you specify
kwhen you createMdland do not specifyNumPredictors, the initial value ofNumPredictorsis0.If
NumPredictors=0, the software infers the number of predictors from the training data and updatesNumPredictorswhen you call the incrementalfitfunction.
Data Types: single | double
This property is read-only after object creation.
Number of clusters, represented as a positive integer. If you do not specify
k when you create Mdl, then
NumClusters is equal to size(C,1). The
software updates NumClusters when you call the
reset function or the incremental fit
function.
Data Types: single | double
This property is read-only after object creation.
Cluster centroids, represented as a
NumClusters-by-NumPredictors numeric
matrix where each row contains a cluster centroid, and each column contains the
predictor values. The software updates Centroids when you call
the reset function or the incremental fit
function.
If you do not specify C when you create
Mdl:
Centroidsis initially ak-by-NumPredictorsarray ofNaNvalues.When you call the incremental
fitfunction with predictor dataX:If
NumPredictors=0, the function resizesCentroidsto have the same number of columns asX.If
Centroidshas i rows ofNaNvalues, the function sets their values equal to the first i observations inX.
Data Types: single | double
This property is read-only after object creation.
Cluster counts, represented as a NumClusters-by-1 numeric
vector. The software updates ClusterCounts when you call the
reset function or the incremental fit
function. The incremental fit function uses
ClusterCounts to determine the learning rate when it updates
the cluster centroids. If ForgettingFactor is
0, then the values of ClusterCounts are
1 + the number of observations assigned to each cluster.
Otherwise, the values of ClusterCounts represent the relative
sizes of each cluster.
If you specify ClusterCounts=counts when
you create Mdl:
ClusterCountsis a column vector with lengthsize(.C,1)The first m rows of
ClusterCountscontain the sum of thecountsvalues for each unique row ofC, if C contains nonunique rows and m unique rows. The remaining rows ofClusterCountscontain zeros.
If you do not specify ClusterCounts when you create
Mdl:
ClusterCountsis ak-by-1 vector of zeros, if you specifyk.ClusterCountsis asize(C,1)-by-1 vector, if you specifyC. The first m rows ofClusterCountscontain ones, where m is the number of unique rows inC. The remaining rows ofClusterCountscontain zeros.
Data Types: single | double
Performance Metrics Parameters
This property is read-only.
Flag indicating whether the incremental fit function returns cluster
indices and the incremental updateMetrics function returns
performance metrics, represented as a numeric or logical 0
(false) or 1 (true).
IsWarm becomes true after the incremental fit function fits the incremental model to WarmupPeriod observations. However, IsWarm cannot be true if Centroids contains any NaN values or NumPredictors is 0.
If IsWarm is false:
The
idxoutput offitconsists ofNaNvalues.The
updateMetricsfunction storesNaNvalues inMetrics.
If Mdl.EstimationPeriod > 0, then during the estimation period:
IsWarmisfalse.The value of
NumTrainingObservationsis0.The
fitfunction does not fit the model.The
updateMetricsfunction does not store any values inMetrics.
You cannot specify IsWarm directly.
Data Types: single | double | logical
This property is read-only after object creation.
Number of observations to which the model must be fit before it is warm, represented
as a nonnegative integer. When a model is warm, the incremental fit
function returns cluster indices, and the incremental updateMetrics
function returns performance metrics. When processing observations during the warm-up
period, the software ignores observations that contain at least one missing value. If
you specify both C and ClusterCounts when you
create Mdl, and C contains no duplicate rows,
then IsWarm=true and the default value of
WarmupPeriod is 0. Otherwise, the default
value of WarmupPeriod is 1000.
Note
IsWarm cannot be true if
Centroids contains any NaN values or
NumPredictors is 0.
Data Types: single | double
This property is read-only.
Model performance metrics updated during incremental learning by
updateMetrics, represented as a table with two columns labeled
Cumulative and Window.
Cumulative— Model performance, as measured by the Simplified Silhouette metric, from the time the model becomes warm (IsWarmis1).Window— Model performance, as measured by the simplified silhouette metric, evaluated over all observations within the window specified by theMetricsWindowSizeproperty. The software updatesWindowafter it processesMetricsWindowSizeobservations.
The software sets Metrics to NaN when you
call the reset function.
You cannot specify Metrics directly.
Data Types: table
This property is read-only after object creation.
Number of observations to use to compute window performance metrics, represented as a positive integer. The default value is 200.
For more details on performance metrics options, see Performance Metrics.
Data Types: single | double
Object Functions
fit | Fit model for incremental k-means clustering |
updateMetrics | Update performance metrics in incremental k-means clustering model given new data |
assignClusters | Assign observations to existing clusters |
reset | Reset incremental k-means clustering model |
Examples
Create an incremental model for k-means clustering that has two clusters.
Mdl = incrementalKMeans(numClusters=2)
Mdl =
incrementalKMeans
IsWarm: 0
Metrics: [1×2 table]
NumClusters: 2
Centroids: [2×0 double]
Distance: "sqeuclidean"
Properties, Methods
Mdl is an incrementalKMeans model object. All its properties are read-only.
Load and Preprocess Data
Load the New York city housing data set.
load NYCHousing2015.matThe data set includes 10 variables with information on the sales of properties in New York City in 2015. Keep only the gross square footage and sale price predictors. Keep all records that have a gross square footage above 100 square feet and a sales price above $1000.
data = NYCHousing2015(:,{'GROSSSQUAREFEET','SALEPRICE'});
data = data((data.GROSSSQUAREFEET > 100 & data.SALEPRICE > 1000),:);Convert the tabular data into a matrix that contains the logarithm of both predictors.
X = table2array(log10(data));
Randomly shuffle the order of the records.
rng(0,"twister"); % For reproducibility X = X(randperm(size(X,1)),:);
Fit and Plot Incremental Model
Fit the incremental model Mdl to the data by using the fit function. To simulate a data stream, fit the model in chunks of 500 records at a time. At each iteration:
Process 500 observations.
Overwrite the previous incremental model with a new one fitted to the incoming records.
Update the performance metrics for the model. The default metric for
MdlisSimplifiedSilhouette.Store the cumulative and window metrics to see how they evolve during incremental learning.
Compute the cluster assignments of all records seen so far, according to the current model.
Plot all records seen so far, and color each record by its cluster assignment.
Plot the current centroid location of each cluster.
In this workflow, the updateMetrics function provides information about the model's clustering performance after it is fit to the incoming data chunk. In other workflows, you might want to evaluate a clustering model's performance on unseen data. In such cases, you can call updateMetrics prior to calling the incremental fit function.
% Initialize plot properties hold on h1 = scatter(NaN,NaN,0.3); h2 = plot(NaN,NaN,Marker="o", ... MarkerFaceColor="k",MarkerEdgeColor="k"); h3 = plot(NaN,NaN,Marker="^", ... MarkerFaceColor="b",MarkerEdgeColor="b"); colormap(gca,"prism") pbaspect([1,1,1]) xlim([min(X(:,1)),max(X(:,1))]); ylim([min(X(:,2)),max(X(:,2))]); xlabel("log Gross Square Footage"); ylabel("log Sales Price in Dollars") % Incremental fitting and plotting n = numel(X(:,1)); numObsPerChunk = 500; nchunk = floor(n/numObsPerChunk); sil = array2table(zeros(nchunk,2),VariableNames=["Cumulative" "Window"]); for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = fit(Mdl,X(idx,:)); Mdl = updateMetrics(Mdl,X(idx,:)); sil{j,:} = Mdl.Metrics{'SimplifiedSilhouette',:}; indices = assignClusters(Mdl,X(1:iend,:)); title("Iteration " + num2str(j)) set(h1,XData=X(1:iend,1),YData=X(1:iend,2),CData=indices); set(h2,Marker="none") % Erase previous centroid markers set(h3,Marker="none") set(h2,XData=Mdl.Centroids(1,1),YData=Mdl.Centroids(1,2),Marker="o") set(h3,Xdata=Mdl.Centroids(2,1),YData=Mdl.Centroids(2,2),Marker="^") pause(0.5); end
Warning: Hardware-accelerated graphics is unavailable. Displaying fewer markers to preserve interactivity.
hold off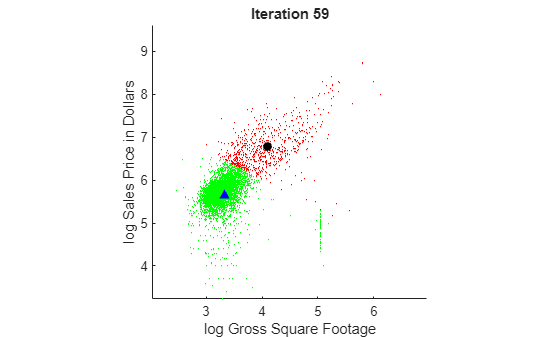
To view the animated figure, you can run the example, or open the animated gif below in your web browser.

At each iteration, the animated plot displays all the observations processed so far as small circles, and colors them according to the cluster assignments of the current model. The black circle indicates the centroid position of cluster 1, and the blue triangle indicates the centroid position of cluster 2.
Plot the window and cumulative metrics values at each iteration.
h4 = plot(sil.Variables); xlabel("Iteration") ylabel("Performance Metric") xline(Mdl.WarmupPeriod/numObsPerChunk,'g-.') legend(h4,sil.Properties.VariableNames,Location="southeast")
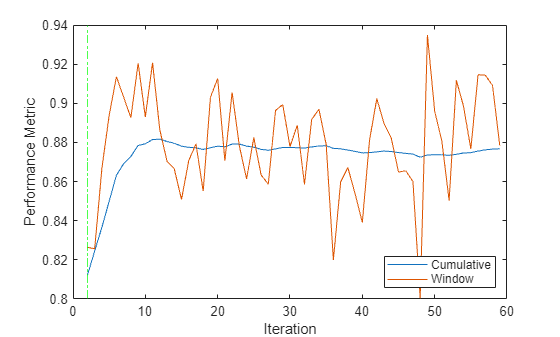
The updateMetrics function calculates the performance metrics after the end of the warm-up period. The performance metrics rise rapidly from an initial value of 0.81 and approach a value of approximately 0.88 after 10 iterations.
Create a set of noisy position measurements of two moving objects. Object 1 starts at (x,y) coordinate (-50,0) and moves along the x-axis. Object 2 starts at (x,y) coordinate (0,-40) and moves along the y-axis. The objects move at the same speed.
Generate numObsPerStep=100 measurements of each object at numSteps=100 individual time steps.
rng(0,"twister") % For reproducibility sigma = 2; % Measurement noise level numObsPerStep = 100; numSteps = 100; startPosA = [-50,0]; startPosB = [0,-40]; X = []; for t = 0:numSteps-1 for i = 1:numObsPerStep p = randn(1,4)*sigma; % Gaussian measurement noise X = [X;[[p(1)+t+startPosA(1);p(2)+startPosB(1)], ... [p(3)+startPosA(2);p(4)+t+startPosB(2)]]]; end end
The rows of X contain 2*numObsPerStep*numSteps position measurements. The columns of X contain the x and y coordinates of each measurement, respectively.
Create Incremental k-Means Clustering Models
To track the centroids of the moving clusters, create two incremental k-means clustering model objects that each have two clusters and no warm-up period. Specify a forgetting factor value of 0.1 for the first model, and 0.75 for the second model. A lower value of the forgetting factor (which can range from 0 to 1) assigns more weight to older measurements when the incremental fit algorithm calculates new cluster centroids.
MdlA = incrementalKMeans(numClusters=2,WarmupPeriod=0, ... ForgettingFactor=0.1); MdlB = incrementalKMeans(numClusters=2,WarmupPeriod=0, ... ForgettingFactor=0.75);
Fit and Plot Incremental Models
Fit the incremental k-means clustering models to the data by using the fit function. Fit the models in data chunks that consist of the measurements at each time step. At each iteration:
Process
2*numObsPerStepobservations.Overwrite the previous incremental models with new ones fitted to the incoming measurements.
Update the performance metrics for the models. The metric for the models is
SimplifiedSilhouette.Store the cumulative and window metrics to see how they evolve during incremental learning.
Compute the cluster assignments of the incoming chunk of measurements, according to the current model A.
Plot the incoming chunk of measurements, and color each measurement by its cluster assignment according to model A.
Plot the current model centroid locations for each cluster.
Plot all of the previous measurements using gray points.
% Initialize plot properties hold on h1 = scatter(NaN,NaN,0.2,[0.9 0.9 0.9],"."); h2 = scatter(NaN,NaN,1.5); h3 = plot(NaN,NaN,"^",MarkerSize=6,MarkerEdgeColor="k", ... MarkerFaceColor="k"); h4 = plot(NaN,NaN,"square",MarkerSize=6,MarkerEdgeColor="b", ... MarkerFaceColor="b"); colormap(gca,"prism") xlim([min(X(:,1)),max(X(:,1))]); ylim([min(X(:,2)),max(X(:,2))]); xlabel("X"); ylabel("Y"); % Incremental fitting and plotting n = numel(X(:,1)); nChunk = 2*numObsPerStep; silA = array2table(zeros(numSteps,2), ... 'VariableNames',["Cumulative" "Window"]); silB = array2table(zeros(numSteps,2), ... 'VariableNames',["Cumulative" "Window"]); for j = 1:numSteps ibegin = min(n,nChunk*(j-1) + 1); iend = min(n,nChunk*j); idx = ibegin:iend; [MdlA,indices] = fit(MdlA,X(idx,:)); MdlA = updateMetrics(MdlA,X(idx,:)); MdlB = fit(MdlB,X(idx,:)); MdlB = updateMetrics(MdlB,X(idx,:)); title("Iteration " + num2str(j)) silA{j,:} = MdlA.Metrics{'SimplifiedSilhouette',:}; silB{j,:} = MdlB.Metrics{'SimplifiedSilhouette',:}; set(h1,XData=X(1:ibegin-1,1),YData=X(1:ibegin-1,2)); set(h2,XData=X(idx,1),YData=X(idx,2),CData=indices); set(h3,Marker="none") % Erase the previous centroid markers set(h4,Marker="none") set(h3,XData=MdlA.Centroids(:,1),YData=MdlA.Centroids(:,2), ... Marker="^"); set(h4,XData=MdlB.Centroids(:,1),YData=MdlB.Centroids(:,2), ... Marker="square"); pause(0.2); end hold off

 At each iteration, the animated plot displays all of the position measurements processed so far in gray. The incremental
At each iteration, the animated plot displays all of the position measurements processed so far in gray. The incremental fit function tracks the centroid of each object at each iteration. The measurements in the current data chunk are colored according to the cluster assignment of model A. The black upward-pointing triangles and blue squares indicate the fitted cluster centroids of models A and B, respectively.
Model A does a good job of tracking the true position of each moving object. Because model B has a higher forgetting factor, the fit function assigns the highest weights to the most recent measurements. Therefore, model B does a poorer job of tracking the true positions of the objects.
Plot the simplified silhouette performance metrics at each iteration.
h5 = plot([silA.Variables,silB.Variables]); xlabel("Iteration") ylabel("Simplified Silhouette") legend(h5,{"Cumulative A","Window A", ... "Cumulative B","Window B"},Location="southwest")
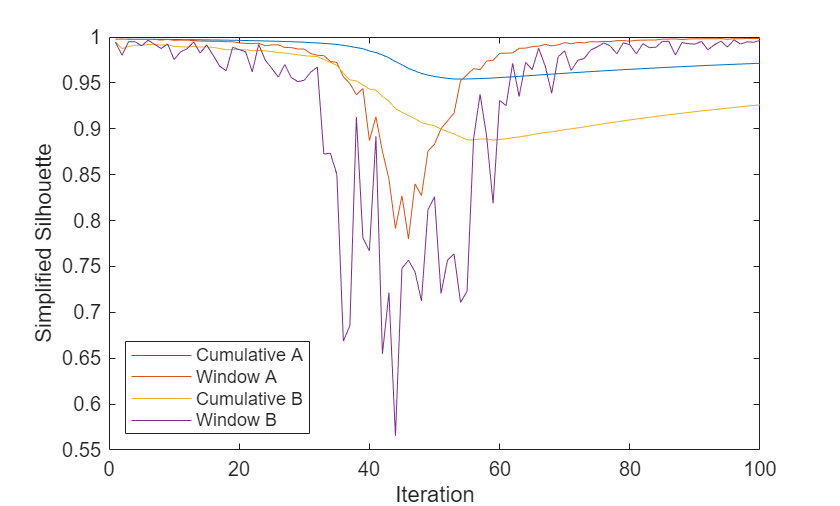
The plot shows that the simplified silhouette values of model B are poorer than those of model A. The values of both models dip significantly between iterations 30 and 60, when the two objects are close to each other. As the objects move apart, the window values of both models return to their previous levels.
Generate a training data set using three distributions.
rng(0,"twister") % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2); randn(100,2)*0.75];
Train a k-means clustering model on the batch of data using kmeans with the city block distance metric.
dist = "cityblock";
[idx,C] = kmeans(X,3,Distance=dist);Compute the number of data points in each cluster.
countTable = tabulate(idx); counts = countTable(:,2)
counts = 3×1
84
103
113
Plot the clusters and the cluster centroids.
hold on gscatter(X(:,1),X(:,2),idx,"bgm") plot(C(:,1),C(:,2),"kx",Markersize=10) legend("Cluster 1","Cluster 2","Cluster 3","Cluster centroid") hold off

Create an incremental model for k-means clustering that uses the same distance metric. Initialize the incremental model object using the centroids and cluster counts from the fitted batch k-means model.
Mdl = incrementalKMeans(centroids=C,ClusterCounts=counts,Distance=dist); details(Mdl)
incrementalKMeans with properties:
Mu: []
Sigma: []
EstimationPeriod: 0
Centroids: [3×2 double]
ClusterCounts: [3×1 double]
Distance: "cityblock"
ForgettingFactor: 0.0500
NumClusters: 3
IsWarm: 1
NumTrainingObservations: 0
NumPredictors: 2
WarmupPeriod: 0
Metrics: [1×2 table]
MetricsWindowSize: 200
Methods, Superclasses
Mdl is an incrementalKMeans model object. All its properties are read-only. Because Mdl is warm, when you pass the model and streaming data to the incremental fit and updateMetrics functions, they return cluster indices and performance metrics, respectively.
More About
The k-means clustering algorithm [1] is a data-partitioning algorithm that assigns observations (points) to exactly one of
k clusters defined by centroids, where k is
specified before the algorithm starts. The incremental k-means
fit function uses a gradient descent method based on the algorithm in
[2] to minimize the sum of
point-to-centroid distances, summed over all k clusters. When you call
fit with an incrementalKMeans model object
Mdl and a batch of data X:
If
Mdlhas i missing centroid locations, the function sets their locations equal to the first i unique observations inX.The function finds cluster indices for all the observations in
Xusing the current centroid locations. The cluster index of each observation corresponds to the closest cluster centroid according to the distance metric inMdl.The function updates each cluster centroid p using the following steps:
Compute gradients using the distance between each observation and the centroid p.
Update the
ClusterCountvalueCCpfor cluster p using the formulaCCp,new=(1-ForgettingFactor)*CCp+Cp, whereCpis the number of observations inXthat have cluster index p according to the current model.Use 1/
CCp,newas the learning rate for the gradient descent update.Update the cluster centroid p by looping over each observation with cluster index p, using the computed gradient for each observation.
The updateMetrics
function tracks model performance metrics (Metrics) from new data when
the incremental model is warm (Mdl.IsWarm property). An incremental model
becomes warm after fit fits the
incremental model to WarmupPeriod observations, which is the
warm-up period.
If Mdl.EstimationPeriod > 0, the software estimates the predictor
means and standard deviations before fitting the model to data. Therefore, the software must
process an additional EstimationPeriod observations before the model
starts the warm-up period.
The Metrics property of the incremental model stores two forms of
each performance metric as variables (columns) of a table, Cumulative and
Window, with individual metrics in rows. When the incremental model is
warm, updateMetrics updates the metrics at the following frequencies:
Cumulative— The function computes cumulative metrics since the start of model performance tracking. The function updates metrics every time you call it, and bases the calculation on the entire supplied data set until a model reset.Window— The function computes metrics based on all observations within a window determined by theMetricsWindowSizename-value argument.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMetricsWindowSizeis 20, the function computes metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store
MetricsWindowSizeamount of values for each specified metric.Populate elements of the metrics values with the model performance based on batches of incoming observations.
When the window of observations is filled, overwrite
Mdl.Metrics.Windowwith the average performance in the metrics window. If the window is overfilled when the function processes a batch of observations, the latest incomingMetricsWindowSizeobservations are stored, and the earliest observations are removed from the window. For example, supposeMetricsWindowSizeis 20, the window contains 10 stored values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a NaN cluster index when
computing the Cumulative and Window performance metric
values.
If incremental learning functions are configured to standardize predictor variables, they
do so using the means and standard deviations stored in the Mu and
Sigma properties, respectively, of the incremental learning model
Mdl. The incremental fit function estimates
means and standard deviations using the estimation period observations when:
You specify
StandardizeData=truewhen you createMdlMdl.EstimationPeriodis positive (see Estimation Period).Mdl.Muis[]or an array of zeros, andMdl.Sigmais[]or an array of ones.
During the estimation period, the incremental fit function does not
fit the model. The function uses the first incoming EstimationPeriod
observations to estimate the variable means and standard deviations. At the end of the
estimation period, the function updates the Mu and
Sigma properties of the model.
Estimation occurs only when:
You specify
StandardizeData=truewhen you createMdl.Mdl.EstimationPeriodis positive.Mdl.Muis[]or an array of zeros, andMdl.Sigmais[]or an array of ones.
The simplified silhouette value si for the ith point is defined as
where ap,i is the distance of
the ith point to the centroid of its cluster p[3].
bp,i is the distance of the
ith point to the centroid of its closest neighboring cluster. If the
ith point is the only point in its cluster, then the simplified
silhouette value of the point is 1.
The simplified silhouette values range from –1 to 1.
A high value indicates that the point is well matched to its own cluster and poorly matched
to other clusters. If most points have a high simplified silhouette value, then the
clustering solution is appropriate. If many points have a low or negative simplified
silhouette value, then the clustering solution might have too many or too few clusters. You
can use simplified silhouette values as a clustering evaluation criterion with any distance
metric. By default, the performance metric values stored in the model object are the average
simplified silhouette values for all points passed to the updateMetrics
function.
Tips
You can create an
incrementalKMeansmodel object that incorporates the outputs of thekmeansfunction by using the following code:k = 2; [idx,C]=kmeans(X,k); countTable = tabulate(idx); counts = countTable(:,2) Mdl = incrementalKMeans(centroids=C,ClusterCounts=counts);
References
[1] Lloyd, S. Least Squares Quantization in PCM. IEEE Transactions on Information Theory 28, no. 2 (March 1982): 129–37.
[2] Sculley, D. Web-Scale k-Means Clustering. In Proceedings of the 19th International Conference on World Wide Web, 1177–78. Raleigh North Carolina USA: ACM, 2010.
[3] Vendramin, Lucas, Ricardo J.G.B. Campello, and Eduardo R. Hruschka. On the Comparison of Relative Clustering Validity Criteria. In Proceedings of the 2009 SIAM international conference on data mining, 733–744. Society for Industrial and Applied Mathematics, 2009.
Version History
Introduced in R2025a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)