La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Synchrosqueezing des ondelettes

Qu’est-ce que le synchrosqueezing des ondelettes ?

La transformée par synchrosqueezing en ondelettes est une méthode d'analyse temps-fréquence utile pour analyser les signaux à composantes multiples avec des modes d’oscillation. Les formes d'onde de la parole, les vibrations des machines et les signaux physiologiques sont des exemples de signaux présentant des modes d'oscillation. Beaucoup de ces signaux du monde réel avec des modes oscillants peuvent être écrits comme une somme de composantes modulées en amplitude et en fréquence. Une expression générale pour ces types de signaux à composantes additionnées est

$${\displaystyle \sum _{k=1}^K{A}_k(t)\cos (2\pi {\varphi }_k(t))},$$

où $$A_k(t)$$ est l'amplitude à variation lente et $${\varphi }_k(t)$$ est la phase instantanée. Une série de Fourier tronquée, où l'amplitude et la fréquence ne varient pas dans le temps, est un cas particulier de ces signaux.

La transformée en ondelettes et d'autres méthodes d'analyse linéaire temps-fréquence décomposent ces signaux en leurs composantes en corrélant le signal avec un dictionnaire d'atomes temps-fréquence [1]. La transformée en ondelettes utilise des versions traduites et mises à l'échelle d'une ondelette mère comme atome temps-fréquence. Un certain étalement de la fréquence temporelle est associé à tous ces atomes de fréquence temporelle, ce qui affecte la netteté de l'analyse du signal.

La transformée de synchrosqueezing en ondelettes est une méthode temps-fréquence qui réaffecte l'énergie du signal en fréquence. Cette réaffectation compense les effets d'étalement causés par l'ondelette mère. Contrairement à d'autres méthodes de réaffectation temps-fréquence, le synchrosqueezing réaffecte l'énergie uniquement dans la direction de la fréquence, ce qui préserve la résolution temporelle du signal. En préservant le temps, l'algorithme de synchrosqueezing inverse peut reconstruire une représentation précise du signal original. Pour utiliser le synchrosqueezing, chaque terme de l'expression du signal des composantes additionnées doit être une fonction de type mode intrinsèque (IMT). Pour plus de détails sur les critères qui constituent les IMT, voir [2].

Algorithme de synchrosqueezing des ondelettes

L'algorithme de synchrosqueezing utilise les étapes suivantes.

1. Sélectionnez une ondelette analytique $$\psi (t)$$. Pour être utilisée avec le synchrosqueezing, la CWT doit utiliser une ondelette à valeurs complexes pour capturer les informations de fréquence instantanée.

2. Utilisez l’ondelette pour obtenir la CWT du signal d'entrée $$f(t)$$ : $$W_{\psi }f(s,u)$$. Les variables s et u désignent respectivement les paramètres d'échelle et de translation.

3. Extraire les fréquences instantanées de la sortie CWT, , en utilisant une transformée de phase, $${\omega }_f$$. Cette transformée de phase est proportionnelle à la première dérivée de la CWT par rapport à la translation, u. Les échelles sont définies en tant que $$s=\frac{{\omega }_0}{\omega }$$, où $${\omega }_0$$ est la fréquence de crête de l’ondelette et ω est la fréquence.

4. « Squeezer» la CWT sur les régions où la transformée de phase est constante. La valeur de fréquence instantanée qui en résulte est réaffectée à une valeur unique au centroïde de la région temps-fréquence CWT. Cette réaffectation se traduit par une sortie plus nette de la transformée par synchrosqueezing par rapport à la CWT.

Comme décrit, le synchrosqueezing utilise la transformée en ondelettes continue (CWT) et sa première dérivée par rapport à la translation. La CWT est inversible et comme la transformée de synchrosqueezing hérite de la propriété d'inversibilité de la CWT, le signal peut être reconstruit.

Illustration : Extraction de fréquence instantanée

Vous pouvez exprimer la CWT de la fonction $$f(t)$$ par rapport à l’ondelette$$\psi (t)$$ en utilisant la transformée de Fourier inverse du produit de la transformée de Fourier de la fonction et la transformée de Fourier de l’ondelette :

$$W_{\psi }f(s,u)={\displaystyle \int e^{2\pi i\omega u}}\widehat{f}(\omega )\overline{\widehat{\psi }(s\omega )}d\omega ,$$

où la barre au-dessus de $$\widehat{\psi }(s\omega )$$ désigne le conjugué complexe.

Considérez une simple exponentielle complexe, $$f(t)=e^{2\pi i\alpha t}$$. Pour extraire la fréquence instantanée de $$f(t)$$ :

1. Obtenez la transformée en ondelettes de la fonction :

   $$W_{\psi }f(s,u)=e^{2\pi i\alpha u}\overline{\widehat{\psi }(s\alpha )},$$

   où $$\widehat{\psi }(s\alpha )$$ est la transformée de Fourier de l'ondelette à $$s\alpha$$.

2. Prenez la dérivée partielle de l'équation précédente par rapport à la translation, u:

   $$\frac{\partial }{\partial u}{W}_{\psi }f(s,u)=2\pi i\alpha e^{2\pi i\alpha u}\overline{\widehat{\psi }(s\alpha )}.$$

3. Appliquez la définition de la transformée de phase $${\omega }_f(s,u)$$ (étape 3 dans Algorithme de synchrosqueezing des ondelettes) pour obtenir la fréquence instantanée : $${\omega }_f(s,u)=\alpha$$.

Séparation requise des composantes

Dans le cas du synchrosqueezing, les composantes du signal doivent être des IMT bien séparés dans le plan temps-fréquence. Si cette condition est remplie, vous pouvez suivre la trajectoire des fréquences instantanées le long d'une courbe. Les courbes montrent l'emplacement de l'énergie maximale telle qu'elle varie dans le temps pour chaque mode de signalisation. Voir wsstridge pour une description de l'algorithme des courbes de trajectoire.

Cette inégalité définit le critère de séparation requis :

$$\left|{\varphi }_k^{\text{'}}(t)-{\varphi }_{k-1}^{\text{'}}(t)\right|\ge \frac{1}{4}\left|{\varphi }_k^{\text{'}}(t)+{\varphi }_{k-1}^{\text{'}}(t)\right|$$

où $${\varphi }^{\text{'}}$$ est la fréquence instantanée et d est une constante de séparation positive [2]. Pour déterminer cette séparation requise, supposons qu'une ondelette bump, x, a une transformée de Fourier avec un support dans la plage $$\left[{\epsilon }_x-\Delta ,{\epsilon }_x+\Delta \right]$$. L’ondelette bump ayant une fréquence centrale de $$\frac{5}{2\pi }$$ Hz, utilisez $$\left[\frac{5}{2}\pi -\frac{1}{2},\frac{5}{2}\pi +\frac{1}{2}\right]$$ comme intervalle. Ensuite, résolvez $$\Delta <{\epsilon }_x\frac{d}{1+d}$$ pour d pour obtenir $$d>\frac{1}{4}$$ pour l'ondelette bump.

Pour illustrer cette exigence de séparation pour l'ondelette bump, considérons un signal composé de $$\cos (2\pi (0.1t))+\sin ((2\pi (0.2t))$$. En utilisant l'ondelette bump pour obtenir le CWT, la phase instantanée du cosinus est $${\varphi }_1(t)=0.1t$$, et la fréquence instantanée est la première dérivée, 0,1. De même, pour la composante sinus, la fréquence instantanée est de 0,2. L'inégalité de séparation, $$\left|0.1\right|\ge \frac{1}{4}\left|0.3\right|$$, est vraie. Par conséquent, les deux composantes du signal sont des fonctions d'IMT et sont suffisamment séparées pour utiliser la transformée de synchrosqueezing.

Si vous utilisez des fréquences plus élevées, comme 0,3 et 0,4 pour les fréquences instantanées, l'inégalité est $$\left|0.1\right|\ge \frac{1}{4}\left|0.7\right|$$, ce qui est faux. Ces composantes du signal n’étant pas des IMT bien séparés, le signal, $$\cos (2\pi (0.3t))+\sin ((2\pi (0.4t))$$, n'est pas approprié pour être utilisé avec la transformée de synchrosqueezing.

Exemples

Étalement par CWT ou transformée de synchrosqueezing

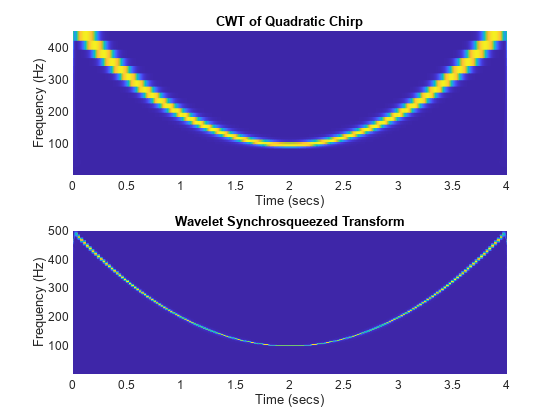
La comparaison de la CWT avec la transformée de synchrosqueezing d'un chirp quadratique montre un étalement d'énergie réduit pour le résultat de la transformée de synchrosqueezing.

load quadchirp
Fs = 1000;
[wt,f] = cwt(quadchirp,"bump",Fs);
subplot(2,1,1)
hp = pcolor(tquad,f,abs(wt));
hp.EdgeColor = "none";
xlabel("Time (secs)")
ylabel("Frequency (Hz)")
title("CWT of Quadratic Chirp")
subplot(2,1,2)
wsst(quadchirp,Fs,"bump")

Séparation des composantes basse et haute fréquences

Cet exemple montre la séparation nécessaire entre les composantes du signal pour obtenir des résultats utilisables à partir de la transformée de synchrosqueezing. Les composantes du signal sont de 0,025, 0,05, 0,20 et 0,225 cycles par échantillon. Les composantes haute fréquence, 0,20 et 0,225, ne sont pas suffisamment séparées, de sorte que vous ne pouvez pas exprimer le signal entier comme une somme d'IMT bien séparés.

Définissez le signal et tracez les composantes de synchrosqueezing.

t = 0:2000;
x1 = cos(2*pi*.025*t);
x2 = cos(2*pi*.05*t);
x3 = cos(2*pi*.20*t);
x4 = cos(2*pi*.225*t);
x =x1+x2+x3+x4;
[sst,f] = wsst(x);
contour(t,f,abs(sst))
xlabel("Time")
ylabel("Normalized Frequency")
title("Inadequate High-Frequency Separation")

Augmenter la séparation des composantes haute fréquence, puis tracer à nouveau les composantes de synchrosqueezing.

x4 = cos(2*pi*.3*t);
x =x1+x2+x3+x4;
[sst,f] = wsst(x);
contour(t,f,abs(sst))
xlabel("Time")
ylabel("Normalized Frequency")
title("Adequate High-Frequency Separation")

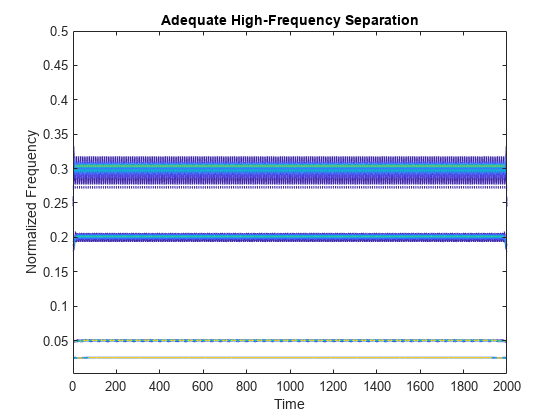
Toutes les composantes du signal sont maintenant des IMT bien séparés et sont suffisamment séparées pour être distinguées les unes des autres. Ce signal est approprié pour être utilisé avec l'algorithme de synchrosqueezing.

Région avec une séparation inadéquate

Cet exemple montre un signal avec deux chirps linéaires. Un chirp linéaire est défini comme

$$f(t)=\cos (\varphi +2\pi (f_{0}t+\frac{m{t}^2}{2})).$$

Sa première dérivée, $$f_0+mt$$, définit la ligne de fréquence instantanée. Utilisez l'ondelette bump et sa constante de séparation de 0,25. Pour déterminer la région où les deux signaux chirp avec des fréquences instantanées de 0,4 et 0,1 cycles par échantillon ne sont pas suffisamment séparés, résolvez cette équation :

$$|y_1-y_2|=0.25|y_1+y_2|.$$

$$y_1=\frac{-0.15}{1000}x+0.4$$ et $$y_2=\frac{0.15}{1000}x+0.1$$ sont les lignes de fréquence instantanée des chirps.

t = 0:2000;
y1 = chirp(t,0.4,1000,0.25);
y2 = chirp(t,0.1,1000,0.25);
y = y1+y2;
wsst(y,'bump')
xlabel('Samples')
h1 = line([583 583], [0 0.5]);
h2 = line([1417 1417], [0 0.5]);
h1.Color='white';
h2.Color='white';

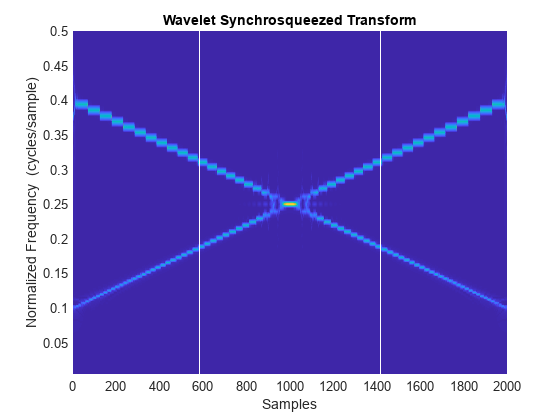
Les lignes verticales sont les limites de la région. Elles indiquent qu'il n'y a pas assez de séparation aux échantillons 583 et 1417. Dans la région entre les lignes verticales, le signal n'est pas constitué d'IMT bien séparés. Dans les régions situées en dehors des lignes verticales, le signal présente des IMT bien séparés. Vous pouvez obtenir de bons résultats avec la transformée de synchrosqueezing dans ces régions.

Références

[1] Mallet, S. A Wavelet Tour of Signal Processing. San Diego, CA: Academic Press, 2008, p. 89.

[2] Daubechies, I., J. Lu, and H. T. Wu. "Synchrosqueezed Wavelet Transforms: an empirical mode decomposition-like tool." Applied and Computational Harmonic Analysis. Vol. 30(2), pp. 243–261.

[3] Thakur, G., E. Brevdo, N. S. Fučkar, and H. T. Wu. "The synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications." Signal Processing. Vol. 93, pp. 1079–1094.

Sujets associés

• Time-Frequency Reassignment and Mode Extraction with Synchrosqueezing