Main Content

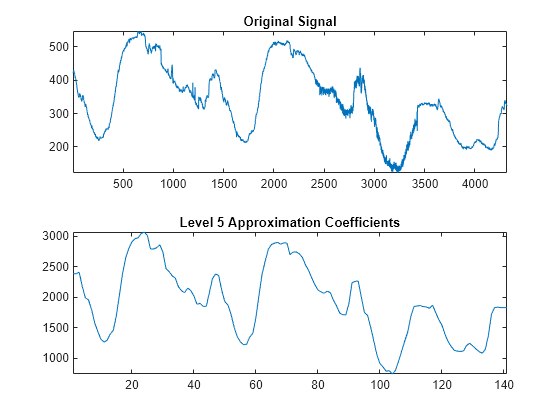
appcoef

1-D approximation coefficients

collapse all in page

Syntax

A = appcoef(C,L,wname)
A = appcoef(C,L,LoR,HiR)
A = appcoef(___,N)

Description

A = appcoef(C,L,wname) returns the approximation coefficients at the coarsest scale using the wavelet decomposition structure [C,L] of a 1-D signal and the wavelet specified by wname. (See wavedec for more information.)

A = appcoef(C,L,LoR,HiR) uses the lowpass reconstruction filter LoR and highpass reconstruction filter HiR. (See wfilters for more information.)

example

A = appcoef(___,N) returns the approximation coefficients at level N. If [C,L] is the M-level wavelet decomposition structure of a 1-D signal, then 0 ≤ N ≤ M.

Examples

collapse all

Open Live Script

This example shows how to extract the level 3 approximation coefficients.

Load the signal consisting of electricity usage data.

load leleccum; 
sig = leleccum(1:3920);

Obtain the DWT down to level 5 with the 'sym4' wavelet.

[C,L] = wavedec(sig,5,'sym4');

Extract the level-3 approximation coefficients. Plot the original signal and the approximation coefficients.

Lev = 3;
a3 = appcoef(C,L,'sym4',Lev);
subplot(2,1,1)
plot(sig); title('Original Signal');
subplot(2,1,2)
plot(a3); title('Level-3 Approximation Coefficients');

Figure contains 2 axes objects. Axes object 1 with title Original Signal contains an object of type line. Axes object 2 with title Level-3 Approximation Coefficients contains an object of type line.

You can substitute any value from 1 to 5 for Lev to obtain the approximation coefficients for the corresponding level.

Input Arguments

collapse all

Wavelet decomposition vector of a 1-D signal, specified as a real-valued vector. C is the output of wavedec. The bookkeeping vector L is used to parse the coefficients in the wavelet decomposition vector by level.

Example: [C,L] = wavedec(randn(1,256),4,'coif1') returns the 4-level wavelet decomposition of a vector.

Data Types: single | double
Complex Number Support: Yes

Bookkeeping vector of the wavelet decomposition of a 1-D signal, specified as a vector of positive integers. The bookkeeping vector is used to parse the coefficients in the wavelet decomposition vector C by level.

Example: [C,L] = wavedec(randn(1,256),4,'coif1') returns the 4-level wavelet decomposition of a vector.

Data Types: single | double

Wavelet used to generate the wavelet decomposition of a 1-D signal, specified as a character vector or string scalar. The wavelet is from one of the following wavelet families: Best-localized Daubechies, Beylkin, Coiflets, Daubechies, Fejér-Korovkin, Haar, Han linear-phase moments, Morris minimum-bandwidth, Symlets, Vaidyanathan, Discrete Meyer, Biorthogonal, and Reverse Biorthogonal. See wavemngr for the wavelets available in each family.

Example: 'db4'

Wavelet lowpass reconstruction filter, specified as an even-length real-valued vector. LoR must be the same length as HiR. LoR must be the lowpass reconstruction filter associated with the wavelet used to create the wavelet decomposition structure [C,L]. (See wfilters for more information.)

Wavelet highpass reconstruction filter, specified as an even-length real-valued vector. HiR must be the same length as LoR. HiR must be the highpass reconstruction filter associated with the wavelet used to create the wavelet decomposition structure [C,L]. (See wfilters for more information.)

Approximation coefficients level, specified as a positive integer. If [C,L] is the M-level wavelet decomposition structure of a 1-D signal, then 0 ≤ N ≤ M.

Output Arguments

collapse all

Approximation coefficients at level N, returned as a real-valued vector.

Algorithms

The input vectors C and L contain all the information about the signal decomposition.

Let NMAX = length(L)-2; then C = [A(NMAX) D(NMAX) ... D(1)] where A and the D are vectors. If N = NMAX, then a simple extraction is done; otherwise, appcoef computes iteratively the approximation coefficients using the inverse wavelet transform.

Extended Capabilities

Version History

Introduced before R2006a

See Also

|