ihaart

Inverse 1-D Haar wavelet transform

Syntax

xrec = ihaart(a,d)

xrec = ihaart(a,d,level)

xrec = ihaart(___,integerflag)

Description

xrec = ihaart(a,d) returns the inverse 1-D Haar transform, xrec, for the approximation coefficients, a, and the wavelet coefficients, d. Both a and d are obtained from haart.

xrec = ihaart(a,d,level) returns the inverse 1-D Haar transform at the specified level.

xrec = ihaart(___,integerflag) specifies how the inverse 1-D Haar transform handles integer-valued data, using any of the previous syntaxes.

Examples

Inverse Haar Transform of Noisy Data

Obtain the Haar and inverse Haar transforms of noisy data.

Load the noisy data signal

 load noisdopp;

Obtain the Haar transform of the noisy signal.

 [a,d] = haart(noisdopp);

Reconstruct the data by inverting the Haar transform.

 xrec = ihaart(a,d);

Compare the original and reconstructed data by determining the maximum difference between them. The difference is essentially zero, which indicates a near-perfect reconstruction.

 max(abs(xrec-noisdopp'))

ans = 
4.4409e-15

Inverse Haar Transform of ECG Data

Obtain the Haar transform and inverse Haar transform of ECG heart rate data.

Load and plot the ECG data.

load BabyECGData;
plot(times,HR)
xlabel('Hours')
ylabel('Heart Rate')
title('ECG Data')

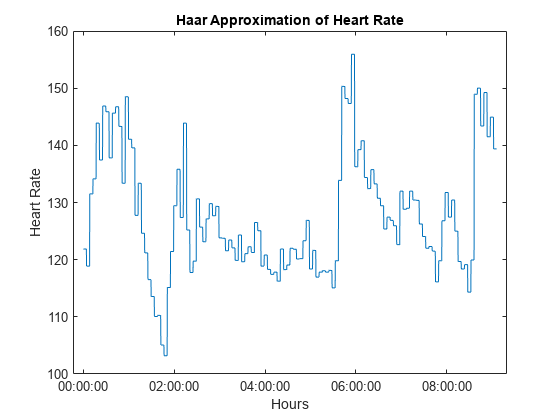
Obtain the Haar transform and inverse Haar transform. Compare the reconstructed data at level 4 to the original data.

[a,d] = haart(HR);
HaarHR = ihaart(a,d,4);
figure
plot(times,HaarHR)
xlabel('Hours')
ylabel('Heart Rate')
title('Haar Approximation of Heart Rate')

Inverse Haar Transform of Integer Data

Obtain the Haar and inverse Haar transforms for a series of random integers.

Create the series.

x = randi(10,100,1);

Obtain the Haar and inverse Haar transforms.

[a,d] = haart(x,'integer');
xrec = ihaart(a,d,'integer');

Plot and compare the original and reconstructed data.

subplot(2,1,1)
stem(x); title('Original Data')
subplot(2,1,2)
stem(xrec)
title('Reconstructed Integer-to-Integer Data')

Determine the maximum difference between the original data values and the reconstructed values. The difference is zero, which indicates perfect reconstruction.

max(abs(x(:)-xrec(:)))

ans = 
0

Input Arguments

a — Approximation coefficients

scalar | vector | matrix

Approximation coefficients, specified as a scalar, vector, or matrix of coefficients, depending on the level to which the Haar transform was calculated. a is an output from the haart function.

Approximation, or scaling, coefficients are a lowpass representation of the input. At each level the approximation coefficients are divided into coarser approximation and detail coefficients.

Data Types: single | double
Complex Number Support: Yes

d — Detail coefficients

scalar | vector | matrix | cell array

Detail coefficients, specified as a scalar, vector, matrix, or cell array of wavelet coefficients. d is an output from the haart function. The number of detail coefficients depends on the selected level and the length of the input. If d is a cell array, the elements of d are ordered from finest to coarsest resolution.

If d is a cell array, it can contain scalars, vectors, or matrices. The level of the Haar transform equals the number of elements in d.

If d is a vector or matrix, the Haar transform was computed only down to one level coarser in resolution.

If a and the elements of d are vectors, xrec is a vector. If a and the elements of d are matrices, xrec is a matrix, where each column is the inverse Haar transform of the corresponding columns in a and d.

Data Types: single | double
Complex Number Support: Yes

level — Maximum level

0 (default) | nonnegative integer

Maximum level to which to invert the Haar transform, specified as a nonnegative integer. If d is a cell array, level is less than or equal to length(d)-1. If d is a vector or matrix, level must equal 0 or be unspecified. The level must be less than the level used to obtain a and d from haart.

integerflag — Integer-valued data handling

'noninteger' (default) | 'integer'

Integer-valued data handling, specified as either 'noninteger' or 'integer'. 'noninteger' does not preserve integer-valued data, and 'integer' preserves it. The 'integer' option applies only if all elements of a and d are integer-valued. You must have used 'integer' with haart to obtain integer-valued a and d inputs. The inverse 1-D Haar transform algorithm, however, uses floating-point arithmetic.

Output Arguments

xrec — Inverse 1-D Haar wavelet transform

vector | matrix

Inverse 1-D Haar wavelet transform, returned as a vector or matrix. If a and the elements of d are vectors, xrec is a vector. If a and the elements of d are matrices, xrec is a matrix, where each column is the inverse 1-D Haar transform of the corresponding columns in a and d.

Data Types: single | double

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

Introduced in R2016b