Damping and frequency from simulation data
14 vues (au cours des 30 derniers jours)
Afficher commentaires plus anciens
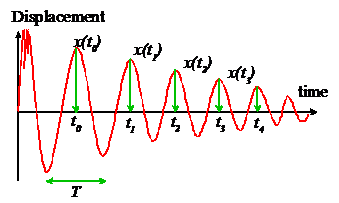
I have some simulation data, for example y in the attachment. I can manually calculate the damping and frequency with logarithmic decrement, but can I do this automated? I can't seem to figure out how.
And/or can I fit a nonlinear function through my datapoints? I tried polyfit but that doesn't work with time series.
2 commentaires
Ameer Hamza
le 2 Avr 2020
How do you manually calculate the damping and frequency? Is there a mathematical formula? What type of nonlinear fit do you want to fit your data?
Réponses (1)
Ameer Hamza
le 3 Avr 2020
The following code automatically estimate the parameters from the signal.
load('PositionY_example.mat');
[val, locs] = findpeaks(y.Data);
peak_times = y.Time(locs);
t0 = t(locs(1));
tn = t(locs(2:end));
omega = mean((1:numel(tn))'./(tn-t0));
xt0 = val(1);
xtn = val(2:end);
delta = mean(log(xtn./xt0)./(1:numel(xtn))');
zeta = delta/sqrt(4*pi^2+delta^2);
As you already know the value of ω, δ, and ζ of your signal, you can calculate the nonlinear fit for your data using this equation.
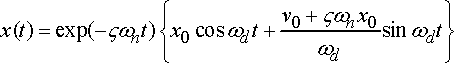
2 commentaires
MD Riaz Pervez
le 28 Avr 2023
t represent time. Here use t=Time therefore change that to make a single
Voir également
Catégories
En savoir plus sur Nonlinear Control dans Help Center et File Exchange
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!