FindRoots
FindRoots estimates the real roots (zeros) of a real (oscillatory) function FUN on the interval [A,B], by using adaptive nth-order (n=2^k) Chebyshev polynomial approximation of the function FUN.
This code was adapted from the code published in Day & Romero (2005): Roots Of Polynomials Expressed In Terms Of Orthogonal Polynomials. SIAM Journal on Numerical Analysis, 43, 1969-1987.
SYNTAX:
roots = FindRoots(fun,A,B)
roots = FindRoots(fun,A,B,n,isplot)
INPUTS:
fun - function handle, e.g. fun = @(x)sin(x).
A,B - lower and upper limit of the interval [A,B]. Default values are: A = -1, and B = 1.
n - polynomial order for approximation of the function fun, on each (automatically selected) sub-interval of [A,B]. n should be power of 2. Default value is n = 2^5. Increase the value of n if FindRoots is unable to find all roots of fun over the interval [A,B].
isplot - logical flag. If isplot = true, FindRoots plots the graph of the function together with depicted locations of its roots.
EXAMPLE 1:
fun = @(t) sin(t.^3 + t.^2 + t)
A = 0;
B = 5;
roots = FindRoots(fun,A,B)
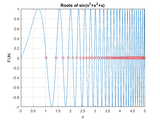
EXAMPLE 2:
fun = @(t) exp(-.3*t) .* sin(10*t) .* cos(2*t.^2)
A = 5;
B = 15;
roots = FindRoots(fun,A,B)
EXAMPLE 3:
x = 3;
nu = 1;
cf_chi2 = @(t) (1 - 2i * t) .^(-nu/2);
fun = @(t) min(4,imag(exp(-1i*t*x).*cf_chi2(t))./t)
A = 0.2;
B = 10;
n = 2^7;
roots = FindRoots(fun,A,B,n)
EXAMPLE 4:
nu = 3;
fun = @(t) sin(0.5+5*t) .* (besselj(nu,t) - besselk(nu,t))
A = 150;
B = 200;
roots = FindRoots(fun,A,B)
Acknowledgements: Chebfun inspired this file. For more details see http://www.chebfun.org/.
Citation pour cette source
Viktor Witkovsky (2026). FindRoots (https://fr.mathworks.com/matlabcentral/fileexchange/55206-findroots), MATLAB Central File Exchange. Extrait(e) le .
Compatibilité avec les versions de MATLAB
Plateformes compatibles
Windows macOS LinuxCatégories
- MATLAB > Mathematics > Elementary Math > Polynomials >
Tags
Remerciements
Inspiré par : Chebfun - current version
Découvrir Live Editor
Créez des scripts avec du code, des résultats et du texte formaté dans un même document exécutable.
| Version | Publié le | Notes de version | |
|---|---|---|---|
| 1.0.0.0 | Added more detailed description of the input parameters. |