Modélisation de systèmes de contrôle avec des objets de modèle
Les objets de modèle peuvent représenter les différentes composants d’une architecture de contrôle, comme le système physique, des actionneurs, des capteurs ou des contrôleurs. Vous pouvez connecter des objets de modèle afin de construire des modèles agrégés de schémas blocs représentant la réponse combinée de plusieurs éléments.
Par exemple, le système de contrôle suivant contient un préfiltre F, un système physique G et un contrôleur C, agencés au sein d’une configuration en boucle unique. Le modèle comprend également une représentation de la dynamique des capteurs, S.
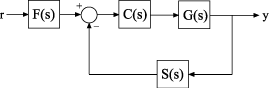
Vous pouvez représenter chaque composant sous la forme d’un objet de modèle. Il n'est pas nécessaire d’utiliser le même type d’objet de modèle pour chaque composant. Par exemple, représentez le système physique G en tant que modèle zéro-pôle-gain (zpk) avec un double pôle à s = -1 ; C en tant que contrôleur, PID et F et S en tant que fonctions de transfert :
G = zpk([],[-1,-1],1); C = pid(2,1.3,0.3,0.5); S = tf(5,[1 4]); F = tf(1,[1 1]);
Vous pouvez alors combiner ces éléments afin de construire des modèles représentant votre système de contrôle ou le système de contrôle dans son ensemble. Par exemple, créez la réponse en boucle ouverte SGC :
open_loop = S*G*C;
Pour construire un modèle de réponse en boucle fermée non filtrée, utilisez la commande feedback :
T = feedback(G*C,S);
Pour modéliser l’ensemble de la réponse du système en boucle fermée de r à y, combinez T avec la fonction de transfert de filtre :
Try = T*F;
Les résultats open_loop, T et Try sont également des objets de modèle linéaire. Vous pouvez agir dessus avec les commandes de design de contrôle et d'analyse de Control System Toolbox™. Par exemple, tracez la réponse indicielle de l’ensemble du système :
stepplot(Try)
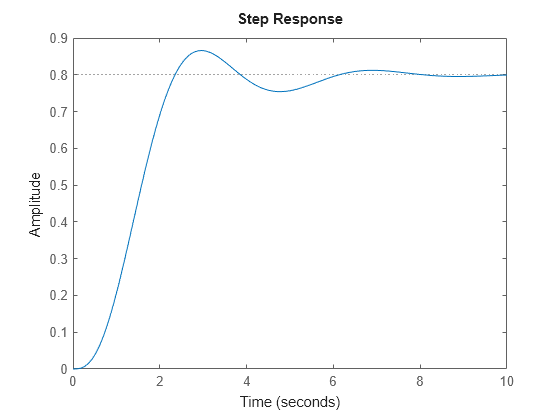
Lorsque vous combinez des modèles LTI numériques, le modèle obtenu représente le système agrégé. Le modèle obtenu ne conserve pas les données d’origine issus des composants assemblés. Par exemple, T n'assure pas le suivi distinct de la dynamique des composants G, C, et S qui sont combinés pour créer T.