FIR Halfband Filter Design
This example shows how to design FIR halfband filters. Halfband filters are widely used in multirate signal processing applications when you interpolate or decimate by a factor of two. In many cases, you can implement halfband filters efficiently in a polyphase form because nearly half of the halfband filter coefficients are equal to zero.
Halfband filters have two important characteristics:
The passband and stopband ripples must be the same.
The passband- and stopband-edge frequencies are equidistant from the halfband frequency Hz or rad/sample in normalized frequency.
Design a Halfband Filter using the designHalfbandFIR function
Use the designHalfbandFIR function to design an FIR halfband filter. The function returns the filter coefficients or one of the supported FIR filter objects.
Design an Equiripple Halfband Filter
Consider a halfband filter operating on data sampled at 96 kHz with a passband frequency edge of 22 kHz. The halfband frequency corresponding to that sample rate is 24 kHz, which amounts to a quarter of the sample rate. The transition width of that design is 2kHz, or 1/12 rad/sec in normalized units. Set DesignMethod to "equiripple".
Fs = 96e3; % Sample rate Fp = 22e3; % Passband edge Fh = Fs/4; % Halfband frequency TW = (Fh-Fp)/Fh; % Normalized transition width N = 100; % Filter order num = designHalfbandFIR(FilterOrder=N,TransitionWidth=TW,Passband="lowpass",DesignMethod="equiripple"); zerophase(num,1,linspace(0,Fs/2,512),Fs);
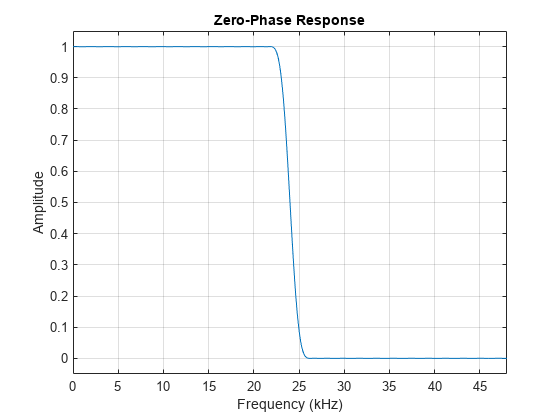
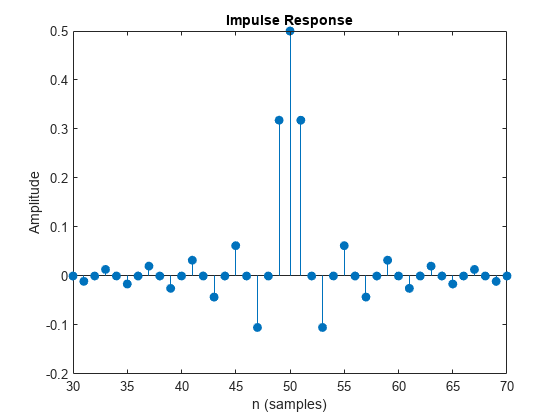
By zooming in on the response, you can verify that the passband and stopband peak-to-peak ripples are the same. There is symmetry about the (24 kHz) point. The passband extends up to 22 kHz as specified and the stopband begins at 26 kHz. You can also verify that every other coefficient is equal to zero by looking at the impulse response. This makes the filter very efficient to implement for interpolation or decimation by a factor of 2.
impz(num); xlim([30 70])
Filtering Streaming Data Through a Halfband Filter
When working with streaming data, use the dsp.FIRFilter, dsp.FIRHalfbandInterpolator and dsp.FIRHalfbandDecimator System objects, which provide efficient filter implementations. These System objects support filtering double and single precision floating-point data as well as fixed-point data. They also support C and HDL code generation as well as optimized ARM® Cortex® M and ARM® Cortex® A code generation. When using dsp.FIRFilter, use designHalfbandFIR with Structure set to 'single-rate'. When using dsp.FIRHalfbandInterpolator and dsp.FIRHalfbandDecimator, set Structure to 'interp' or 'decim' respectively.
Construct an FIR halfband single-rate filter.
num = designHalfbandFIR(FilterOrder=N,TransitionWidth=TW,Passband="lowpass",DesignMethod="equiripple",Structure="single-rate"); halfbandFilter = dsp.FIRFilter(num)
halfbandFilter =
dsp.FIRFilter with properties:
Structure: 'Direct form'
NumeratorSource: 'Property'
Numerator: [0 2.1118e-04 0 -2.4012e-04 0 3.7199e-04 0 -5.4746e-04 0 7.7546e-04 0 -0.0011 0 0.0014 0 -0.0019 0 0.0024 0 -0.0031 0 0.0039 0 -0.0049 0 0.0060 0 -0.0074 0 0.0090 0 -0.0110 0 0.0134 0 -0.0163 0 0.0201 0 -0.0252 0 … ] (1×101 double)
InitialConditions: 0
Show all properties
You can create a System object directly through designHalfbandFIR by setting SystemObject parameter to true.
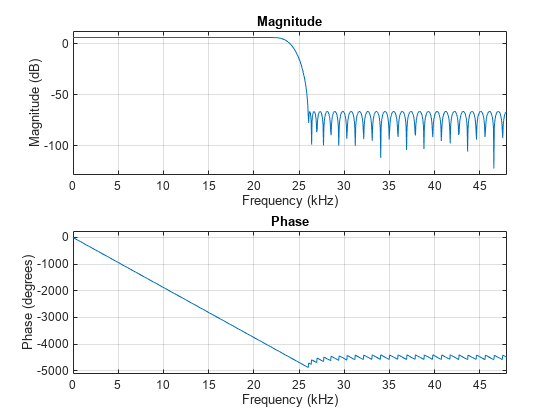
Construct an FIR halfband interpolator.
halfbandInterpolator = designHalfbandFIR(FilterOrder=N, TransitionWidth=TW,... Passband="lowpass",DesignMethod="equiripple",... Structure="interp",SystemObject=true); freqz(halfbandInterpolator,1024,Fs);
Self-Design Mode of dsp.FIRHalfbandInterpolator and dsp.FIRHalfbandDecimator
The dsp.FIRHalfbandInterpolator and dsp.FIRHalfbandDecimator System objects can internally design the filter coefficients. To use that option, construct a dsp.FIRHalfbandInterpolator or a dsp.FIRHalfbandDecimator System object, and specify which design specification is used through the Specification property. The object is self-designing when Specification is not set to 'Coefficients'. The objects use the same parameter names as the designHalfbandFIR function: FilterOrder, TransitionWidth, and StopbandAttenuation. Another advantage of using self-designing mode the support for arbitrary sample rates in addition to normalize frequency units.
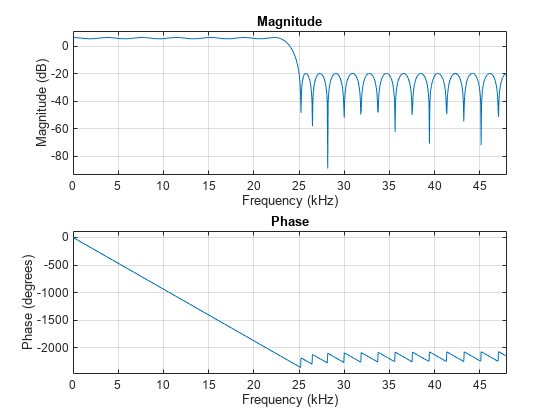
Construct a halfband interpolator at a sample rate of 96 kHz, with filter order of 50, and a transition width of 4 kHz.
Fs = 96e3; % Sample rate TW = 4e3; % Transition width N = 50; % Filter order halfbandInterpolator = dsp.FIRHalfbandInterpolator(SampleRate=Fs,... Specification="Filter order and transition width",... FilterOrder=N,TransitionWidth=TW); freqz(halfbandInterpolator,1024,Fs);
As long as the object is not locked, you can tune the design parameters, and the design changes accordingly.
halfbandInterpolator.FilterOrder=N*2; freqz(halfbandInterpolator,1024,Fs);
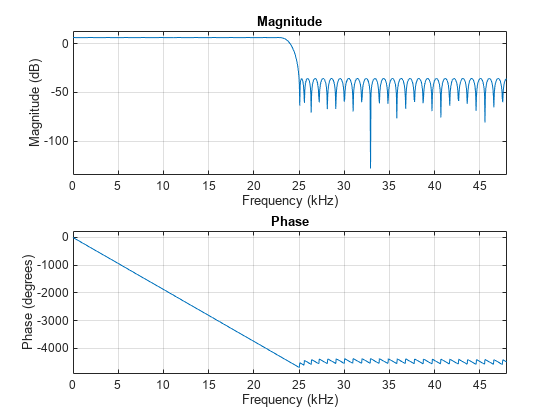
Use the tf function to extract the coefficients of the FIR halfband interpolator or decimator System object. The filter order in the example above is 100, as expected.
num = tf(halfbandInterpolator); length(num)
ans = 101
To perform the halfband interpolation, pass the input data through the dsp.FIRHalfbandInterpolator System object.
FrameSize = 256; sine1 = dsp.SineWave(Frequency=10e3,SampleRate=Fs,SamplesPerFrame=FrameSize); sine2 = dsp.SineWave(Frequency=20e3,SampleRate=Fs,SamplesPerFrame=FrameSize); x = sine1() + sine2() + 0.01.*randn(FrameSize,1); % Input signal y = halfbandInterpolator(x); % Step through the object
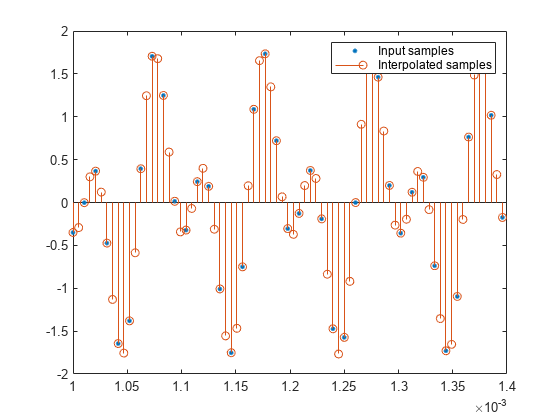
Plot the interpolated samples overlaid on the input samples by compensating for the delay of the filter. Use the outputDelay function to obtain the filter delay. The input samples remain unchanged at the output of the filter because one of the polyphase branches of the halfband filter is a pure delay branch that does not change the input samples.
[D, FsOut] = halfbandInterpolator.outputDelay(); nx = 0:length(x)-1; ny = 0:length(y)-1; plot(nx/Fs+D,x,".",MarkerSize=10) hold on stem(ny/FsOut,y) hold off legend("Input samples","Interpolated samples") xlim([1e-3, 1.4e-3])
Plot the spectral content of the output signal using spectrumAnalyzer. In the case of interpolation, you upsample by a factor of 2 and then filter (conceptually), therefore you need to specify the sample rate in spectrumAnalyzer as because of the upsampling by 2.
scope = spectrumAnalyzer(SampleRate=2*Fs); tic while toc < 10 x = sine1() + sine2() + 0.01.*randn(FrameSize,1); % 96 kHz y = halfbandInterpolator(x); % 192 kHz scope(y); end release(scope);
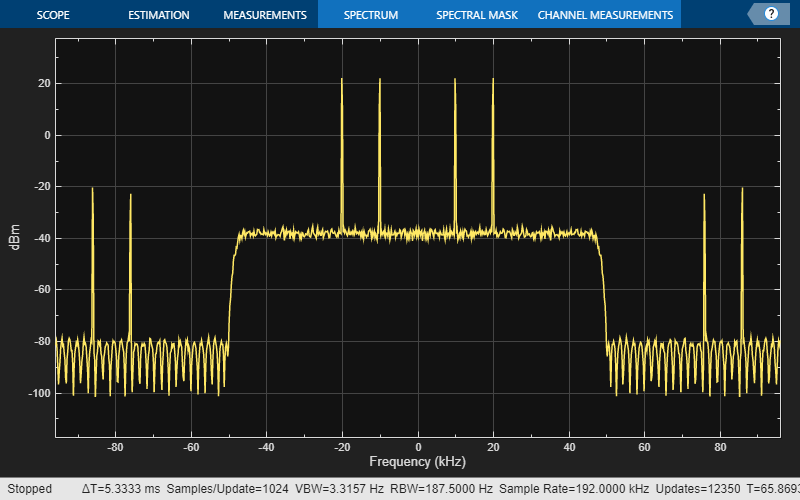
The spectral replicas are attenuated by about 40 dB, which is roughly the attenuation provided by the halfband filter.
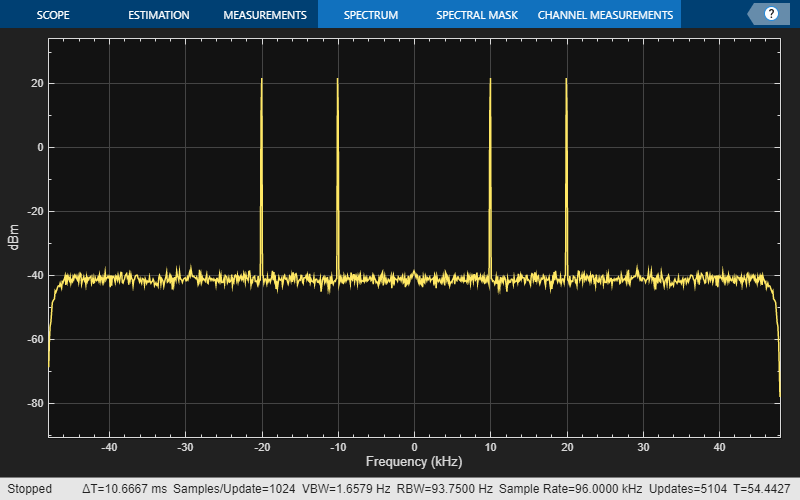
In the case of decimation, the sample rate you specify in the dsp.FIRHalfbandDecimator corresponds to the sample rate of the input, since the object filters and then downsamples (conceptually). Cascade a halfband decimator with the halfband interpolator that you designed in the previous section, and plot the spectral content of the output. The sample rate at the output of the two blocks is Fs, just like the input.
halfbandDecimator = dsp.FIRHalfbandDecimator(SampleRate=2*Fs,... Specification="Filter order and transition width",... FilterOrder=N,TransitionWidth=4000); scope = spectrumAnalyzer(SampleRate=Fs); tic while toc < 10 x = sine1() + sine2() + 0.01.*randn(FrameSize,1); % 96 kHz y = halfbandInterpolator(x); % 192 kHz xd = halfbandDecimator(y); % 96 kHz again scope(xd); end release(scope);
Minimum Order Design Specifications
Instead of specifying the filter order, you can specify a transition width and a stopband attenuation. The halfband filter design algorithm automatically attempts to find the smallest filter order which satisfies the specifications.
Ast = 80; % 80 dB num = designHalfbandFIR(StopbandAttenuation=Ast,TransitionWidth=4000/Fs,DesignMethod="equiripple"); minimumOrder = length(num)
minimumOrder = 223
freqz(num,1,1024,Fs)
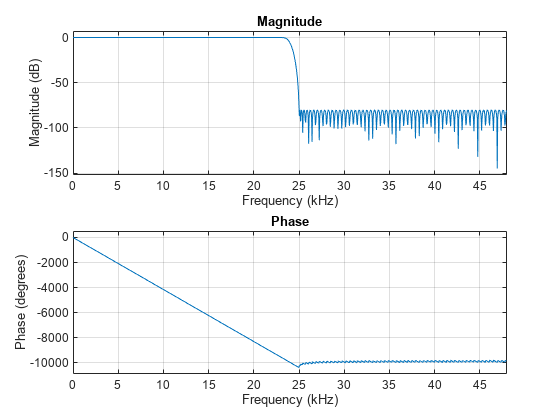
The same can be done with the dsp.FIRHalfbandInterpolator and the dsp.FIRHalfbandDecimator objects. However, you need to explicitly set the Specification property to "Transition width and stopband attenuation".
halfbandInterpolator = dsp.FIRHalfbandInterpolator(SampleRate=Fs,Specification="Transition width and stopband attenuation",... StopbandAttenuation=Ast, TransitionWidth=4000); freqz(halfbandInterpolator)
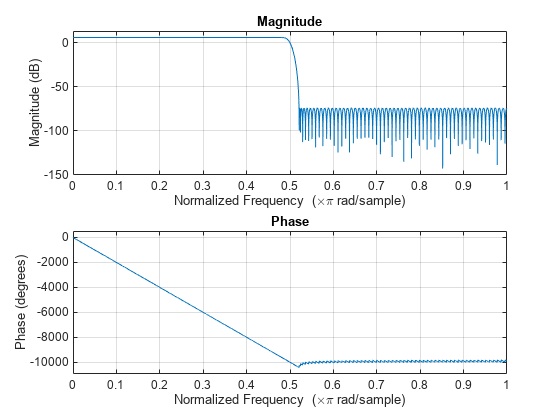
Specify Filter Order and Stopband Attenuation
You can also design the filter by specifying the filter order and the stopband attenuation.
num = designHalfbandFIR(StopbandAttenuation=Ast,FilterOrder=N,DesignMethod="equiripple");
freqz(num,1,1024,Fs);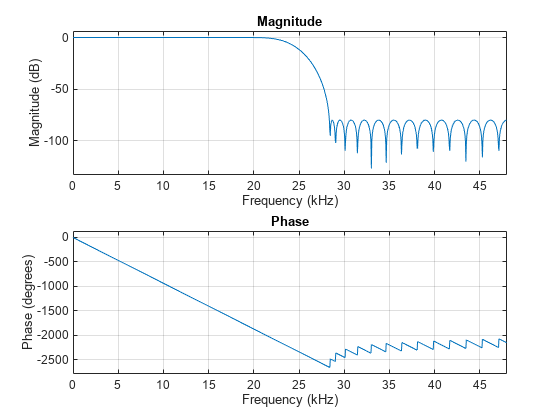
The same can be done with the dsp.FIRHalfbandInterpolator and the dsp.FIRHalfbandDecimator objects. However, you need to explicitly set the Specification property to "Filter order and stopband attenuation".
halfbandDecimator = dsp.FIRHalfbandDecimator(SampleRate=Fs,... Specification="Filter order and stopband attenuation",... StopbandAttenuation=Ast,FilterOrder=N); filterAnalyzer(halfbandDecimator);
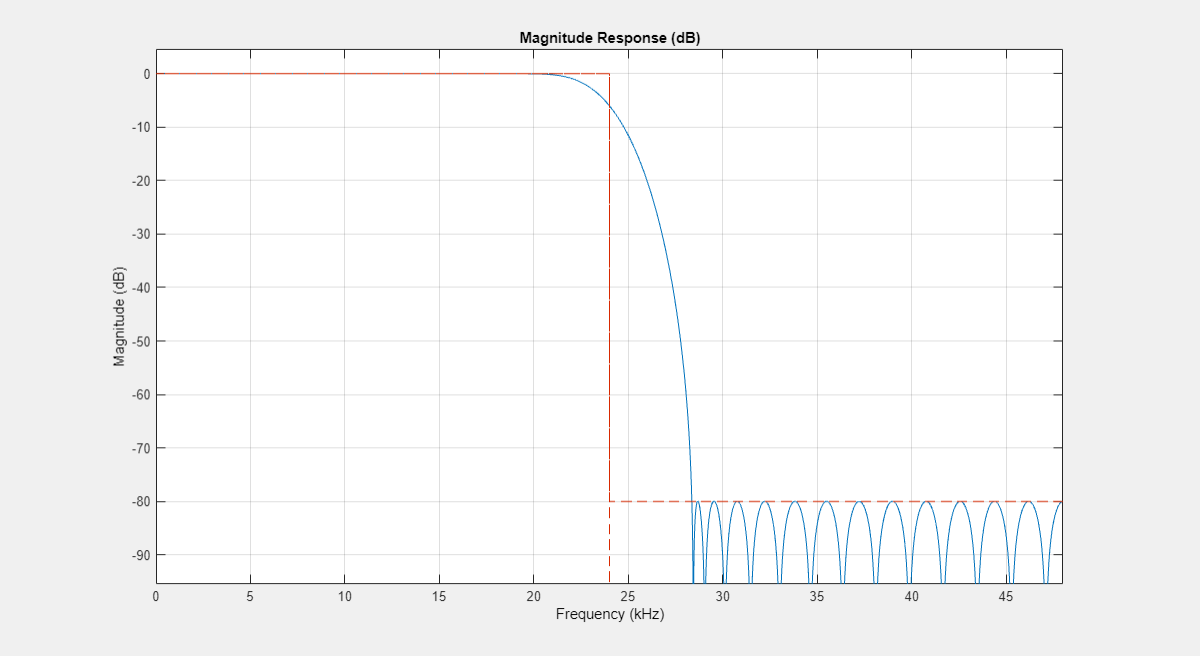
Use Halfband Filters for Filter Banks
You can use halfband interpolators and decimators to efficiently implement synthesis and analysis filter banks. The halfband filters discussed so far in the example were all lowpass filters. With a single extra adder, you can obtain a highpass response in addition to the lowpass response and use the two responses to implement the filter bank.
Simulate a quadrature mirror filter (QMF) bank. First, separate an 8 kHz signal consisting of 1 kHz and 3 kHz sine waves into two half-rate signals (4 kHz) using a lowpass and highpass halfband decimator. The lowpass signal retains the 1 kHz sine wave while the highpass signal retains the 3 kHz sine wave (which is aliased to 1 kHz after downsampling). Merge the signals back together with a synthesis filter bank using a halfband interpolator. The highpass branch upconverts the aliased 1 kHz sine wave back to 3 kHz. The interpolated signal has an 8 kHz sample rate.
Fs1 = 8000; % Units = Hz Spec = "Filter order and transition width"; Order = 52; TW = 4.1e2; % Units = Hz % Construct FIR Halfband Interpolator halfbandInterpolator = dsp.FIRHalfbandInterpolator( ... Specification=Spec,... FilterOrder=Order,... TransitionWidth=TW,... SampleRate=Fs1/2,... FilterBankInputPort=true); % Construct FIR Halfband Decimator halfbandDecimator = dsp.FIRHalfbandDecimator( ... Specification=Spec,... FilterOrder=Order,... TransitionWidth=TW,... SampleRate=Fs1); % Input f1 = 1000; f2 = 3000; InputWave = dsp.SineWave(Frequency=[f1,f2],SampleRate=Fs1,... SamplesPerFrame=1024,Amplitude=[1 0.25]); % Construct Spectrum Analyzer object to view the input and output scope = spectrumAnalyzer(SampleRate=Fs1,... PlotAsTwoSidedSpectrum=false,ShowLegend=true,... YLimits=[-120 30],... Title="Input Signal and Output Signal of Quadrature Mirror Filter",... ChannelNames={"Input","Output"}); tic while toc < 10 Input = sum(InputWave(),2); NoisyInput = Input+(10^-5)*randn(1024,1); [Lowpass,Highpass] = halfbandDecimator(NoisyInput); Output = halfbandInterpolator(Lowpass,Highpass); scope([NoisyInput,Output]); end release(scope);

Kaiser Window Designs
All designs presented so far in the example were optimal equiripple designs. The designHalfbandFIR function, as well as the dsp.FIRHalfbandDecimator and dsp.FIRHalfbandInterpolator System objects can also design halfband filters using the Kaiser window method.
Compare an equiripple and Kaiser window filter designs. Use the same specifications sample rate, filter order, and transition bandwidth that were used in the previous steps.
Fs = 44.1e3; N = 90; TW = 1000; equirippleHBFilter = designHalfbandFIR(DesignMethod="equiripple",... TransitionWidth=TW/Fs,FilterOrder=N); kaiserHBFilter = designHalfbandFIR(DesignMethod="kaiser",... TransitionWidth=TW/Fs,FilterOrder=N);
Compare the designs using filterAnalyzer. The two designs allow for tradeoffs between minimum stopband attenuation and larger overall attenuation.
FA = filterAnalyzer({equirippleHBFilter,1,1},{kaiserHBFilter,1,1},SampleRates=2*Fs);
setLegendStrings(FA,["Equiripple design","Kaiser-window design"])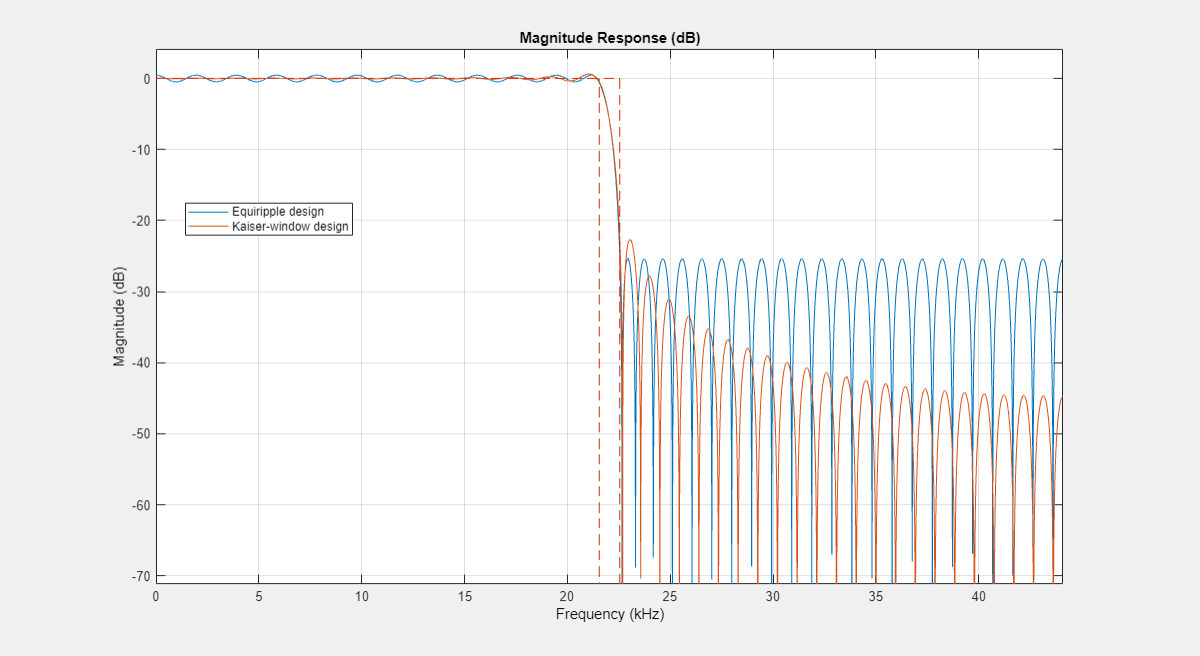
Specify the Stopband Attenuation in Kaiser Design
Alternatively, one can specify the order and the stopband attenuation. This allows for tradeoffs between overall stopband attenuation and transition width.
Ast = 60; % Minimum stopband attenuation equirippleHBFilter = designHalfbandFIR(DesignMethod="equiripple",... StopbandAttenuation=Ast,FilterOrder=N); kaiserHBFilter = designHalfbandFIR(DesignMethod="kaiser",... StopbandAttenuation=Ast,FilterOrder=N); FA = filterAnalyzer({equirippleHBFilter,1,1},{kaiserHBFilter,1,1},SampleRates=2*Fs); setLegendStrings(FA,["Equiripple design","Kaiser-window design"])
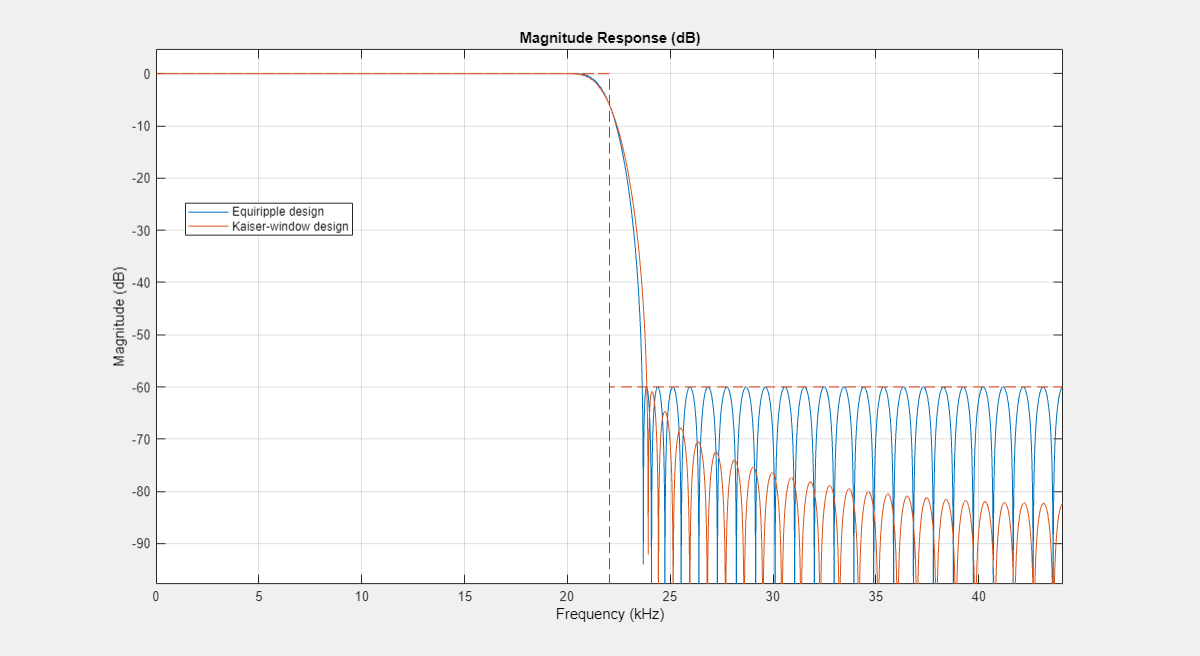
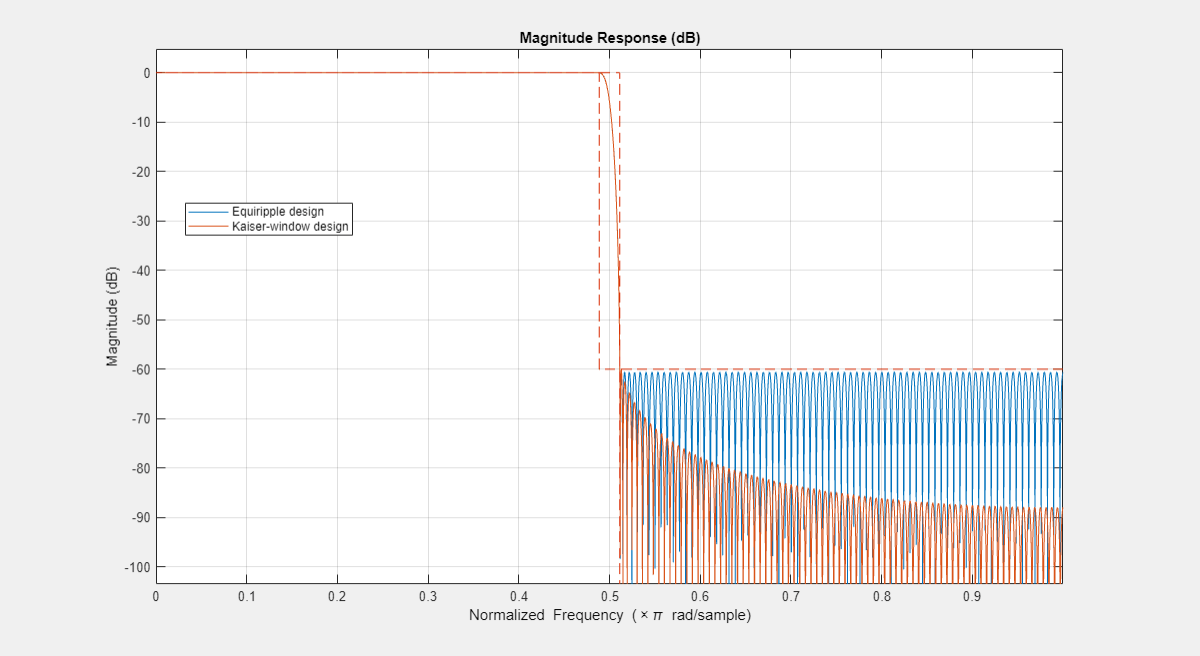
Minimum-Order Kaiser Designs
The Kaiser window design method also supports minimum order designs. Specify a target transition width and a stopband attenuation, and the design algorithm attempts to find the smaller order Kaiser FIR halfband that satisfies the target specifications. A minimum-order Kaiser design usually has a larger order than its equiripple counterpart, but the overall stopband attenuation is better in return.
Fs = 44.1e3; TW = 1000; % Transition width Ast = 60; % 60 dB minimum attenuation in the stopband equirippleHBFilter = designHalfbandFIR(DesignMethod="equiripple",... StopbandAttenuation=Ast,TransitionWidth=TW/Fs); kaiserHBFilter = designHalfbandFIR(DesignMethod="kaiser",... StopbandAttenuation=Ast,TransitionWidth=TW/Fs); FA = filterAnalyzer({equirippleHBFilter,1,1},{kaiserHBFilter,1,1}, SampleRates=Fs); setLegendStrings(FA,["Equiripple design","Kaiser-window design"])
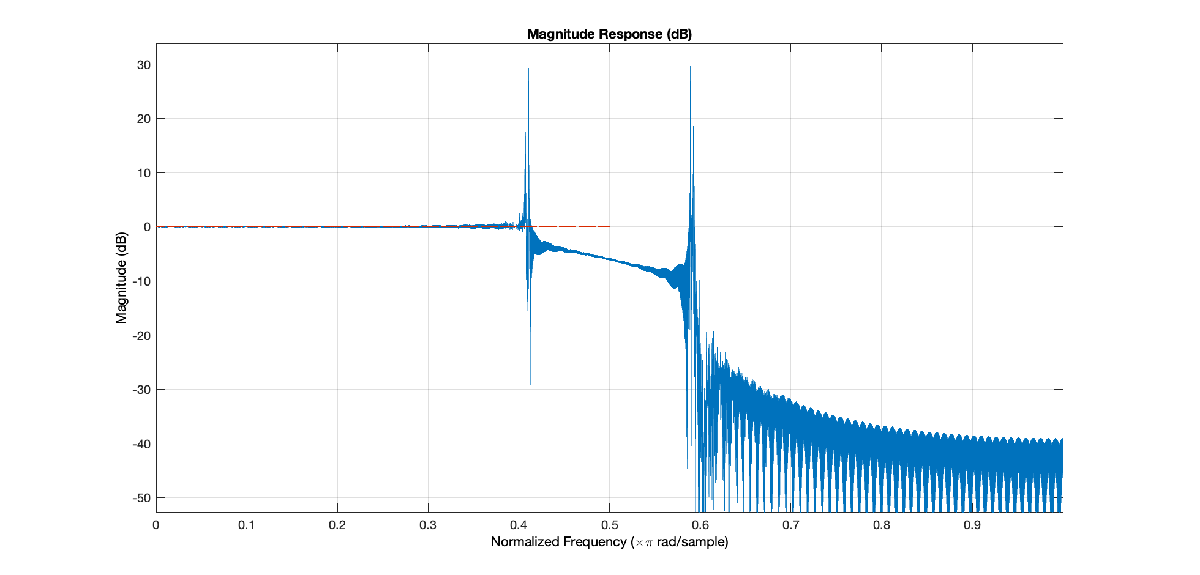
Automatically Set Filter Design Method
The Kaiser method and Equiripple method have different strengths depending on the design specifications. For tight design specifications such as very high stopband attenuation or a very narrow transition width, the Equiripple design method often fails to converge. In such cases, the Kaiser method is superior.
This code illustrates a case where the filter specifications are too tight to use an equiripple design. Set the DesignMethod property to "Equiripple", and the design fails to converge as you can observe from the frequency response of the filter.
TW = 0.001; Ast = 180; % 180 dB minimum attenuation in the stopband equirippleHBFilter = designHalfbandFIR(DesignMethod="equiripple",... TransitionWidth=TW,... StopbandAttenuation=Ast,... SystemObject=true); FA = filterAnalyzer(equirippleHBFilter); setLegendStrings(FA,"DesignMethod = equiripple");
Repeat the design with DesignMethod set to "kaiser". While the kaiser-based filter design does not accurately meet the tight design specifications, the filter better converges as you can see by comparing the frequency response of the two filters.
kaiserHBFilter = designHalfbandFIR(DesignMethod="kaiser",... TransitionWidth=TW,... StopbandAttenuation=Ast,... SystemObject=true); FA = filterAnalyzer(kaiserHBFilter); setLegendStrings(FA,"DesignMethod = kaiser");
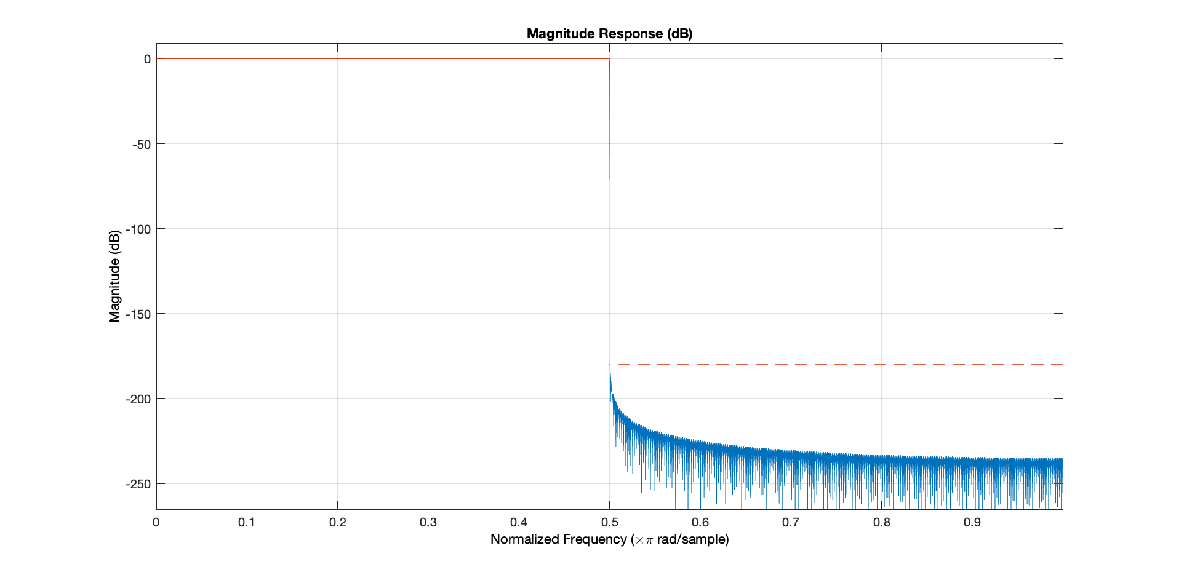
In addition to "equiripple" and "kaiser", you can set DesignMethod to "Auto". When you set the DesignMethod to "Auto", the designHalfbandFIR function selects the design method automatically based on the filter design parameters. This is the default design method used when you don't specify the DesignMethod parameter. You can determine which design method is selected by passing the Verbose=true argument. In the code below, the function automatically selects an Equiripple design.
TW = 1/44.1; Ast = 180; autoHBFilter = designHalfbandFIR(DesignMethod="auto",... TransitionWidth=TW,... StopbandAttenuation=Ast, ... Verbose=true);
designHalfbandFIR(TransitionWidth=0.022675736961451247, StopbandAttenuation=180, DesignMethod="kaiser", Passband="lowpass", Structure="single-rate", InputSampleRate="normalized", PhaseConstraint="linear", Datatype="double", SystemObject=false)
FA = filterAnalyzer(autoHBFilter);
setLegendStrings(FA,"designHalfbandFIR, DesignMethod = auto");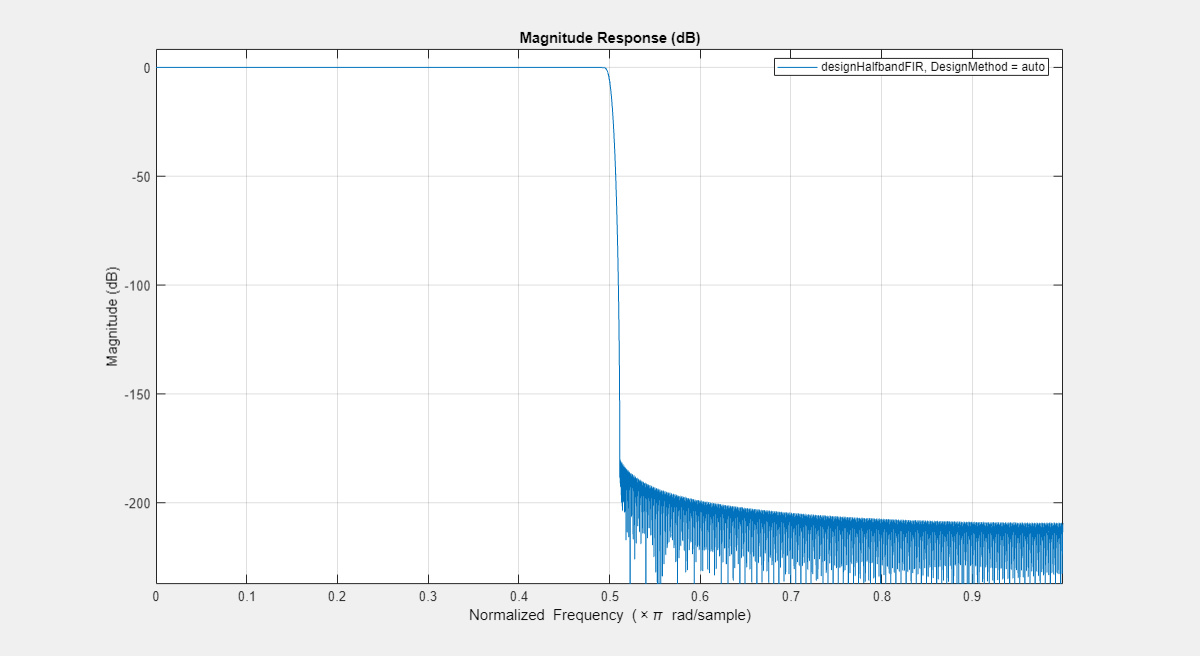
The dsp.FIRHalfbandDecimator and dsp.FIRHalfbandInterpolator System objects also support the "auto" design method.
Fs = 44.1e3; TW = 1000; % Transition width Ast = 60; % 60 dB minimum attenuation in the stopband autoHBFilter = dsp.FIRHalfbandDecimator(Specification="Transition width and stopband attenuation",... SampleRate=Fs,... TransitionWidth=TW,... StopbandAttenuation=Ast, ... DesignMethod="auto"); FA = filterAnalyzer(autoHBFilter); setLegendStrings(FA,"dsp.FIRHalfbandDecimator, DesignMethod = auto");
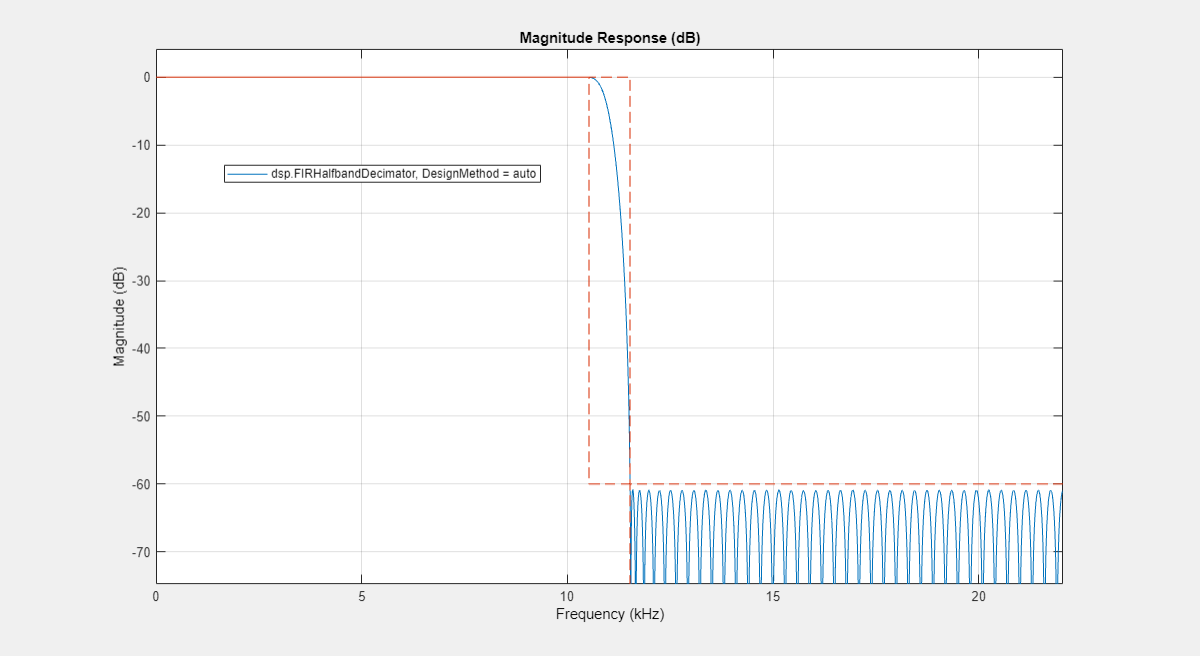
If the design constraints are very tight, then the design algorithm automatically selects the Kaiser window method, as this method proves to be optimal choice when designing filters with very tight specifications. However, if the design constraints are not tight, then the algorithm selects the equiripple design method.