simulate
Syntax
Description
[
returns 1000 random vectors of state-space model parameters Params,accept] = simulate(PriorMdl,Y,params0,Proposal)Params drawn
from the posterior distribution
Π(θ|Y), where
PriorMdl specifies the prior distribution and data likelihood, and
Y is the observed response data. params0 is the
set of initial parameter values and Proposal is the covariance matrix
of the proposal distribution of the Metropolis-Hastings (MH) sampler [1][2]. accept is the
acceptance rate of the proposal draws.
[
specifies options using one or more name-value arguments. For example,
Params,accept] = simulate(PriorMdl,Y,params0,Proposal,Name=Value)simulate(PriorMdl,Y,params0,Proposal,NumDraws=1e6,Thin=3,DoF=10) uses
the multivariate t10 distribution for the
Metropolis-Hastings proposal, draws 3e6 random vectors of parameters, and
thins the sample to reduce serial correlation by discarding every 2 draws until it retains
1e6 draws.
[
also returns the output Params,accept,Output] = simulate(PriorMdl,Y,params0,Proposal,Name=Value)Output of the custom function that monitors the
Markov-chain Monte Carlo (MCMC) algorithm at each iteration, specified by the
OutputFunction name-value argument.
Examples
Simulate observed responses from a known state-space model, then treat the model as Bayesian and draw parameters from the posterior distribution.
Suppose the following state-space model is a data-generating process (DGP).
Create a standard state-space model object ssm that represents the DGP.
trueTheta = [0.5; -0.75; 1; 0.5]; A = [trueTheta(1) 0; 0 trueTheta(2)]; B = [trueTheta(3) 0; 0 trueTheta(4)]; C = [1 1]; DGP = ssm(A,B,C);
Simulate a response path from the DGP.
rng(1); % For reproducibility
y = simulate(DGP,200);Suppose the structure of the DGP is known, but the state parameters trueTheta are unknown, explicitly
Consider a Bayesian state-space model representing the model with unknown parameters. Arbitrarily assume that the prior distribution of , , , and are independent Gaussian random variables with mean 0.5 and variance 1.
The Local Functions section contains two functions required to specify the Bayesian state-space model. You can use the functions only within this script.
The paramMap function accepts a vector of the unknown state-space model parameters and returns all the following quantities:
A= .B= .C= .D= 0.Mean0andCov0are empty arrays[], which specify the defaults.StateType= , indicating that each state is stationary.
The paramDistribution function accepts the same vector of unknown parameters as does paramMap, but it returns the log prior density of the parameters at their current values. Specify that parameter values outside the parameter space have log prior density of -Inf.
Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm.
Mdl = bssm(@paramMap,@priorDistribution)
Mdl =
Mapping that defines a state-space model:
@paramMap
Log density of parameter prior distribution:
@priorDistribution
The simulate function requires a proposal distribution scale matrix. You can obtain a data-driven proposal scale matrix by using the tune function. Alternatively, you can supply your own scale matrix.
Obtain a data-driven scale matrix by using the tune function. Supply a random set of initial parameter values, and shut off the estimation summary display.
numParams = 4; theta0 = rand(numParams,1); [theta0,Proposal] = tune(Mdl,y,theta0,Display=false);
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
Draw 1000 random parameter vectors from the posterior distribution. Specify the simulated response path as observed responses and the optimized values returned by tune for the initial parameter values and the proposal distribution.
[Theta,accept] = simulate(Mdl,y,theta0,Proposal); accept
accept = 0.4010
Theta is a 4-by-1000 matrix of randomly drawn parameters from the posterior distribution. Rows correspond to the elements of the input argument theta of the functions paramMap and priorDistribution.
accept is the proposal acceptance probability. In this case, simulate accepts 40% of the proposal draws.
Create trace plots of the parameters.
paramNames = ["\phi_1" "\phi_2" "\sigma_1" "\sigma_2"]; figure h = tiledlayout(4,1); for j = 1:numParams nexttile plot(Theta(j,:)) hold on yline(trueTheta(j)) ylabel(paramNames(j)) end title(h,"Posterior Trace Plots")
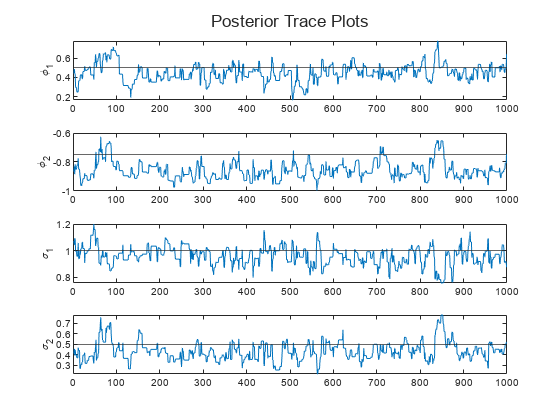
The sampler eventually settles at near the true values of the parameters. In this case, the sample shows serial correlation and transient behavior. You can remedy serial correlation in the sample by adjusting the Thin name-value argument, and you can remedy transient effects by increasing the burn-in period using the BurnIn name-value argument.
Local Functions
This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 1]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end
Consider the model in the example Draw Random Parameters from Posterior Distribution of Time-Invariant Model. Improve the Markov chain convergence by adjusting sampler options.
Create a standard state-space model object ssm that represents the DGP, and then simulate a response path.
trueTheta = [0.5; -0.75; 1; 0.5];
A = [trueTheta(1) 0; 0 trueTheta(2)];
B = [trueTheta(3) 0; 0 trueTheta(4)];
C = [1 1];
DGP = ssm(A,B,C);
rng(1); % For reproducibility
y = simulate(DGP,200);Create the Bayesian state-space model by passing function handles directly to paramMap and paramDistribution to bssm (the functions are in Local Functions).
Mdl = bssm(@paramMap,@priorDistribution)
Mdl =
Mapping that defines a state-space model:
@paramMap
Log density of parameter prior distribution:
@priorDistribution
Simulate random parameter vectors from the posterior distribution. Specify the simulated response path as observed responses, and obtain an optimal proposal distribution by using tune and shut off all optimization displays. The plots in Draw Random Parameters from Posterior Distribution of Time-Invariant Model suggest that the Markov chain settles after 500 draws. Therefore, specify a burn-in period of 500 (BurnIn=500). Specify thinning the sample by keeping the first draw of each set of 30 successive draws (Thin=30). Retain 2000 random parameter vectors (NumDraws=2000).
numParams = 4; theta0 = rand(numParams,1); options = optimoptions("fminunc",Display="off"); [theta0,Proposal] = tune(Mdl,y,theta0,Display=false,Options=options); [Theta,accept] = simulate(Mdl,y,theta0,Proposal, ... NumDraws=2000,BurnIn=500,Thin=30); accept
accept = 0.3885
Theta is a 4-by-2000 matrix of randomly drawn parameters from the posterior distribution. Rows correspond to the elements of the input argument theta of the functions paramMap and priorDistribution.
accept is the proposal acceptance probability. In this case, simulate accepts 39% of the proposal draws.
Create trace plots and correlograms of the parameters.
paramNames = ["\phi_1" "\phi_2" "\sigma_1" "\sigma_2"]; figure h = tiledlayout(4,1); for j = 1:numParams nexttile plot(Theta(j,:)) hold on yline(trueTheta(j)) ylabel(paramNames(j)) end title(h,"Posterior Trace Plots")

figure h = tiledlayout(4,1); for j = 1:numParams nexttile autocorr(Theta(j,:)); ylabel(paramNames(j)); title([]); end title(h,"Posterior Sample Correlograms")

The sampler quickly settles near the true values of the parameters. The sample shows little serial correlation and no transient behavior.
Local Functions
This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 1]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end
Consider the following time-varying, state-space model for a DGP:
From periods 1 through 250, the state equation includes stationary AR(2) and MA(1) models, respectively, and the observation model is the weighted sum of the two states.
From periods 251 through 500, the state model includes only the first AR(2) model.
and is the identity matrix.
Symbolically, the DGP is
where:
The AR(2) parameters and .
The MA(1) parameter .
The observation equation parameters and .
Write a function that specifies how the parameters theta and sample size T map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named timeVariantParamMapBayes.m on your MATLAB® path. Alternatively, open the example to access the function.
type timeVariantParamMapBayes.m% Copyright 2022 The MathWorks, Inc.
function [A,B,C,D,Mean0,Cov0,StateType] = timeVariantParamMapBayes(theta,T)
% Time-variant, Bayesian state-space model parameter mapping function
% example. This function maps the vector params to the state-space matrices
% (A, B, C, and D), the initial state value and the initial state variance
% (Mean0 and Cov0), and the type of state (StateType). From periods 1
% through T/2, the state model is a stationary AR(2) and an MA(1) model,
% and the observation model is the weighted sum of the two states. From
% periods T/2 + 1 through T, the state model is the AR(2) model only. The
% log prior distribution enforces parameter constraints (see
% flatPriorBSSM.m).
T1 = floor(T/2);
T2 = T - T1 - 1;
A1 = {[theta(1) theta(2) 0 0; 1 0 0 0; 0 0 0 theta(4); 0 0 0 0]};
B1 = {[theta(3) 0; 0 0; 0 1; 0 1]};
C1 = {theta(5)*[1 0 1 0]};
D1 = {theta(6)};
Mean0 = [0.5 0.5 0 0];
Cov0 = eye(4);
StateType = [0 0 0 0];
A2 = {[theta(1) theta(2) 0 0; 1 0 0 0]};
B2 = {[theta(3); 0]};
A3 = {[theta(1) theta(2); 1 0]};
B3 = {[theta(3); 0]};
C3 = {theta(7)*[1 0]};
D3 = {theta(8)};
A = [repmat(A1,T1,1); A2; repmat(A3,T2,1)];
B = [repmat(B1,T1,1); B2; repmat(B3,T2,1)];
C = [repmat(C1,T1,1); repmat(C3,T2+1,1)];
D = [repmat(D1,T1,1); repmat(D3,T2+1,1)];
end
Simulate a response path of length 500 from the model.
params = [0.5; -0.2; 0.4; 0.3; 2; 0.1; 3; 0.2]; numObs = 500; numParams = numel(params); [A,B,C,D,mean0,Cov0,stateType] = timeVariantParamMapBayes(params,numObs); DGP = ssm(A,B,C,D,Mean0=mean0,Cov0=Cov0,StateType=stateType); rng(1) % For reproducibility y = simulate(DGP,numObs); plot(y) ylabel("y")

Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorBSSM.m on your MATLAB® path. Alternatively, open the example to access the function.
type flatPriorBSSM.m% Copyright 2022 The MathWorks, Inc.
function logprior = flatPriorBSSM(theta)
% flatPriorBSSM computes the log of the flat prior density for the eight
% variables in theta (see timeVariantParamMapBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.
% theta(1) and theta(2) are lag 1 and lag 2 terms in a stationary AR(2)
% model. The eigenvalues of the AR(1) representation need to be within
% the unit circle.
evalsAR2 = eig([theta(1) theta(2); 1 0]);
evalsOutUC = sum(abs(evalsAR2) >= 1) > 0;
% Standard deviations of disturbances and errors (theta(3), theta(6),
% and theta(8)) need to be positive.
nonnegsig1 = theta(3) <= 0;
nonnegsig2 = theta(6) <= 0;
nonnegsig3 = theta(8) <= 0;
paramconstraints = [evalsOutUC nonnegsig1 ...
nonnegsig2 nonnegsig3];
if sum(paramconstraints) > 0
logprior = -Inf;
else
logprior = 0; % Prior density is proportional to 1 for all values
% in the parameter space.
end
end
Create a time-varying, Bayesian state-space model that uses the structure of the DGP.
Mdl = bssm(@(params)timeVariantParamMapBayes(params,numObs),@flatPriorBSSM);
Draw a sample from the posterior distribution. Initialize the parameter values to a random set of positive values in [0,0.5]. Set the proposal distribution to multivariate with a scale matrix proportional. Set the proportionality constant to 0.005.
params0 = 0.5*rand(numParams,1); options = optimoptions("fminunc",Display="off"); [params0,Proposal] = tune(Mdl,y,params0,Options=options,Display=false); [PostParams,accept] = simulate(Mdl,y,params0,Proposal, ... DoF=25,Proportion=0.005); accept
accept = 0.7460
PostParams is an 8-by-1000 matrix of 1000 random draws from the posterior distribution. The Metropolis-Hastings sampler accepted 75% of the proposed draws.
When you work with a state-space model that contains a deflated response variable, you must have data for the predictors.
Consider a regression of the US unemployment rate onto and real gross national product (rGNP) rate, and suppose the resulting innovations are an ARMA(1,1) process. The state-space form of the relationship is
where:
is the ARMA process.
is a dummy state for the MA(1) effect.
is the observed unemployment rate deflated by a constant and the rGNP rate ().
is an iid Gaussian series with mean 0 and standard deviation 1.
Load the Nelson-Plosser data set, which contains a table DataTable that has the unemployment rate and rGNP series, among other series.
load Data_NelsonPlosserCreate a variable in DataTable that represents the returns of the raw rGNP series. Because price-to-returns conversion reduces the sample size by one, prepad the series with NaN.
DataTable.RGNPRate = [NaN; price2ret(DataTable.GNPR)]; T = height(DataTable);
Create variables for the regression. Represent the unemployment rate as the observation series and the constant and rGNP rate series as the deflation data .
Z = [ones(T,1) DataTable.RGNPRate]; y = DataTable.UR;
Write a function that specifies how the parameters theta, response series y, and deflation data Z map to the state-space model matrices, the initial state moments, and the state types. Save this code as a file named armaDeflateYBayes.m on your MATLAB® path. Alternatively, open the example to access the function.
type armaDeflateYBayes.m% Copyright 2022 The MathWorks, Inc.
function [A,B,C,D,Mean0,Cov0,StateType,DeflatedY] = armaDeflateYBayes(theta,y,Z)
% Time-invariant, Bayesian state-space model parameter mapping function
% example. This function maps the vector parameters to the state-space
% matrices (A, B, C, and D), the default initial state value and the
% default initial state variance (Mean0 and Cov0), the type of state
% (StateType), and the deflated observations (DeflatedY). The log prior
% distribution enforces parameter constraints (see flatPriorDeflateY.m).
A = [theta(1) theta(2); 0 0];
B = [theta(3); 1];
C = [1 0];
D = 0;
Mean0 = [];
Cov0 = [];
StateType = [0 0];
DeflatedY = y - Z*[theta(4); theta(5)];
end
Write a function that specifies a flat prior distribution on the state-space model parameters theta. The function returns the scalar log prior for an input set of parameters. Save this code as a file named flatPriorDeflateY.m on your MATLAB® path. Alternatively, open the example to access the function.
type flatPriorDeflateY.m% Copyright 2022 The MathWorks, Inc.
function logprior = flatPriorDeflateY(theta)
% flatPriorDeflateY computes the log of the flat prior density for the five
% variables in theta (see armaDeflateYBayes.m). Log probabilities
% for parameters outside the parameter space are -Inf.
% theta(1) and theta(2) are the AR and MA terms in a stationary
% ARMA(1,1) model. The AR term must be within the unit circle.
AROutUC = abs(theta(1)) >= 1;
% The standard deviation of innovations (theta(3)) must be positive.
nonnegsig1 = theta(3) <= 0;
paramconstraints = [AROutUC nonnegsig1];
if sum(paramconstraints) > 0
logprior = -Inf;
else
logprior = 0; % Prior density is proportional to 1 for all values
% in the parameter space.
end
end
Create a bssm object representing the Bayesian state-space model. Specify the parameter-to-matrix mapping function as a handle to a function solely of the parameters.
numParams = 5; Mdl = bssm(@(params)armaDeflateYBayes(params,y,Z),@flatPriorDeflateY)
Mdl =
Mapping that defines a state-space model:
@(params)armaDeflateYBayes(params,y,Z)
Log density of parameter prior distribution:
@flatPriorDeflateY
Draw a sample from the posterior distribution. Initialize the MCMC algorithm with a random set of positive values in [0,0.5]. Obtain an optimal set of proposal distribution moments for the sampler by using tune. Set the proportionality constant to 0.01. Set a burn-in period of 2000 draws, set a thinning factor of 50, and specify retaining 1000 draws.
rng(1) % For reproducibility params0 = 0.5*rand(numParams,1); options = optimoptions("fminunc",Display="off"); [params0,Proposal] = tune(Mdl,y,params0,Options=options, ... Display=false); [PostParams,accept] = simulate(Mdl,y,params0,Proposal,Proportion=0.01, ... BurnIn=2000,NumDraws=1000,Thin=50); accept
accept = 0.9200
PostParams is a 5-by-1000 matrix of 1000 draws from the posterior distribution. The Metropolis-Hastings sampler accepts 92% of the proposed draws.
paramNames = ["\phi" "\theta" "\sigma" "\beta_0" "\beta_1"]; figure h = tiledlayout(numParams,1); for j = 1:numParams nexttile plot(PostParams(j,:)) hold on ylabel(paramNames(j)) end title(h,"Posterior Trace Plots")

All samples appear to suffer from autocorrelation. To improve the Markov chain, experiment with the Thin option.
The estimate and simulate functions do not return posterior draws of the degrees of freedom parameters of multivariate t-distributed state disturbances and observation innovations. However, you can write an output function that stores the degrees of freedom draws at each iteration of the MCMC algorithm, and pass it to simulate to obtain the draws.
Consider the following DGP.
The true value of the state-space parameter set .
The state disturbances and are jointly a multivariate Student's random series with degrees of freedom.
Create a vector autoregression (VAR) model that represents the state equation of the DGP.
trueTheta = [0.5; -0.75; 1; 0.5];
trueDoF = 5;
phi = [trueTheta(1) 0; 0 trueTheta(2)];
Sigma = [trueTheta(3)^2 0; 0 trueTheta(4)^2];
DGP = varm(AR={phi},Covariance=Sigma,Constant=[0; 0]);Filter a random 2-D multivariate central series of length 500 through the VAR model to obtain state values. Set the degrees of freedom to 5.
rng(10) % For reproducibility
T = 500;
trueU = mvtrnd(eye(DGP.NumSeries),trueDoF,T);
X = filter(DGP,trueU);Obtain a series of observations from the DGP by the linear combination .
C = [1 3]; y = X*C';
Consider a Bayesian state-space model representing the model with parameters and treated as unknown. Arbitrarily assume that the prior distribution of the parameters in are independent Gaussian random variables with mean 0.5 and variance 1. Assume that the prior on the degrees of freedom is flat. The functions in Local Functions specify the state-space structure and prior distributions.
Create the Bayesian state-space model by passing function handles to the paramMap and priorDistribution functions to bssm. Specify that the state disturbance distribution is multivariate Student's with unknown degrees of freedom.
PriorMdl = bssm(@paramMap,@priorDistribution,StateDistribution="t");PriorMdl is a bssm object representing the Bayesian state-space model with unknown parameters.
In Local Functions, write a function called posteriorDrawsNuU that accepts the input structure and returns the posterior draws of .
function StateDoF = posteriorDrawsStateDoF(inputstruct) StateDoF = inputstruct.StateDoF; end
Simulate draws from the posterior distribution of by using simulate. Specify a random set of positive values in [0,1] to initialize the Kalman filter.
Set the burn-in period of the MCMC algorithm to 1000 draws, draw a sample of 10000 from the posterior, specify the univariate treatment of multivariate series for faster computations, and set the proposal scale matrix to a diagonal matrix with small values along the diagonal to increase the proposal acceptance rate.
numParamsTheta = 4; theta0 = rand(numParamsTheta,1); [ThetaPostDraws,accept,StateDoFDraws] = simulate(PriorMdl,y,theta0, ... eye(numParamsTheta)/1000,BurnIn=1e3,NumDraws=1e4, ... Univariate=true,OutputFunction=@posteriorDrawsStateDoF); [numThetaParams,numDraws] = size(ThetaPostDraws)
numThetaParams = 4
numDraws = 10000
accept
accept = 0.4066
size(StateDoFDraws)
ans = 1×2
1 10000
ThetaPostDraws is a 4-by-10000 matrix containing the posterior draws of the parameters . accept is the Metropolis-Hastings sampler acceptance probability, in this case 41%, which means that simulate rejected 59% of the posterior draws. StateDoFDraws is a 1-by-10000 vector containing the posterior draws of .
To diagnose the Markov chain induced by the Metropolis-within-Gibbs sampler, create a trace plot of the posterior draws of .
figure
plot(StateDoFDraws)
title("Posterior Trace Plot of \nu_u")
The posterior sample shows significant serial correlation. You can remedy these behaviors by adjusting the Thin name-value argument. In general, simulate has name-value arguments that enable you to control several aspects of the MCMC sampler, which can improve the quality of the posterior sample.
Local Functions
This example uses the following functions. paramMap is the parameter-to-matrix mapping function and priorDistribution is the log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = [theta(1) 0; 0 theta(2)]; B = [theta(3) 0; 0 theta(4)]; C = [1 3]; D = 0; Mean0 = []; % MATLAB uses default initial state mean Cov0 = []; % MATLAB uses initial state covariances StateType = [0; 0]; % Two stationary states end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta(1)) >= 1) (abs(theta(2)) >= 1) ... (theta(3) < 0) (theta(4) < 0)]; if(sum(paramconstraints)) logprior = -Inf; else mu0 = 0.5*ones(numel(theta),1); sigma0 = 1; p = normpdf(theta,mu0,sigma0); logprior = sum(log(p)); end end function StateDoF = posteriorDrawsStateDoF(inputstruct) StateDoF = inputstruct.StateDoF; end
Input Arguments
Observed response data, from which simulate forms the
posterior distribution, specified as a numeric matrix or a cell vector of numeric vectors.
If
PriorMdlis time invariant with respect to the observation equation,Yis a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row ofYcontains the latest observations.If
PriorMdlis time varying with respect to the observation equation,Yis a T-by-1 cell vector.Y{t}contains an nt-dimensional vector of observations for period t, where t = 1, ..., T. The corresponding dimensions of the coefficient matrices, outputs ofPriorMdl.ParamMap,C{t}, andD{t}must be consistent with the matrix inY{t}for all periods. The last cell ofYcontains the latest observations.
NaN elements indicate missing observations. For details on how the
Kalman filter accommodates missing observations, see Algorithms.
Data Types: double | cell
Initial parameter values for the parameters Θ, specified as a
numParams-by-1 numeric vector. Elements of
params0 must correspond to the elements of the first input
arguments of PriorMdl.ParamMap and
PriorMdl.ParamDistribution.
Data Types: double
MH sampler proposal distribution covariance/scale matrix for the parameters Θ, up to
the proportionality constant Proportion, specified as a
numParams-by-numParams, positive-definite
numeric matrix. Elements of Proposal must correspond to elements in
params0.
The proposal distribution is multivariate normal or Student's t
with DoF degrees of freedom (for details, see
DoF).
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: simulate(Mdl,Y,params0,Proposal,NumDraws=1e6,Thin=3,DoF=10)
uses the multivariate t10 distribution for the
Metropolis-Hastings proposal, draws 3e6 random vectors of parameters, and
thins the sample to reduce serial correlation by discarding every 2 draws until it retains
1e6 draws.
Kalman Filter Options
Univariate treatment of a multivariate series flag, specified as a value in this table.
| Value | Description |
|---|---|
true | Applies the univariate treatment of a multivariate series, also known as sequential filtering |
false | Does not apply sequential filtering |
The univariate treatment can accelerate and improve numerical stability of the Kalman filter.
However, all observation innovations must be uncorrelated. That is,
DtDt'
must be diagonal, where Dt
(t = 1, ..., T) is the output coefficient
matrix D of PriorMdl.ParamMap and
PriorMdl.ParamDistribution.
Example: Univariate=true
Data Types: logical
Square root filter method flag, specified as a value in this table.
| Value | Description |
|---|---|
true | Applies the square root filter method for the Kalman filter |
false | Does not apply the square root filter method |
If you suspect that the eigenvalues of the filtered state or forecasted observation covariance
matrices are close to zero, then specify SquareRoot=true. The square
root filter is robust to numerical issues arising from the finite precision of
calculations, but requires more computational resources.
Example: SquareRoot=true
Data Types: logical
Posterior Sampling Options
Number of Metropolis-Hastings sampler draws from the posterior distribution Π(θ|Y), specified as a positive integer.
Example: NumDraws=1e7
Data Types: double
Number of draws to remove from the beginning of the sample to reduce transient effects,
specified as a nonnegative scalar. For details on how simulate
reduces the full sample, see Algorithms.
Tip
To help you specify the appropriate burn-in period size:
Determine the extent of the transient behavior in the sample by setting the
BurnInname-value argument to0.Simulate a few thousand observations by using
simulate.Create trace plots.
Example: BurnIn=1000
Data Types: double
Adjusted sample size multiplier, specified as a positive integer.
The actual sample size is BurnIn +
NumDraws*Thin. After discarding the burn-in,
simulate discards every Thin –
1 draws, and then retains the next draw. For more details on how
simulate reduces the full sample, see Algorithms.
Tip
To reduce potential large serial correlation in the posterior sample, or to reduce the memory
consumption of the output sample, specify a large
value for Thin.
Example: Thin=5
Data Types: double
Proposal distribution degrees of freedom for parameter updates using the MH sampler, specified as a value in this table.
| Value | MH Proposal Distribution |
|---|---|
| Positive scalar | Multivariate t with DoF degrees
of freedom |
Inf | Multivariate normal |
The following options specify other aspects of the proposal distribution:
Proposal— Required covariance/scale matrixProportion— Optional proportionality constant that scalesProposalCenter— Optional expected valueStdDoF— Optional proposal standard deviation of the degrees of freedom parameter of the t-distributed state disturbance or observation innovation process
Example: DoF=10
Data Types: double
Proposal scale matrix proportionality constant, specified as a positive scalar.
Tip
For higher proposal acceptance rates, experiment with relatively small values for Proportion.
Example: Proportion=1
Data Types: double
Proposal distribution center, specified as a value in this table.
| Value | Description |
|---|---|
numParams-by-1 numeric vector | simulate uses the independence Metropolis-Hastings sampler. Center is the center of the proposal distribution. |
[] (empty array) | simulate uses the random-walk Metropolis-Hastings sampler. The center of the proposal density is the current state of the Markov chain. |
Example: Center=ones(10,1)
Data Types: double
Proposal standard deviation for the degrees of freedom parameter of the t-distributed state disturbance or observation innovation process, specified as a positive numeric scalar.
StdDoF applies to the corresponding process when
PriorMdl.StateDistribution.Name is "t" or
PriorMdl.ObservationDistribution.Name is "t",
and their associated degrees of freedom are estimable (the DoF field
is NaN or a function handle). For example, if the following
conditions hold, StdDof applies only to the
t-distribution degrees of freedom of the state disturbance process:
PriorMdl.StateDistribution.Nameis"t".PriorMdl.StateDistribution.DoFisNaN.The limiting distribution of the observation innovations is Gaussian (
PriorMdl.ObservationDistribution.Nameis"Gaussian"orPriorMdl.ObservationDistributionisstruct("Name","t","DoF",Inf).
Example: StdDoF=0.5
Data Types: double
Function that simulate calls after each MCMC iteration,
specified as a function handle. simulate saves the outputs of
the specified function after each iteration and returns them in the
Output output argument. You write the function, which can
perform arbitrary calculations, such as computing or plotting custom statistics at
each iteration.
Suppose outputfcnoutputfcn
function Output = outputfcn(Input) ... end
simulate passes
Input| Field | Description | Value |
|---|---|---|
Iteration | Current iteration | Numeric scalar |
Parameters | Current values of the parameters θ | Numeric vector |
LogPosteriorDensity | Log posterior density evaluated at current parameters and conditioned on latent variables | Numeric scalar |
StateDoF | Current degree of freedom of the t-distributed state disturbances | Numeric scalar |
ObservationDoF | Current degree of freedom of the t-distributed observation innovation | Numeric scalar |
StateVariance | Current latent variance variable associated with the state disturbance | T-by-1 numeric vector |
ObservationVariance | Current latent variance variable associated with the observation innovation | T-by-1 numeric vector |
Mixture | Gaussian mixture distribution hyperparameters for finite Gaussian mixture observation innovations | Structure array equal to
PriorMdl.ObservationDistribution |
LatentClass | Current latent regime variable for finite-Gaussian-mixture observation innovations | T-by-1 numeric vector |
Intercept | Current observation deflator factor for finite-Gaussian-mixture or skew-normal observation innovations | T-by-1 numeric vector |
Delta | Current shape hyperparameter δ for skew normal observation innovations | Numeric scalar |
A | Coefficient A evaluated at current parameters | Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient |
B | Coefficient B evaluated at current parameters | Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient |
C | Coefficient C evaluated at current parameters | Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient |
D | Coefficient D evaluated at current parameters | Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient |
States | Current state draws obtained by simulation smoother | Numeric matrix for a dimension-invariant coefficient or a T-by-1 cell vector of numeric matrices for a dimension-varying coefficient |
Y | Observations | The value of the input Y |
PreviousOutput | Output of the previous iteration | Structure array with fields in this table |
OutputoutputfcnOutputsimulate
concatenates the outputs of all iterations and returns a
k-by-NumDraws matrix of the same type. If
simulate cannot horizontally concatenate the outputs of all
iterations, simulate returns a
1-by-NumDraws cell array instead, where successive cells contain
the output of corresponding iterations.
Example: OutputFunction=@outputfcn
Data Types: function_handle
Output Arguments
Proposal acceptance rate, returned as a positive scalar in [0,1].
Custom function OutputFunction output concatenated over all MCMC iterations, returned as a matrix or cell vector. Output has NumDraws columns, and the number of rows depends on the size of the output at each iteration. The data type of the entries of Output depends on the operations of the output function.
More About
To facilitate posterior sampling, multivariate Student's t-distributed state disturbances and observation innovations are each represented as an inverse-gamma scale mixture, where the inverse-gamma random variable is the latent variance variable.
Explicitly, suppose the m-dimensional state disturbances ut are iid multivariate t distributed with location 0, scale Im, and degrees of freedom νu. As an inverse-gamma scale mixture
where:
The latent variable ζt is inverse-gamma with shape and scale νu/2.
is an m-dimensional multivariate standard Gaussian random variable.
Multivariate t-distributed observation innovations can be similarly decomposed.
You can access ζt by writing a custom output
function that returns the field for the specified error type, either
StateVariance or ObservationVariance. For more
details, see the OutputFunction name-value argument and
Output output argument.
The latent regime variable
zt is a discrete random variable that describes
the probability distribution of randomly selecting one of the r regimes
of the Gaussian mixture distribution. It is a latent component of a hierarchical
representation of finite-Gaussian-mixture-distributed observation innovations
εt. The sample space of
zt is 1,…,r and
P(zt = j)
= wj, where
wj =
PriorMdl.Distribution.Weight(j
Suppose univariate εt is a series of iid finite Gaussian mixture distributed random variables with r regimes, weight or probability vector w, mean vector μ, and variance vector σ2. At time t and given zt = j, εt has a Gaussian distribution with mean μj and variance σ2j. Therefore, the distribution of εt is
bssm functions use this representation to facilitate posterior
sampling from by the Metropolis-within-Gibbs sampler:
Condition on zt = j and yt and use the results of the Kalman filter to sample from
Evaluate where p(θ) is the prior specified by
PriorMdland p(yt|θ,zt) is a result of the Kalman filter.Update θ using the Metropolis-Hastings sampler.
Update the states according to p(xt|θ,yt,zt) by using the simulation smoother.
Update zt from a categorical distribution according to
You can access zt by writing a
custom output function that returns the LatentClass field. For more
details, see the OutputFunction name-value argument and
Output output argument.
In general, an observation deflator factor dt in a state-space model is a factor in the term subtracted from the observation yt to ensure the mean of the observation equation, re-expressed in terms of the deflated observation is Ctxt. This deflation helps identify the states in the observation equation for state and parameter estimation.
bssm functions deflate observations when the observation innovation
variable εt has one of the following distributions:
Finite Gaussian mixture — For a given latent class zt = j, dt = μj.
Skew normal — where are the series of residuals scaled by Dt and ζɑt is a randomly drawn value from the truncated normal distribution, with support (0,∞), derived from a Gaussian distribution with a mean of and a variance of (
simulatedetermines the intercept during posterior sampling).
Regardless of observation-innovation distribution,
simulate deflates the observations by . You can access dt by writing a
custom output function that returns the Intercept field. For more
details, see the OutputFunction name-value
argument and Output output argument.
Tips
Acceptance rates from
acceptthat are relatively close to 0 or 1 indicate that the Markov chain does not sufficiently explore the posterior distribution. To obtain an appropriate acceptance rate for your data, tune the sampler by implementing one of the following procedures.Use the
tunefunction to search for the posterior mode by numerical optimization.tunereturns optimized parameters and the proposal scale matrix, which is proportional to the negative Hessian matrix evaluated at the posterior mode. Pass the optimized parameters and the proposal scale tosimulate, and tune the proportionality constant by using theProportionname-value argument. Small values ofProportiontend to increase the proposal acceptance rates of the MH sampler.Perform a multistage simulation:
Choose an initial value for the input
Proposaland simulate draws from the posterior.Compute the sample covariance matrix, and pass the result to
simulateas an updated value forProposal.Repeat steps 1 and 2 until
acceptis reasonable for your data.
Algorithms
simulateperforms posterior simulation of model parameters, states, and latent variables as follows:simulategenerates parameter draws by the Metropolis-Hastings sampler. The posterior density is proportional to the product of the prior densityPriorMdl.ParamDistributionand the likelihood obtained by the Kalman filter of the state-space modelPriorMdl.ParamMap.simulateupdates states by the simulation smoother of the state-space model.simulatesamples the latent variance variables of state disturbance and observation innovation distributions from posterior conditional distributions. For t-distributed state disturbances or observation innovations, latent variables are inverse-gamma distributed.
If the input prior model
PrioirMdlis a Gaussian linear state-space model and you do not specify the custom output functionOutputFunction,simulatemarginalizes the states, and the Metropolis-Hastings sampler simulates only parameters. Otherwise,simulatesimulates parameters Θ, states xt, and latent variables ζt by the Metropolis-within-Gibbs sampler, which is more computationally intensive compared to the standard Metropolis-Hastings sampler.This figure shows how
simulatereduces the sample by using the values ofNumDraws,Thin, andBurnIn. Rectangles represent successive draws from the distribution.simulateremoves the white rectangles from the sample. The remainingNumDrawsblack rectangles compose the sample.
References
[1] Hastings, Wilfred K. "Monte Carlo Sampling Methods Using Markov Chains and Their Applications." Biometrika 57 (April 1970): 97–109. https://doi.org/10.1093/biomet/57.1.97.
[2] Metropolis, Nicholas, Rosenbluth, Arianna. W., Rosenbluth, Marshall. N., Teller, Augusta. H., and Teller, Edward. "Equation of State Calculations by Fast Computing Machines." The Journal of Chemical Physics 21 (June 1953): 1087–92. https://doi.org/10.1063/1.1699114.
Version History
Introduced in R2022a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)