La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.
Identification de modèles boîte noire non linéaires avec l’application System Identification
Introduction
Objectifs
Estimer et valider des modèles non linéaires à partir de données à entrée unique/sortie unique (SISO) pour trouver celui qui représente le mieux la dynamique du système.
À la fin de ce tutoriel, vous serez capable d’accomplir les tâches suivantes avec l’application System Identification :
Importer des objets de données depuis l’espace de travail MATLAB® dans l’application.
Estimer et valider des modèles non linéaires à partir des données.
Tracer et analyser le comportement des non-linéarités.
Description des données
Ce tutoriel utilise le fichier de données twotankdata.mat, qui contient les données SISO dans le domaine temporel du système à deux cuves représenté sur la figure suivante.
Système à deux cuves
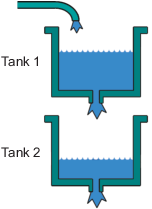
Dans le système à deux cuves, l’eau se déverse à travers un tuyau dans la cuve 1, s’écoule dans la cuve 2 et quitte le système à travers un petit trou au fond de la cuve 2. L’entrée mesurée u(t) du système est la tension appliquée à la pompe qui alimente en eau la cuve 1 (en volts). La sortie mesurée y(t) est la hauteur d’eau dans la cuve inférieure (en mètres).
D’après le théorème de Bernoulli, qui énonce que l’eau s’écoulant à travers un petit trou au fond d’un réservoir dépend du niveau d’eau dans la cuve selon une formule non linéaire, vous prévoyez que la relation entre les données d’entrée et de sortie est non linéaire.
twotankdata.mat inclut 3 000 échantillons avec un pas d’échantillonnage de 0,2 s.
Quels sont les modèles boîte noire non linéaires ?
Types de modèles boîte noire non linéaires
Vous pouvez estimer des modèles boîte noire à temps discret non linéaires pour des données à sortie unique et à sorties multiples dans le domaine temporel. Vous pouvez choisir parmi deux types de structure de modèle boîte noire non linéaire :
Modèles ARX non linéaires
Modèles de Hammerstein-Wiener
Remarque
Vous pouvez estimer des modèles boîte noire de Hammerstein-Wiener à partir uniquement de données d’entrée/sortie. Ces modèles ne supportent pas les données de séries temporelles sans entrée.
Pour plus d'informations sur l’estimation de modèles boîte noire non linéaires, consultez Identification de modèles non linéaires.
Qu’est-ce qu’un modèle ARX non linéaire ?
Un modèle ARX non linéaire se compose des variables explicatives d'un modèle et d’une fonction de sortie. La fonction de sortie contient un ou plusieurs objets de correspondance, un pour chaque entrée du modèle. Chaque objet de correspondance peut inclure une fonction linéaire ou non linéaire qui agit sur les variables explicatives du modèle pour donner la sortie du modèle et un décalage fixe pour cette sortie. Ce schéma bloc représente la structure d’un modèle ARX non linéaire à entrée unique dans un scénario de simulation.
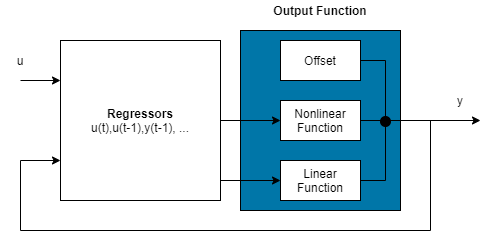
Le software calcule la sortie du modèle ARX non linéaire y en deux étapes :
Il calcule les valeurs des variables explicatives à partir des valeurs d’entrée actuelles et passées et des données de sortie passées.
Dans le cas le plus simple, les variables explicatives sont des entrées et des sorties retardées, comme u(t–1) et y(t–3). Les variables explicatives de ce type sont appelées variables explicatives linéaires. Vous spécifiez des variables explicatives linéaires avec l’objet
linearRegressor. Vous pouvez également spécifier des variables explicatives linéaires en utilisant des ordres de modèle ARX linéaire comme arguments d’entrée. Pour plus d’informations, consultez Nonlinear ARX Model Orders and Delay. Cependant, cette deuxième approche limite votre jeu de variables explicatives à des variables explicatives linéaires avec des retards consécutifs. Pour créer des variables explicatives polynomiales, utilisez l’objetpolynomialRegressor. Pour créer des variables explicatives périodiques contenant des fonctions sinus et cosinus de variables d’entrée et de sortie retardées, utilisez l’objetperiodicRegressor. Vous pouvez également spécifier des variables explicatives personnalisées, qui sont des fonctions non linéaires d’entrées et de sorties retardées. Par exemple, u(t–1)y(t–3) est une variable explicative personnalisée qui multiplie ensemble des instances d’entrée et de sortie. Spécifiez des variables explicatives personnalisées avec l’objetcustomRegressor.Vous pouvez attribuer n’importe quelle variable explicative comme entrée du bloc de fonction linéaire de la fonction de sortie, du bloc de fonction non linéaire ou des deux.
Il établit une correspondance entre les variables explicatives et la sortie du modèle avec un bloc de fonction de sortie. Le bloc de fonction de sortie peut inclure plusieurs objets de correspondance avec chacun un objet de correspondance contenant des blocs linéaires, non linéaires et de décalage (offset) en parallèle. Par exemple, considérez l’équation suivante :
Ici, x est un vecteur des variables explicatives et r est la moyenne de x. est la sortie du bloc de fonction linéaire. représente la sortie du bloc de fonction non linéaire. Q est une matrice de projection qui permet que les calculs soient bien conditionnés. d est un décalage scalaire qui est ajouté aux sorties combinées des blocs linéaires et non linéaires. La forme exacte de F(x) dépend de la fonction de sortie que vous avez choisie. Vous pouvez faire une sélection parmi les objets de correspondance disponibles, comme des réseaux de partition en arborescence, des réseaux d’ondelettes et des réseaux de neurones multicouches. Vous pouvez également exclure le bloc de fonction linéaire ou non linéaire de la fonction de sortie.
Lors de l’estimation d’un modèle ARX non linéaire, le software calcule les valeurs des paramètres du modèle, comme L, r, d, Q, et d’autres paramètres spécifiant g.
Les modèles ARX non linéaires résultants sont des objets idnlarx qui enregistrent toutes les données du modèle, y compris les variables explicatives et les paramètres de la fonction de sortie. Pour plus d'informations sur ces objets, consultez Nonlinear Model Structures.
Qu'est-ce qu'un modèle de Hammerstein-Wiener ?
Ce schéma bloc représente la structure d’un modèle de Hammerstein-Wiener :

Où
f est une fonction non linéaire qui transforme les données d’entrée u(t) selon w(t) = f(u(t)).
w(t), une variable interne, est la sortie du bloc Input Nonlinearity et a la même dimension que u(t).
B/F est une fonction de transfert linéaire qui transforme w(t) selon x(t) = (B/F)w(t).
x(t), une variable interne, est la sortie du bloc linéaire et a la même dimension que y(t).
B et F sont similaires à des polynômes dans un modèle Output-Error linéaire. Pour plus d'informations sur les modèles Output-Error, consultez What Are Polynomial Models?.
Pour ny sorties et nu entrées, le bloc linéaire est une matrice de fonction de transfert contenant des entrées :
où j =
1,2,...,nyet i =1,2,...,nu.h est une fonction non linéaire qui établit une correspondance entre la sortie du bloc linéaire x(t) et la sortie du système y(t) selon y(t) = h(x(t)).
Comme f agit sur le port d’entrée du bloc linéaire, cette fonction est appelée input nonlinearity. De même, comme h agit sur le port de sortie du bloc linear, cette fonction est appelée output nonlinearity. Si votre système contient plusieurs entrées et sorties, vous devez définir les fonctions f et h pour chaque signal d’entrée et de sortie. Vous n’êtes pas obligé d’inclure à la fois la non-linéarité d’entrée et la non-linéarité de sortie dans la structure de modèle. Si un modèle contient uniquement la non-linéarité d’entrée (Input Nonlinearity) f, il est appelé modèle de Hammerstein. De même, si un modèle contient uniquement la non-linéarité de sortie (Output Nonlinearity)h, il est appelé modèle de Wiener.
Le software calcule la sortie du modèle de Hammerstein-Wiener y en trois étapes :
Il calcule w(t) = f(u(t)) à partir des données d’entrée.
w(t) est une entrée de la fonction de transfert linéaire B/F.
La non-linéarité d’entrée est une fonction statique (sans mémoire), où la valeur de la sortie à un instant t donné dépend uniquement de la valeur d’entrée à l’instant t.
Vous pouvez configurer la non-linéarité d’entrée sous forme de réseau sigmoïde, de réseau d’ondelettes, de saturation, de zone morte, de fonction linéaire par morceaux, de polynôme unidimensionnel ou de réseau personnalisé. Vous pouvez également supprimer la non-linéarité d’entrée.
Il calcule la sortie du bloc linéaire à l’aide de w(t) et des conditions initiales : x(t) = (B/F)w(t).
Vous pouvez configurer le bloc linéaire en spécifiant les ordres du numérateur B et du dénominateur F.
Il calcule la sortie du modèle en transformant la sortie du bloc linéaire x(t) à l’aide de la fonction non linéaire : h selon y(t) = h(x(t)).
Comme la non-linéarité d’entrée, la non-linéarité de sortie est une fonction statique. Vous pouvez configurer la non-linéarité de sortie de la même manière que la non-linéarité d’entrée. Vous pouvez également supprimer la non-linéarité de sortie, de sorte que y(t) = x(t).
Les modèles résultants sont des objets idnlhw qui enregistrent toutes les données du modèle, y compris les paramètres du modèle et les estimateurs de non-linéarité. Pour plus d'informations sur ces objets, consultez Nonlinear Model Structures.
Préparation des données
Charger les données dans l'espace de travail MATLAB
Chargez les données d’échantillons dans twotankdata.mat en saisissant la commande suivante dans la fenêtre de commande MATLAB :
load twotankdata
Cette commande charge les deux variables suivantes dans le panneau de l’espace de travail MATLAB :
uest la donnée d’entrée, qui est la tension appliquée à la pompe qui alimente en eau la cuve 1 (en volts).yest la donnée de sortie, qui est la hauteur d’eau dans la cuve 2 (en mètres).
Créer des objets iddata
Les objets de données System Identification Toolbox™ encapsulent les valeurs des données et leurs propriétés dans une seule entité. Vous pouvez utiliser les commandes de System Identification Toolbox pour manipuler aisément ces objets de données comme des entités uniques.
Vous devez avoir déjà chargé les données d’échantillon dans l’espace de travail MATLAB, comme décrit dans Charger les données dans l'espace de travail MATLAB.
Utilisez les commandes suivantes pour créer deux objets de données iddata, ze et zv, où ze contient des données pour l’estimation du modèle et zv contient des données pour la validation du modèle. Ts est le pas d'échantillonnage.
Ts = 0.2; % Sample time is 0.2 sec z = iddata(y,u,Ts); % First 1000 samples used for estimation ze = z(1:1000); % Remaining samples used for validation zv = z(1001:3000);
Pour visualiser les propriétés de l’objet iddata, utilisez la commande get. Par exemple :
get(ze)
Le software MATLAB renvoie les propriétés et les valeurs des données suivantes :
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x1 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []Pour modifier les propriétés des données, utilisez la notation par points. Par exemple, pour attribuer aux canaux des noms et des unités qui étiquettent les axes du graphique, saisissez la syntaxe suivante dans la fenêtre de commande MATLAB :
% Set time units to minutes ze.TimeUnit = 'sec'; % Set names of input channels ze.InputName = 'Voltage'; % Set units for input variables ze.InputUnit = 'V'; % Set name of output channel ze.OutputName = 'Height'; % Set unit of output channel ze.OutputUnit = 'm'; % Set validation data properties zv.TimeUnit = 'sec'; zv.InputName = 'Voltage'; zv.InputUnit = 'V'; zv.OutputName = 'Height'; zv.OutputUnit = 'm';
Pour vérifier que la propriété InputName de ze est modifiée, saisissez la commande suivante :
ze.inputname
Conseil
Les noms de propriétés, comme InputName, ne sont pas sensibles à la casse. Vous pouvez également abréger les noms de propriétés qui commencent par Input ou Output en remplaçant u par Input et y par Output dans le nom de la propriété. Par exemple, OutputUnit est équivalent à yunit.
Démarrer l’application System Identification
Pour ouvrir l’application System Identification, saisissez la commande suivante dans la fenêtre de commande MATLAB :
systemIdentification
Le nom de session par défaut Untitled apparaît dans la barre de titre.

Importation d’objets de données dans l’application System Identification
Vous pouvez importer les objets de données dans l’application depuis l’espace de travail MATLAB.
Vous devez avoir déjà créé les objets de données, comme décrit dans Créer des objets iddata, et ouvert l’application, comme décrit dans Démarrer l’application System Identification.
Pour importer des objets de données :
Dans l’application System Identification, sélectionnez Import data > Data object.
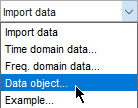
Cette action ouvre la boîte de dialogue Import Data (Importer des données).
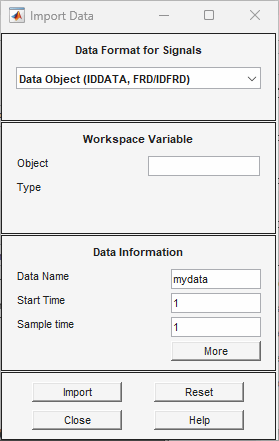
Saisissez
zedans le champ Object pour importer les données d’estimation. Appuyez sur Entrée.Cette action saisit les informations des objets dans les champs Import Data.
Cliquez sur More pour visualiser des informations supplémentaires sur ces données, y compris les noms des canaux et les unités.
Cliquez sur Import pour ajouter l’icône nommée
zeà l’application System Identification.Dans la boîte de dialogue Import Data, saisissez
zvdans le champ Object pour importer les données de validation. Appuyez sur Entrée.Cliquez sur Import pour ajouter l’icône nommée
zvà l’application System Identification.Dans la boîte de dialogue Import Data, cliquez sur Close.
Dans l’application System Identification, faites glisser l’icône de données de validation zv dans le rectangle Validation Data. L’icône de données d’estimation ze est déjà indiquée dans le rectangle Working Data.
Sinon, faites un clic droit sur l’icône
zvpour ouvrir la boîte de dialogue Data/model Info (Info données/modèle). Sélectionnez la case à cocher Use as Validation Data. Cliquez sur Apply, puis sur Close pour ajouterzvau rectangle Validation Data.L’application System Identification ressemble maintenant à la figure suivante.
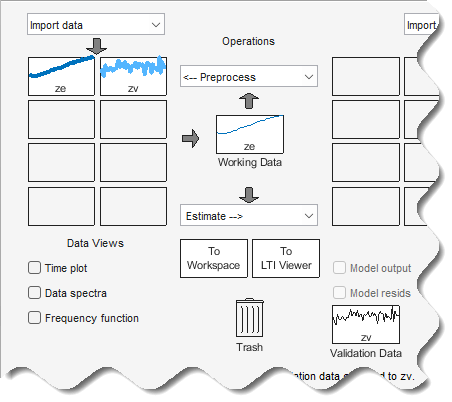
Estimer des modèles ARX non linéaires
Estimer un modèle ARX non linéaire avec des paramètres par défaut
Dans cette partie du tutoriel, vous estimez un modèle ARX non linéaire à l’aide d’une structure de modèle par défaut et d’options d’estimation.
Vous devez avoir déjà préparé les données, comme décrit dans Préparation des données. Pour plus d'informations sur les modèles ARX non linéaires, consultez Qu’est-ce qu’un modèle ARX non linéaire ?.
Remarque
Les illustrations de ce tutoriel représentent une session typique de l’application System Identification. Vos résultats peuvent ne pas correspondre exactement aux résultats sur les images.
Dans l’application System Identification, sélectionnez Estimate > Nonlinear ARX Models.
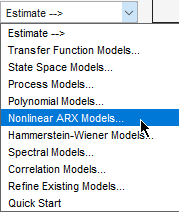
Cette action ouvre la boîte de dialogue Estimate Nonlinear ARX Models.

La boîte de dialogue contient deux onglets : Model Structure et Estimation Options.
L’onglet Model Structure comporte une option d’initialisation au moyen d’un modèle existant. L’onglet contient des paramètres qui configurent la structure du modèle, comme le choix des variables explicatives et le type de fonction de sortie. Spécifiez le nom du modèle à estimer dans Model name. Le nom du modèle par défaut est
nlarx1.Utilisez l’onglet Regressors pour créer les jeux de variables explicatives à utiliser. Par défaut, l’application crée un jeu de variables explicatives linéaires avec des décalages
[1 2]dans chaque variable et enregistre la variable explicative en tant queLinear regressors #1dans le champ Regressor Sets. Ce panneau contient une table qui vous permet de modifier les décalages à utiliser pour chaque variable.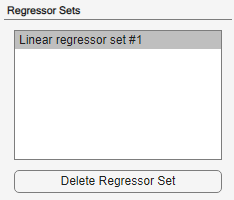
Le panneau de configuration Configure: Linear regressors #1 contient une table qui indique les valeurs de décalage utilisées par le jeu de variables explicatives. Vous pouvez modifier ces décalages.
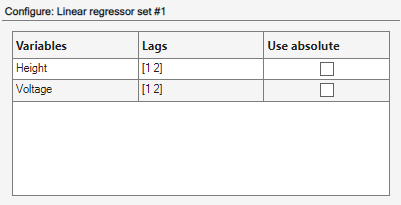
La table d’affectation des variables explicatives Assign Regressors to Output Function liste les noms des variables explicatives et les affectations des variables explicatives aux composantes de la fonction de sortie.
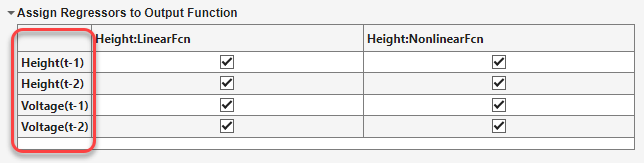
Les affectations des variables explicatives dans la table produisent un modèle pour la sortie
Heightde :Height(t) = f(Height(t-1), Height(t-2),Voltage(t-1),Voltage(t-2))
Ici, f(.) est une fonction non linéaire statique qui établit une correspondance entre les variables explicatives et la sortie. Pour choisir f(.) et ses paramètres associés, utilisez l’onglet Output Function.
Vous pouvez ajouter d’autres jeux de variables explicatives, comme des polynômes et des formules personnalisées, en sélectionnant un type de variable explicative dans Add regressors of type.
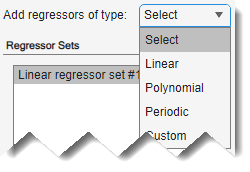
Cet exemple utilise uniquement
Linear regressors #1.Sélectionnez l’onglet Output Function.
L’onglet montre que l’application sélectionne Wavelet Network comme type par défaut de la fonction de sortie f(.). Cette fonction utilise la somme d’une fonction linéaire, d’une fonction non linéaire (qui est une somme d’ondelettes mises à l’échelle) et d’un terme de décalage pour calculer la sortie. L’onglet montre également un jeu de paramètres de configuration. Le nombre d’ondelettes utilisé par la fonction est configuré pour être choisi automatiquement pendant l’estimation. Vous pouvez modifier cette sélection. Pour la première estimation, conservez les choix par défaut.

Cliquez sur Estimate.
Cette action ajoute le modèle
nlarx1au tableau des modèles de l’application System Identification, comme le montre la figure suivante.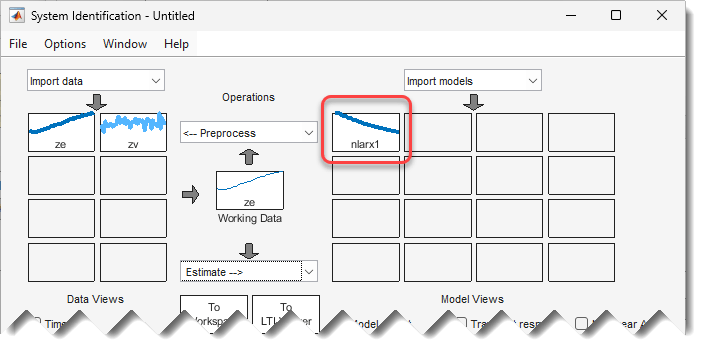
Double-cliquez ou faites un clic droit sur l’icône du modèle
nlarx1. Le tableau des modèles affiche les informations sur le modèle estimé. Le champ supérieur décrit la structure du modèle et les résultats de l’estimation (données utilisées, pourcentage d’ajustement et autres mesures de qualité). Le champ inférieur (Diary and Notes) affiche le script MATLAB que vous pouvez utiliser pour reproduire les résultats de l’estimation en ligne de commande.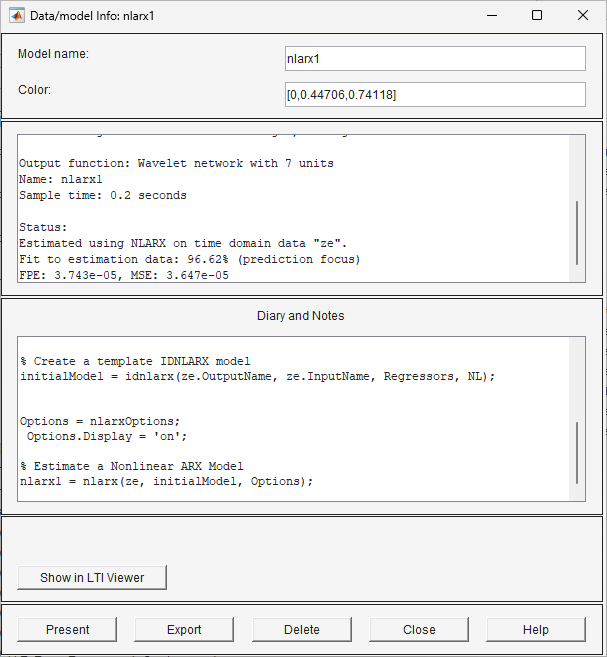
Remarque
Fit (%) est calculé à l’aide du jeu de données d’estimation avec en objectif la prédiction, et non à l’aide du jeu de données de validation. Cependant, le tracé de la sortie du modèle de l’étape suivante compare l’ajustement au jeu de données de validation. Pour voir dans quelle mesure le modèle peut simuler la réponse d’un jeu de données de validation indépendant, utilisez le graphique Model Output, comme le décrit l’étape suivante.
Sélectionnez l’icône du modèle
nlarx1et, dans le champ Model Views de l’application System Identification, sélectionnez Model output. Cette action simule le modèle à l’aide des données de validation d’entrée comme entrée du modèle et trace la sortie simulée au-dessus des données de validation de sortie.
Le champ Best Fits du graphique de la sortie du modèle montre la correspondance entre la sortie du modèle et la sortie des données de validation à l’aide d’une mesure de moyenne quadratique normalisée (NRMS, Normalized Root Mean Squared) du degré d’ajustement. L’ajustement est médiocre dans l’intervalle de temps 400-500.
Tracer des sections transversales de non-linéarité pour des modèles ARX non linéaires
Effectuez la procédure suivante pour visualiser la forme de la non-linéarité comme une fonction des variables explicatives sur un tracé de modèle ARX non linéaire.
Dans l’application System Identification, sélectionnez la case à cocher Nonlinear ARX pour visualiser les sections transversales de non-linéarité.
Par défaut, le tracé montre la relation entre les variables explicatives de sortie
Height(t-1)etHeight(t-2). Ce tracé montre un plan régulier sur la figure suivante. Ainsi, la relation entre les variables explicatives et la sortie est approximativement un plan linéaire.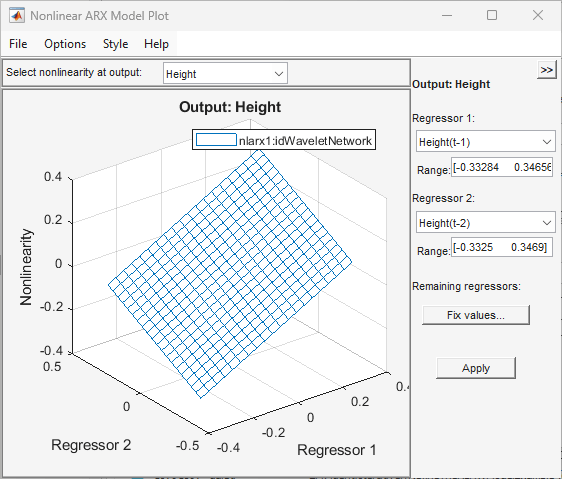
Dans la fenêtre Nonlinear ARX Model Plot, réglez Regressor 1 sur
Voltage(t-1). Réglez Regressor 2 surVoltage(t-2). Cliquez sur Apply.La relation entre ces variables explicatives et la sortie est non linéaire, comme le montre le graphique suivant.

Pour faire tourner la surface de non-linéarité, sélectionnez Style > Rotate 3D et faites glisser le graphique dans une nouvelle orientation.
Pour afficher une section transversale 1-D pour la variable explicative 1, réglez Regressor 2 sur
none, puis cliquez sur Apply. La figure suivante montre l’amplitude de non-linéarité résultante pour la variable explicative 1, qui représente le signal de tension décalé dans le tempsVoltage(t-1).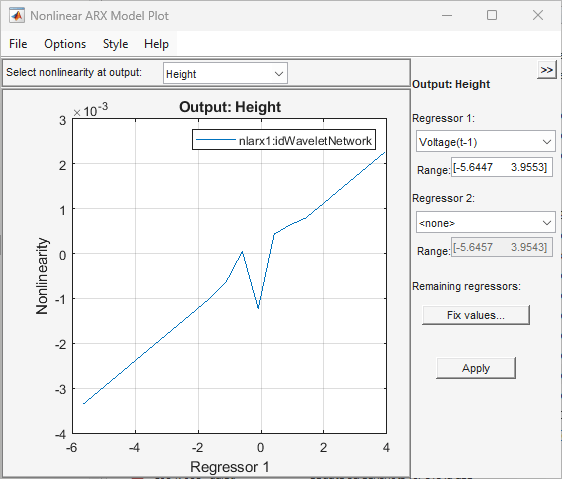
Modifier une structure de modèle non linéaire
Dans cette partie du tutoriel, vous estimez un modèle ARX non linéaire avec un retard d’entrée et des paramètres de non-linéarité spécifiques. Généralement, vous sélectionnez des ordres de modèle en méthode essai-erreur jusqu’à obtenir un modèle qui produit un ajustement précis aux données.
Vous devez avoir déjà estimé le modèle ARX non linéaire avec des paramètres par défaut, comme décrit dans Estimer un modèle ARX non linéaire avec des paramètres par défaut.
Dans la boîte de dialogue Estimate Nonlinear ARX Models, sélectionnez l’onglet Model Structure, puis sélectionnez l’onglet Regressors.
Dans le panneau Configure: Linear regressors #1, remplacez les décalages de la variable
Voltagepar[3 4]. En effet, les données suggèrent qu’il y a au minimum 3 échantillons de décalage entre l’entrée et la sortie.Cette action met à jour la liste des variables explicatives pour afficher les termes
Voltage(t-3)etVoltage(t-4)avec un retard minimum de trois échantillons.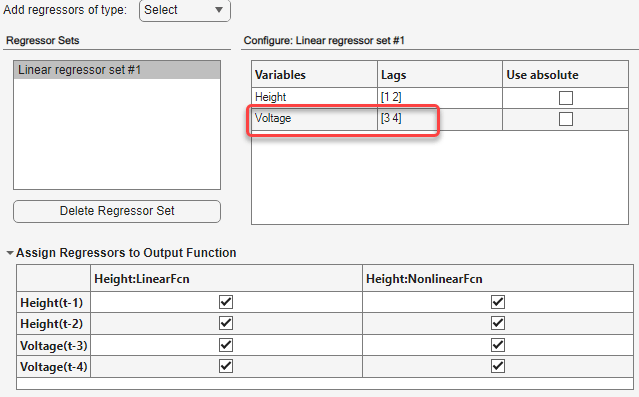
Cliquez sur Estimate.
Cette action ajoute le modèle
nlarx2à l’application System Identification et met à jour la fenêtre Model Output pour inclure ce modèle. Double-cliquez sur l’icônenlarx2dans le tableau des modèles de la fenêtre principale de l’application pour afficher les résultats de l’estimation.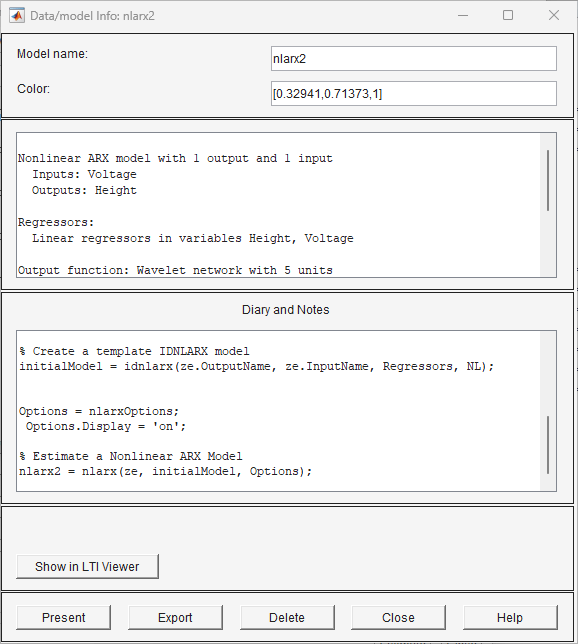
L’application met également à jour le tracé de la sortie du modèle pour afficher l’ajustement du modèle
nlarx2au jeu de données de validationzv. Le graphique montre que le choix de décalages corrects pour les variables d’entrée améliore l’ajustement.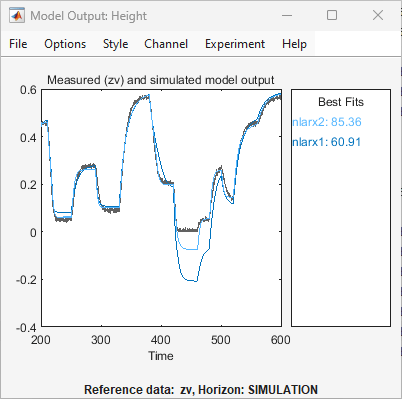
Dans la boîte de dialogue Estimate Nonlinear ARX Models, sélectionnez l’onglet Model Structure, puis sélectionnez l’onglet Output Function.
Pour Number of Units, sélectionnez Enter et saisissez
6. La définition d’un nombre spécifique contrôle la flexibilité de la fonction non linéaire en spécifiant directement le nombre d’ondelettes utilisé par Wavelet Network.
Cliquez sur Estimate.
Cette action ajoute le modèle
nlarx3à l’application System Identification. Elle met également à jour la fenêtre Model Output, comme le montre la figure suivante.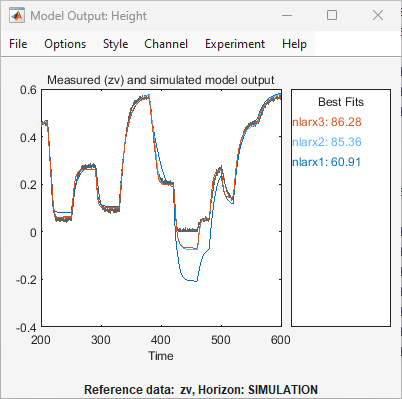
Utiliser des variables explicatives polynomiales
Vous pouvez estimer un modèle ARX non linéaire qui utilise des puissances supérieures de variables décalées comme variables explicatives. Dans cet exemple, vous ajoutez des polynômes de second ordre de variables décalées, y compris des termes croisés.
Dans la boîte de dialogue Estimate Nonlinear ARX Models, sélectionnez l’onglet Model Structure, puis sélectionnez l’onglet Regressors.
Développez Add regressors of type et sélectionnez Polynomial.
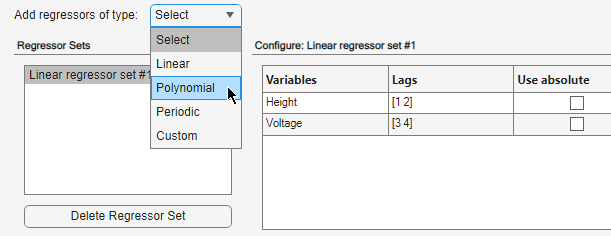
Cette action ajoute un jeu de variables explicatives polynomiales, appelées
Polynomial regressors #1, à la liste des jeux de variables explicatives. Par défaut, ce jeu est configuré pour générer des variables explicatives d’ordre polynomial deux.Remplacez les décalages de
Voltagepar[3 4].Sélectionnez Mix lags pour inclure tous les termes croisés. Cette action ajoute dix variables explicatives de second ordre au modèle, en plus des quatre apportées par Linear regressor #1.
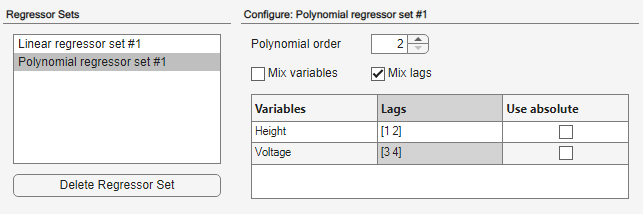
Cliquez sur Estimate. Cette action ajoute le modèle
nlarx4à l’application. L’application met à jour le graphique Model Output, comme le montre la figure suivante.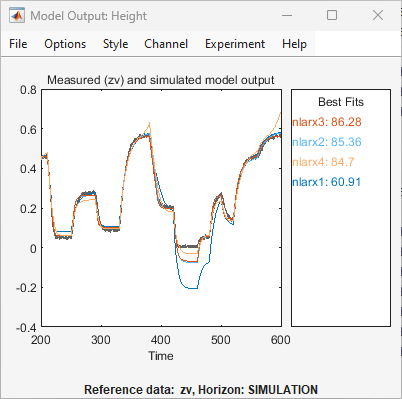
Le graphique montre que l’ajout de variables explicatives polynomiales n’a pas amélioré la capacité de généralisation du modèle. Autrement dit, le modèle ne fournit pas un meilleur ajustement entre la sortie du modèle et la sortie mesurée pour des données de validation indépendantes. Ce résultat est un scénario avec surajustements (overfits) typique, c’est-à-dire que le modèle contient plus de variables explicatives qu’absolument nécessaire.
Sélectionner un sous-ensemble de variables explicatives dans un bloc non linéaire
Vous pouvez estimer un modèle ARX non linéaire qui inclut uniquement un sous-ensemble de variables explicatives en entrée du bloc non linéaire. Par défaut, toutes les variables explicatives sont utilisées dans le bloc non linéaire. Dans cette partie du tutoriel, vous attribuez uniquement un sous-ensemble de variables explicatives au bloc non linéaire.
Vous devez avoir déjà spécifié la structure de modèle, comme décrit dans Modifier une structure de modèle non linéaire.
Dans la boîte de dialogue Estimate Nonlinear ARX Models, sélectionnez l’onglet Model Structure, puis sélectionnez l’onglet Regressors.
S’il est réduit, développez le panneau Assign Regressors to Output Function.
Effacez les sélections de toutes les variables explicatives de second ordre dans la colonne Height:NonlinearFcn de la table. Effacez également les sélections de toutes les variables explicatives avec des termes croisés (c’est-à-dire des variables explicatives composées de produits de 2 termes) de Height:LinearFcn.

Cliquez sur Estimate.
Cette action ajoute le modèle
nlarx5à l’application System Identification. Elle met également à jour la fenêtre Model Output.
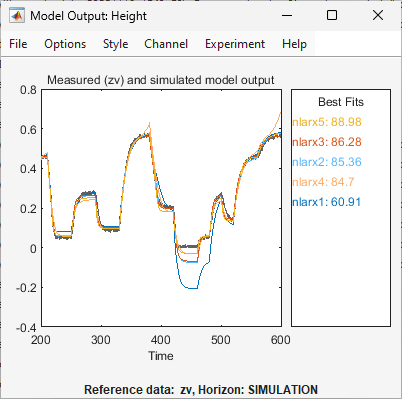
Ce modèle montre une meilleure capacité de généralisation.
Spécifier un modèle estimé précédemment avec une non-linéarité différente dans la fonction de sortie
Vous pouvez estimer une suite de modèles ARX non linéaires par variations systématiques de la structure de modèle et baser chaque nouveau modèle sur la configuration d’un modèle estimé précédemment. Dans cette partie du tutoriel, vous estimez un modèle ARX non linéaire similaire à un modèle existant (nlarx3), mais avec une non-linéarité différente dans la fonction de sortie.
Dans la boîte de dialogue Estimate Nonlinear ARX Models, sélectionnez l’onglet Model Structure.
Cliquez sur Select à côté de Initialize using existing model (optional). Dans la boîte de dialogue Initialize Model, sélectionnez l’onglet
nlarx3dans Nonlinear model et cliquez sur OK. Cette action règle les propriétés qui sont affichées dans les onglets Regressors et Output Function sur les valeurs correspondant ànlarx3.
Sélectionnez l’onglet Output Function.
Dans la table, changez le choix de Nonlinear Function, en
Sigmoid Network. Cette action règle la fonction de sortie sur un réseau sigmoïde.Dans Enter the number of units, saisissez
6.
Cliquez sur Estimate.
Cette action ajoute le modèle
nlarx6à l’application System Identification. Elle met également à jour le graphique Model Output, comme le montre la figure suivante.
Sélectionner le meilleur modèle
Le meilleur modèle est le modèle le plus simple qui décrit avec précision la dynamique. Les résultats indiquent que le modèle nlarx3 est susceptible d’être le meilleur modèle idnlarx pour ces données, d’après les différentes structures de modèle examinées dans cet exemple.
Exporter le meilleur modèle dans l’espace de travail de base
Faites glisser l’icône nlarx3 dans la case To Workspace de la fenêtre principale de l’application System Identification. Autrement, double-cliquez sur l’icône nlarx3 pour ouvrir son tableau d’information. Cliquez alors sur Export pour exporter le modèle dans l’espace de travail.

Estimer des modèles de Hammerstein-Wiener
Estimer des modèles de Hammerstein-Wiener avec des paramètres par défaut
Dans cette partie du tutoriel, vous estimez un modèle de Hammerstein-Wiener non linéaire à l’aide d’une structure de modèle par défaut et d’options d’estimation.
Vous devez avoir déjà préparé les données, comme décrit dans Préparation des données. Pour plus d'informations sur les modèles ARX non linéaires, consultez Qu'est-ce qu'un modèle de Hammerstein-Wiener ?.
Remarque
Les illustrations de ce tutoriel représentent une session typique de l’application System Identification. Vos résultats peuvent ne pas correspondre exactement aux résultats sur les images.
Dans l’application System Identification, sélectionnez Estimate > Hammerstein-Wiener Models pour ouvrir la boîte de dialogue Estimate Hammerstein-Wiener Models. La boîte de dialogue contient deux onglets : Model Structure et Estimation Options.
Inspection de la structure de modèle par défaut. L’onglet Model Structure contient trois onglets, un pour chaque composante du modèle. Ces composantes sont la non-linéarité d’entrée, le bloc dynamique linéaire et la non-linéarité de sortie.
Sélectionnez l’onglet Input Nonlinearity. La non-linéarité par défaut est une fonction Piecewise Linear avec 10 points de coupure.

Sélectionnez l’onglet Linear Block. La fonction de transfert linéaire a un ordre de numérateur égal à 2, ce qui implique un polynôme de second ordre dans z-1, un ordre de dénominateur égal à 3 et un retard d’entrée de 1 échantillon.

Sélectionnez l’onglet Output Nonlinearity. Comme pour l’onglet Input Nonlinearity, la non-linéarité par défaut est une fonction Piecewise Linear avec 10 points de coupure.

Cliquez sur Estimate.
Cette action estime les paramètres du modèle de Hammerstein-Wiener afin de minimiser la différence entre la sortie du modèle et la sortie mesurée (
ze.OutputData). Les paramètres estimés sont :Les emplacements des points de coupure (coordonnées x et y) des fonctions linéaires par morceaux d’entrée et de sortie.
Les coefficients polynomiaux du numérateur et du dénominateur qui composent la fonction de transfert du bloc linéaire.
Le software ajoute le modèle estimé
nlhw1au tableau des modèles de l’application System Identification.
Dans l’application System Identification, sélectionnez la case à cocher Model output.
Cette action simule le modèle à l’aide des données de validation d’entrée comme entrée du modèle et trace la sortie simulée au-dessus des données de validation de sortie. Notez que les données de validation sont définies par
zv.
La zone Best Fits de la fenêtre Model Output montre la correspondance entre la sortie du modèle et la sortie des données de validation.

La validité du modèle
nlhw1n’est pas très bonne. L’ajustement àzv.OutputDataest médiocre.
Tracer des non-linéarités et la fonction de transfert non linéaire
Vous pouvez tracer les non-linéarités d’entrée/sortie et la fonction de transfert linéaire du modèle sur un tracé de Hammerstein-Wiener.
Dans l’application System Identification, sélectionnez Hamm-Wiener pour visualiser le tracé du modèle de Hammerstein-Wiener.
Le tracé affiche la non-linéarité d’entrée, comme le montre la figure suivante.

Cliquez sur le rectangle yNL dans la partie supérieure de la fenêtre Hammerstein-Wiener Model Plot.
Le tracé se met à jour et affiche la non-linéarité de sortie.

Cliquez sur le rectangle Linear Block dans la partie supérieure de la fenêtre Hammerstein-Wiener Model Plot.
Le graphique se met à jour et affiche la réponse indicielle de la fonction de transfert linéaire.

Dans la liste Choose plot type, sélectionnez
Bode. Cette action affiche le diagramme de Bode de la fonction de transfert linéaire.
Modifier le retard en entrée du modèle de Hammerstein-Wiener
Dans cette partie du tutoriel, vous estimez un modèle de Hammerstein-Wiener avec un ordre de modèle et des paramètres de non-linéarité spécifiques. Généralement, vous sélectionnez des ordres de modèle et des retards avec une méthode d'essai-erreur jusqu’à obtenir un modèle qui produit un ajustement satisfaisant aux données.
Vous devez avoir déjà estimé le modèle de Hammerstein-Wiener avec des paramètres par défaut, comme décrit dans Estimer des modèles de Hammerstein-Wiener avec des paramètres par défaut.
Dans la boîte de dialogue Estimate Hammerstein-Wiener, sélectionnez l’onglet Model Structure, puis l’onglet Linear Block.
Pour le canal d’entrée
Voltage, double-cliquez sur la cellule Input Delay (nk) correspondante et saisissez la valeur3.Cliquez sur Estimate.
Cette action ajoute le modèle
nlhw2à l’application System Identification et met à jour le graphique Model Output, comme le montre la figure suivante.
Le panneau Best Fits de la fenêtre Model Output montre la qualité de l’ajustement
nlhw2, qui est meilleur que celui du modèlenlhw1.
Modifier l’estimateur de non-linéarité dans un modèle de Hammerstein-Wiener
Dans cette partie de l’exemple, vous modifiez la structure du modèle de Hammerstein-Wiener par défaut en changeant son estimateur de non-linéarité.
Conseil
Si vous savez que votre système inclut des non-linéarités de saturation ou de zone morte, vous pouvez spécifier ces estimateurs de non-linéarité spécifiques dans votre modèle. Piecewise Linear, Wavelet Network et Sigmoid Network sont des estimateurs de non-linéarité pour une approximation de non-linéarité générale.
Dans la boîte de dialogue Estimate Hammerstein-Wiener Models, sélectionnez l’onglet Model Structure, puis l’onglet Input Nonlinearity.
Cliquez sur la cellule Nonlinearity de la variable
Voltageet sélectionnezSigmoid Networkdans la liste.
Dans Enter the number of units, réglez la valeur sur
20.
Cliquez sur Estimate.
Cette action ajoute le modèle
nlhw3à l’application System Identification. Elle met également à jour la fenêtre Model Output, comme le montre la figure suivante.
Dans la boîte de dialogue Estimate Hammerstein-Wiener Models, sélectionnez l’onglet Input Nonlinearity.
Pour l’entrée
Voltage, réglez Nonlinearity surWavelet Network. La valeur par défaut de Number of Units est Select Automatically.
Sélectionnez l’onglet Output Nonlinearity.
Réglez la sortie
HeightNonlinearity surOne-dimensional Polynomial. Réglez Degree of polynomial sur2.
Cliquez sur Estimate.
Cette action ajoute le modèle
nlhw4à l’application System Identification. Elle met également à jour la fenêtre Model Output, comme le montre la figure suivante.
Sélectionner le meilleur modèle
Le meilleur modèle est le modèle le plus simple qui décrit avec précision la dynamique.
Dans cet exemple, les modèles nlhw3 et nlhw4 sont de bons candidats.