La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Estimer un modèle de processus

Estimer un modèle de processus en temps continu pour un système à entrée unique et à sortie unique (SISO) dans le domaine temporel ou fréquentiel dans le Live Editor

Description

La tâche Estimate Process Model (Estimer un modèle de processus) vous permet d’estimer et de valider interactivement un modèle de processus pour les systèmes SISO. Vous pouvez définir et faire varier la structure du modèle et spécifier des paramètres optionnels tels que le traitement des conditions initiales et les méthodes de recherche. La tâche génère automatiquement un code MATLAB^® pour votre live script. Pour plus d’informations sur les tâches du Live Editor en général, consultez Add Interactive Tasks to a Live Script.

Les modèles de processus sont de simples fonctions de transfert en temps continu qui décrivent la dynamique de système linéaire. Les éléments de modèle de processus comprennent le gain statique, les constantes de temps, les retards de temps, l’intégrateur et le zéro de processus.

Les modèles de processus sont populaires lorsqu’il s’agit de décrire la dynamique des systèmes dans de nombreux secteurs. Ils peuvent s’appliquer à divers environnements de production. Ces modèles ont pour avantages d’être simples et de prendre en charge l’estimation des retards de transport. En outre, les coefficients du modèle sont faciles à interpréter en tant que pôles et zéros. Pour plus d’informations sur l’estimation d’un modèle de processus, consultez What Is a Process Model?

La tâche Estimate Process Model est indépendante de l’application System Identification plus générale. Utilisez l’application System Identification quand vous voulez calculer et comparer des estimations pour plusieurs structures de modèle.

Pour démarrer, chargez des données expérimentales contenant des données d’entrée et de sortie sur votre espace de travail MATLAB, puis importez ces données dans la tâche. Sélectionnez ensuite une structure de modèle à estimer. La tâche vous donne des contrôles et des tracés que vous pouvez expérimenter avec différentes structures de modèle afin de comparer la qualité de l’ajustement de la sortie de chaque modèle aux mesures.

Fonctions connexes

Le code généré par Estimate Process Model utilise les fonctions suivantes.

• iddata

• idfrd

  frd (Control System Toolbox)

• procest

• procestOptions

• compare

La tâche estime un modèle de processus idproc.

Ouvrir la tâche

Pour ajouter la tâche Estimate Process Model à un live script dans MATLAB Editor :

• Dans l’onglet Live Editor, sélectionnez Task > Estimate Process Model.

• Dans un bloc de code de votre script, tapez un mot clé utile, tel que process ou estimate. Sélectionnez Estimate Process Model parmi les complétions de commande suggérées.

Exemples

Estimer un modèle de processus avec la tâche Live Editor

Utilisez la tâche Live Editor Estimate Process Model pour estimer un modèle de processus et comparer la sortie du modèle aux données de mesure.

Configurer des données

Chargez les données de mesure tt1 sur votre espace de travail MATLAB. tt1 est une timetable qui contient une variable d’entrée u et une variable de sortie y.

load sdata1 tt1

Importer les données dans la tâche

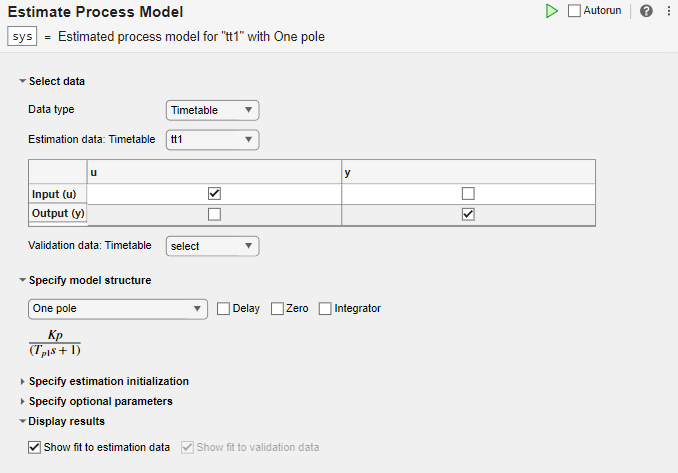
Dans la section Select data, définissez le Data type sur Timetable et définissez Estimation data sur tt1.

La tâche affiche un tableau contenant les noms de variables d’entrée et de sortie tt1.

Estimer le modèle avec les paramètres par défaut

Examinez la structure du modèle et les paramètres optionnels.

Dans la section Specify model structure, l’option par défaut est One Pole sans délai, zéro ou intégrateur. Les équations sous les paramètres de cette section affichent la structure spécifiée.

Dans la section Specify estimation initialization, les paramètres d’initialisation correspondant aux paramètres de votre structure de modèle vous permettent de définir des points de départ pour l’estimation. Si vous sélectionnez Fix, le paramètre reste fixé à la valeur que vous spécifiez. Pour cet exemple, ne spécifiez pas d’initialisation. La tâche utilise donc des valeurs par défaut pour les points de départ.

Dans la section Specify optional parameters, les options par défaut pour l’estimation de processus sont définies.

Exécutez la tâche depuis l’onglet Live Editor en cliquant sur la flèche verte. Vous pouvez également sélectionner Autorun pour exécuter la tâche automatiquement à chaque fois que vous mettez à jour un paramètre.

Un tracé affiche les données d’estimation, la sortie du modèle estimée et le pourcentage d’ajustement.

Expérimenter avec différentes configuration de paramètres

Expérimentez avec différentes configurations de paramètres et observez comment cela influe sur l’ajustement.

Par exemple, ajoutez un retard à la structure One Pole et exécutez la tâche.

L’ajustement d’estimation s’améliore, bien que le pourcentage d’ajustement reste sous 50 %.

Essayez une structure de modèle différente. Dans Specify model structure, sélectionnez Underdamped Pair sans retard et exécutez la tâche.

Les résultats d’ajustement s’améliorent considérablement.

Générer le code

Pour afficher le code généré par la tâche, cliquez sur au bas de la section des paramètres. Le code que vous voyez montre la configuration actuelle des paramètres de la tâche.

Utiliser un jeu de données de validation pour valider un modèle estimé

Utilisez des données d’estimation et de validation séparées afin que vous puissiez valider le modèle de processus estimé.

Configurer des données

Chargez les données de mesure sdata1 sur votre espace de travail MATLAB et examinez leur contenu.

load sdata1 umat1 ymat1 Ts

Divisez les données en deux jeux, une moitié pour l’estimation et l’autre pour la validation. Le jeu de données original avait 300 échantillons, donc chaque nouveau jeu de données doit avoir 150 échantillons.

u_est = umat1(1:150);
u_val = umat1(151:300);
y_est = ymat1(1:150);
y_val = ymat1(151:300);
Ts

Ts = 
0.1000

Importer les données dans la tâche

Dans la section Select data, définissez le Data type sur « Numeric ». Spécifiez le pas d’échantillonnage sur 0.1 seconde. Sélectionnez les jeux de données appropriés pour l’estimation et la validation.

Estimer et valider le modèle

L’exemple Estimer un modèle de processus avec la tâche Live Editor obtient les meilleurs résultats avec la structure de modèle Underdamped Pair. Choisissez la même option pour cet exemple.

Exécutez la tâche. Exécuter la tâche crée deux tracés. Le premier tracé montre les résultats d’estimation et le deuxième tracé montre les résultats de validation.

L’ajustement aux données d’estimation est un peu moins bon que dans Estimer un modèle de processus avec la tâche Live Editor. L’estimation dans cet exemple ne possède que la moitié des données avec lesquelles estimer le modèle. L’ajustement aux données de validation, qui représente la qualité du modèle plus généralement, est meilleur que l’ajustement aux données d’estimation.

Paramètres

Sélectionner les données

Data Type — Type de données pour les données d’entrée et de sortie

Numeric (par défaut) | Timetable | Frequency | Data Object

La tâche accepte des valeurs de mesure numériques qui sont échantillonnées uniformément dans le temps. Les signaux numériques d’entrée et de sortie peuvent contenir plusieurs canaux. Les données peuvent être packagées en tant que tableaux numériques (pour Numeric ou Frequency), timetable ou objet de données, tel qu’un objet iddata ou idfrd. Pour les données multi-expérimentations, les données numériques et de timetable peuvent être packagées en tant que cell arrays. Pour les cell arrays de timetables, toutes les timetables doivent contenir les mêmes noms de variable. Les objets de données gèrent les données multi-expérimentations en interne.

Le type de données que vous choisissez détermine si vous devez spécifier des paramètres supplémentaires.

• Numeric — Spécifiez Sample Time et Start Time dans les unités de temps que vous sélectionnez.

• Timetable — Ne spécifiez aucun paramètre supplémentaire parce que la timetable contient déjà des informations sur le pas d’échantillonnage et l’heure de début.

• Frequency — Spécifiez Frequency en sélectionnant le nom de la variable d’un vecteur de fréquence dans votre espace de travail MATLAB. Spécifiez les unités pour ce vecteur de fréquence. Spécifiez Sample Time en secondes.

• Data Object — Ne spécifiez aucun paramètre supplémentaire parce que l’objet de données contient déjà des informations sur le temps ou la fréquence d’échantillonnage.

Estimation and Validation data: Input (u) and Output (y) — Noms de variable des données d’entrée et de sortie pour l’estimation ou la validation

noms de variable valides

Sélectionnez les noms de variables d’entrée et de sortie parmi les choix de l’espace de travail MATLAB. Utilisez ces paramètres quand Data Type est Numeric ou Frequency.

Spécifier les données de validation est optionnel, mais recommandé.

Estimation and Validation data: Timetable — Nom de variable d’une timetable à utiliser pour l’estimation ou la validation

nom de variable valide

Sélectionnez le nom de variable de timetable parmi les choix de l’espace de travail MATLAB. Utilisez ce paramètre quand Data Type est Timetable. La tâche affiche les noms de variable de timetable pour l’entrée et la sortie. Les timetables d’estimation et de validation doivent contenir les mêmes noms de variable.

Estimation and Validation Data Object — Nom de variable d’un objet de données (objet iddata, idfrd ou frd) contenant des données d’entrée et de sortie à utiliser pour l’estimation ou la validation

nom de variable valide

Sélectionnez le nom de variable de l’objet de données parmi les choix de l’espace de travail MATLAB. Utilisez ce paramètre quand Data Type est Data Object.

Spécifier une structure de modèle

Structure — Pôles et zéros d’un modèle

One Pole (par défaut) | Two Real Poles | Underdamped Pair | Underdamped Pair + Real Pole

La tâche vous permet de spécifier l’une des quatre structures de base. Ces structures vont d’un processus de premier ordre simple à un processus de deuxième ordre ou de troisième ordre, avec des pôles (sous-amortis) conjugués complexes.

• One Pole

• Two Real Poles

• Underdamped Pair

• Underdamped Pair + Real Pole

Delay — Inclure le retard de transport

off (par défaut) | on

Inclure le retard de transport, ou le retard entre l’entrée et la sortie, d’un échantillon. Le retard de transport est aussi appelé temps mort.

Zero — Inclure le zéro de processus

off (par défaut) | on

Inclure un zéro de processus dans le numérateur.

Integrator — Inclure l’intégrateur

off (par défaut) | on

Inclure un intégrateur, représenté par un terme 1/ s supplémentaire. Inclure un intégrateur crée un processus autorégulateur.

Spécification de l’initialisation de l’estimation

Initial Values — Valeurs initiales des paramètres de structure

0 | valeurs de paramètres

Spécifiez des valeurs initiales pour l’estimation et si ces valeurs doivent être fixes ou estimées. Les valeurs à spécifier dépendent de la structure du modèle et de vos spécifications pour Delay et Zero. Sous Specify model structure, la tâche affiche l’équation qui représente le système spécifié. Cette équation contient tous les paramètres qui peuvent être estimés et que vous pouvez initialiser ou fixer. Les paramètres possibles sont :

• Kp — Gain statique

• T_p1 — Constante de temps pour le premier pôle réel

• T_p2 — Constante de temps pour le deuxième pôle réel

• Tω — Constante de temps pour les pôles complexes, égale à l’inverse de la fréquence naturelle

• ζ — Coefficient d’amortissement pour les pôles complexes

• T_d : retard de transport

• T_z — Constante de temps pour le zéro de processus

Tous les paramètres basés sur le temps sont dans les unités de temps que vous sélectionnez pour Sample Time.

Spécifier des paramètres optionnels

Fit Focus — Minimiser l’erreur de prédiction ou l’erreur de simulation

Prediction (par défaut) | Simulation

Le « Fit focus » spécifie quelle erreur doit être minimisée dans la fonction de perte pendant l’estimation.

• Prediction — Minimise l’erreur de prédiction un pas avant entre les sorties mesurées et prédites. Cette approche d’estimation se concentre sur la production d’un bon modèle de prédiction pour les entrées et les sorties d’estimation. Le focus de prédiction produit en général les meilleurs résultats d’estimation car il utilise aussi bien les mesures d’entrée que de sortie, ce qui lui permet donc de prendre en compte les perturbations.

• Simulation — Minimise l’erreur entre les sorties mesurées et de simulation. Cette approche d’estimation se concentre sur la production d’une réponse du modèle simulée qui a un bon ajustement avec les entrées et les sorties d’estimation. Le focus de simulation est en général meilleur pour la validation, en particulier avec les jeux de données qui n’ont pas été utilisés pour l’estimation originale.

Initial Conditions — Traitement des conditions initiales

Auto (par défaut) | Zero | Estimate | Backcast

Définissez cette option quand vous souhaitez choisir une méthode spécifique pour initialiser le modèle. Avec le paramètre par défaut de Auto, le logiciel choisit la méthode en fonction des données d’estimation. Les choix sont les suivants :

• Zero — L’état initial est défini sur zéro.

• Estimate — L’état initial est traité comme un paramètre d’estimation indépendant.

• Backcast — L’état initial est estimé à l’aide du meilleur ajustement des moindres carrés.

Input Intersampling — Comportement entre les échantillons pour un signal d’entrée

Zero-order hold (par défaut) | Triangle approximation | Band-limited

Le comportement des entrées entre les échantillons est une propriété des données d’entrée. La tâche utilise cette propriété lors de l’estimation de modèles de processus. Spécifiez Input Intersampling quand votre type de données est Time ou Frequency. Si vous utilisez un objet iddata, l’objet contient déjà les informations entre les échantillons. Les choix pour cette propriété sont les suivants :

• Zero-order hold — Signal d’entrée constant par morceaux entre échantillons

• Triangle approximation — Signal d’entrée linéaire par morceaux entre échantillons, aussi appelé bloqueur de premier ordre

• Band-limited — Le signal d’entrée n’a aucune puissance au-dessus de la fréquence de Nyquist

Search Method — Mode de recherche numérique pour l’estimation des paramètres itérative

Auto (par défaut) | Gauss-Newton | Adaptive Gauss-Newton | Levenberg-Marquardt | Gradient search | Trust-Region Reflective Newton | Pattern Search | Sequential Quadratic Programming (SQP) | Interior-Point

Les méthodes de recherche numériques pour l’estimation itérative des paramètres sont les suivantes :

Méthode de recherche	Description
Auto	Pour chaque itération, le logiciel parcourt les méthodes jusqu’à ce qu’il trouve la première direction de descente parvenant à une réduction du coût estimé.
Gauss-Newton	Les valeurs singulières de la matrice jacobienne inférieures à GnPinvConstant*eps*max(size(J))*norm(J) sont écartées lors du calcul de la direction de recherche. J est la matrice jacobienne. La matrice hessienne est estimée sous la forme de JTJ. Si cette direction ne montre aucune amélioration, la fonction essaie la direction de gradient.
Adaptive Gauss-Newton	Les valeurs propres inférieures à gamma*max(sv) de la matrice hessienne sont ignorées, où sv contient les valeurs singulières de la matrice hessienne. La direction de Gauss-Newton est calculée dans le sous-espace restant. gamma a pour valeur initiale InitialGnaTolerance (consultez Advanced dans 'SearchOptions' pour plus d’informations). Cette valeur augmente du facteur LMStep à chaque fois que la recherche ne parvient pas à trouver une valeur inférieure du critère en moins de cinq bissections. Cette valeur diminue du facteur 2*LMStep à chaque fois qu’une recherche réussit sans aucune bissection.
Levenberg-Marquardt	Chaque valeur de paramètre est -pinv(H+d*I)*grad par rapport à la valeur précédente. H est la matrice hessienne, I est la matrice identité et grad est le gradient. d est un nombre qui augmente jusqu’à ce qu’une valeur inférieure du critère soit trouvée. Cette méthode nécessite le logiciel Optimization Toolbox™. Pour plus d’informations, consultez Levenberg-Marquardt Method (Optimization Toolbox).
Gradient search	Recherche des moindres carrés avec la descente la plus forte.
Trust-Region Reflective Newton	Un solveur non linéaire contraint. Ce solveur nécessite le logiciel Optimization Toolbox. Pour plus d’informations, consultez fmincon Trust Region Reflective Algorithm (Optimization Toolbox).
Pattern Search	Solveur pour des non-linéarités sans gradients bien définis. Ce solveur nécessite le logiciel Global Optimization Toolbox. Pour plus d’informations, consultez patternsearch (Global Optimization Toolbox).
Sequential Quadratic Programming (SQP)	Un solveur non linéaire contraint. Ce solveur nécessite le logiciel Optimization Toolbox. Pour plus d’informations, consultez fmincon SQP Algorithm (Optimization Toolbox).
Interior-Point	Un solveur non linéaire contraint. Ce solveur nécessite le logiciel Optimization Toolbox. Pour plus d’informations, consultez fmincon Interior Point Algorithm (Optimization Toolbox).

Max. Iterations — Nombre maximum d’itérations pendant la minimisation d’erreurs

20 (par défaut) | entier positif

Définissez le nombre maximum d’itérations pendant la minimisation d’erreurs. Les itérations s’arrêtent quand Max. Iterations est atteint ou qu’un autre critère d’arrêt est respecté, tel que Tolerance.

Tolerance — Pourcentage minimum d’amélioration d’erreur attendue

0.01 (par défaut) | entier positif

Quand le pourcentage d’amélioration attendue est inférieur à Tolerance, les itérations s’arrêtent.

Weighting Prefilter — Préfiltre de pondération pour la fonction de perte

No filter (par défaut) | Passband(s) | LTI Filter | Frequency weights vector

Définissez cette option quand vous souhaitez appliquer un préfiltre de pondération à la fonction de perte que la tâche minimise quand vous estimez le modèle. Quand vous sélectionnez une option, vous devez également sélectionner la variable associée qui contient les informations de filtre dans votre espace de travail. Les options disponibles dépendent du domaine des données.

Préfiltre de pondération	Domaine des données	Informations sur les filtres
No Filter	Temporel et fréquentiel
Passbands	Temporel et fréquentiel	Plages de bandes passantes, spécifiées comme vecteur ligne de 1 par 2 ou matrice de n par 2, où n est le nombre de bandes passantes
LTI Filter	Temporel et fréquentiel	Modèle LTI SISO
Frequency Weights Vector	Fréquentiel	Poids de fréquence, spécifiés comme vecteur colonne de même longueur que le vecteur de fréquence

Par exemple, supposons que vous effectuez une estimation avec des données dans le domaine fréquentiel SISO et que dans votre espace de travail MATLAB vous avez un vecteur colonne W qui contient les poids de fréquence pour le préfiltre. Dans la tâche, sélectionnez Weighting prefilter > Frequency weights vector et la variable W.

Visualiser les résultats

Output Plot — Tracer la comparaison des sorties de modèle et des sorties mesurées

on (par défaut) | off

Tracez une comparaison de la sortie du modèle et des données mesurées originales, ainsi que du pourcentage d’ajustement. Si vous avez des données de validation séparées, un deuxième tracé compare la réponse du modèle aux données d’entrée de validation avec la sortie mesurée à partir du jeu de données de validation.

Historique des versions

Introduit dans R2019b

R2025a: Nouveau solveur de recherche de patterns disponible pour l’estimation

Vous pouvez maintenant estimer un système qui a une non-linéarité sans un gradient bien défini, en choisissant la Search Method comme Pattern Search. Cette méthode nécessite le logiciel Global Optimization Toolbox.

R2024b: Prise en charge des données multi-expérimentations

La tâche Live Editor Estimate Process Model supporte maintenant les données multi-expérimentations.

R2023b: Données d’estimation basées sur une timetable acceptées

La tâche est mise à jour pour accepter des données dans le domaine temporel sous la forme d’une timetable. La tâche continue d’accepter des données numériques dans le domaine temporel également, avec l’option de type de données Numeric.

Voir aussi

timetable | iddata | procest | procestOptions | compare | idproc | idfrd | frd (Control System Toolbox)