Tailles de tableau compatibles pour les opérations de base

La plupart des opérateurs et des fonctions binaires (à deux entrées) de MATLAB® supportent les tableaux numériques de tailles compatibles. Deux entrées sont de tailles compatibles si, pour chaque dimension, les tailles de dimension des entrées sont les mêmes ou si l’une d’entre elles est 1. Dans les cas les plus simples, deux tailles de tableau sont compatibles si elles sont exactement les mêmes ou si l’une est un scalaire. MATLAB étend implicitement les tableaux de tailles compatibles pour qu’ils soient de la même taille pendant l’exécution de l’opération ou de la fonction élément par élément.

Entrées de tailles compatibles

Entrées 2D

Voici quelques combinaisons de scalaires, de vecteurs et de matrices de tailles compatibles :

  • Deux entrées qui sont exactement de la même taille.

    If A and B are the same size, then the result has the same size.

  • Une entrée est un scalaire.

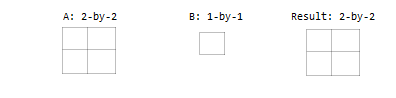
    If A is a matrix and B is a scalar, then the result is the same size as A.

  • Une entrée est une matrice et l’autre est un vecteur colonne comportant le même nombre de lignes.

    If A is 4-by-2 and B is 4-by-1, then the result is 4-by-2.

  • Une entrée est un vecteur colonne et l’autre est un vecteur ligne.

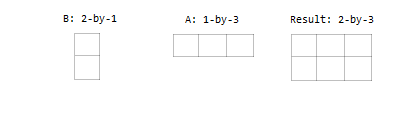
    If B is 2-by-1 and A is 1-by-3, then the result is 2-by-3.

Tableaux multidimensionnels

Chaque tableau de MATLAB comporte des dimensions finales de taille 1. Pour les tableaux multidimensionnels, cela signifie qu’une matrice de 3 par 4 est identique à une matrice de taille 3 par 4 par 1 par 1 par 1. Voici quelques exemples de tableaux multidimensionnels de tailles compatibles :

  • Une entrée est une matrice et l’autre est un tableau 3D comportant le même nombre de lignes et de colonnes.

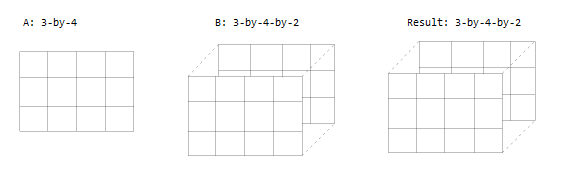
    If A is 3-by-4 and B is 3-by-4-by-2, then the result is 3-by-4-by-2.

  • Une entrée est une matrice et l’autre est un tableau 3D. Les dimensions sont soit toutes les mêmes, soit l’une d’entre elles est 1.

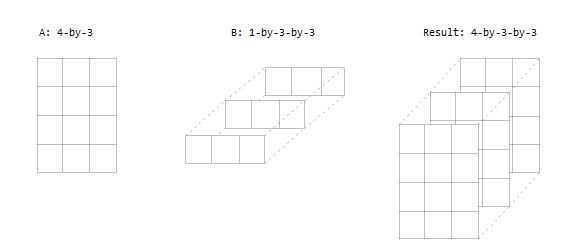
    If A is 4-by-3 and B is 1-by-3-by-3, then the result is 4-by-3-by-3.

Tableaux vides

Les règles sont les mêmes pour les tableaux vides ou les tableaux qui ont une taille de dimension de zéro. La taille de la dimension qui n’est pas égale à 1 détermine la taille de la sortie. Ceci signifie que les dimensions de taille zéro doivent être associées à une dimension de taille 1 ou 0 dans l’autre tableau et que la sortie a une taille de dimension de 0.

     A: 1-by-0     
     B: 3-by-1
Result: 3-by-0

Entrées de tailles incompatibles

Les entrées incompatibles sont de tailles qui ne peuvent pas être étendues implicitement pour être de même taille. Par exemple :

  • Une des tailles de dimensions n’est pas égale aux autres et n’est pas 1 non plus.

    A: 3-by-2
B: 4-by-2

  • Deux vecteurs ligne non scalaires de longueurs différentes.

    A: 1-by-3
B: 1-by-4

Exemples

Soustraire un vecteur d’une matrice

Pour simplifier les opérations vecteur-matrice, utilisez l’expansion implicite avec des fonctions dimensionnelles telles que sum, mean, min, entre autres.

Par exemple, calculez la valeur moyenne de chaque colonne d’une matrice, puis soustrayez la valeur moyenne de chaque élément.

A = magic(3)
A =

     8     1     6
     3     5     7
     4     9     2
C = mean(A)
C =

     5     5     5
A - C
ans =

     3    -4     1
    -2     0     2
    -1     4    -3

Ajouter un vecteur ligne ou un vecteur colonne

Les vecteurs ligne et les vecteurs colonne sont de tailles compatibles, et quand vous effectuez une opération sur eux, le résultat est une matrice.

Par exemple, ajoutez un vecteur ligne et un vecteur colonne. Le résultat est identique à bsxfun(@plus,a,b).

a = [1 2 3 4]

ans =

     1     2     3     4
b = [5; 6; 7]
ans =

     5
     6
     7
a + b
ans =

     6     7     8     9
     7     8     9    10
     8     9    10    11

Voir aussi

Rubriques