ellipj
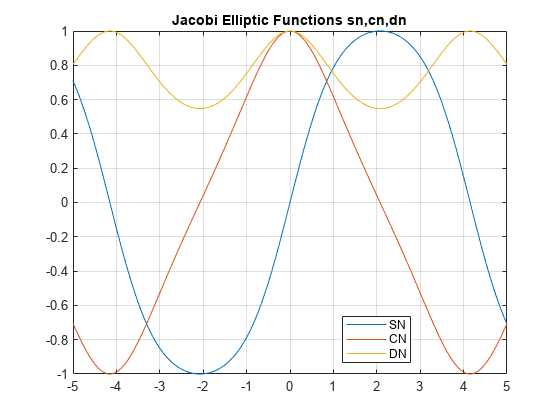
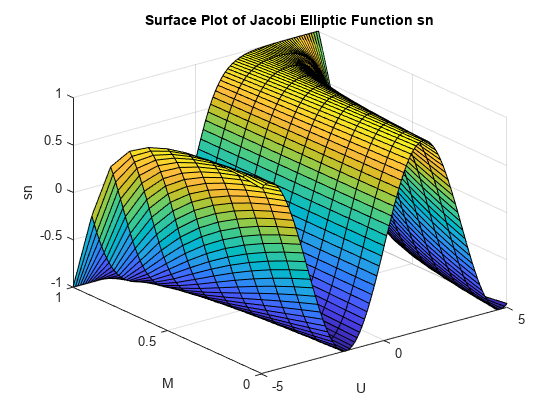
Jacobi elliptic functions
Description
Examples
Input Arguments
Output Arguments
More About
Algorithms
ellipj computes the Jacobi elliptic functions
using the method of the arithmetic-geometric mean of [1]. It
starts with the triplet of numbers
ellipj computes successive iterations using
Next, it calculates the amplitudes in radians using
being careful to unwrap the phases correctly. The Jacobian elliptic functions are then simply
References
[1] Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.
Extended Capabilities
Version History
Introduced before R2006a