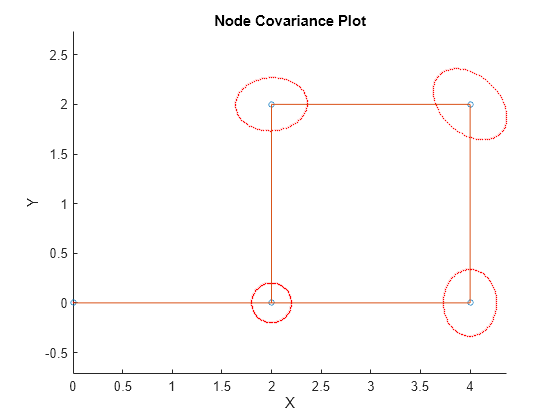
nodeCovariance

Get state covariance of nodes in factor graph

Since R2024b

Syntax

covariance = nodeCovariance(fg,nodeIDs)

Description

covariance = nodeCovariance(fg,nodeIDs) gets the stored covariances of nodes with the specified node IDs in the specified factor graph. You must optimize the factor graph using the optimize function with covariance estimation enabled before you can retrieve the stored node covariances. For more information about the covariance estimation algorithm and enabling covariance estimation, see the optimize and factorGraphSolverOptions object, respectively.

Examples

Get Node State Covariance from Factor Graph

Create a factor graph with 5 pose nodes. To make it easier to see the change in node state covariance in this example, specify the same information matrix for all factors.

fg = factorGraph;
f1 = factorTwoPoseSE2([1 2],Measurement=[2 0 0],Information=[25 0 0; 0 25 0; 0 0 100]);
f2 = factorTwoPoseSE2([2 3],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
f3 = factorTwoPoseSE2([3 4],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
f4 = factorTwoPoseSE2([4 5],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
addFactor(fg,f1);
addFactor(fg,f2);
addFactor(fg,f3);
addFactor(fg,f4);

Add a loop closure between the second and fifth nodes using a factor.

f5 = factorTwoPoseSE2([5 2],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
addFactor(fg,f5);

Fix the first node and initialize the node states. The first state can stay at default.

fixNode(fg,1)
nodeState(fg,2:5,[2 0 0; 4 0 pi/2; 4 2 pi; 2 2 3*pi/2]);

Visualize the factor graph.

show(fg);
title("Factor Graph with Loop Closure Before Optimization")
axis equal
xlabel("X")
ylabel("Y")
hold on

Create factor graph solver options that indicate to the solver to estimate node state covariance for all types of nodes in the factor graph.

opts = factorGraphSolverOptions(StateCovarianceType="all-types");

Optimize the graph with the custom options to estimate and store the node state covariance.

optimize(fg,opts);

Get the node IDs of the SE(2) pose nodes and get their state covariance matrices.

se2nodes = nodeIDs(fg,NodeType="POSE_SE2");
se2Cov = nodeCovariance(fg,se2nodes);

Extract the diagonal elements of the state covariance matrices. Note that the state covariance values of the first node are zeros because that node is fixed.

se2Cov2Diag = [diag(se2Cov(:,:,1))';
               diag(se2Cov(:,:,2))';
               diag(se2Cov(:,:,3))';
               diag(se2Cov(:,:,4))';
               diag(se2Cov(:,:,5))']

se2Cov2Diag = 5×3

         0         0         0
    0.0400    0.0400    0.0100
    0.0720    0.1120    0.0165
    0.1380    0.1280    0.0180
    0.1300    0.0720    0.0165

Plot the node state covariances. Note that the plotted covariance increases due to drift accumulation with each consecutive node until node 5, which has a lower covariance due to the additional state information provided by the loop closure.

states = nodeState(fg,se2nodes);
exampleHelperPlot2DCovariance(se2Cov,states);
title("Node Covariance Plot")
axis equal

Input Arguments

fg — Factor graph

factorGraph object

Factor graph, specified as a factorGraph object.

nodeIDs — IDs of nodes for which to retrieve state covariances

N-element row vector of nonnegative integers

IDs of nodes for which to retrieve state covariances, specified as an N-element row vector of nonnegative integers. N is the number of specified node IDs.

All node IDs must specify nodes of the same type. And to get the node state covariance for any nodes, you must first optimize the factor graph with custom solver options that specify which node type for which to estimate and store state covariance. To specify the node type to use, set the StateCovarianceType property of the factorGraphSolverOptions object to one or more desired node types.

Output Arguments

covariance — Node state covariances

M-by-M-by-N array

Node state covariances, returned as an M-by-M-by-N array. Each page in the array represents the state covariance matrix for a node. N is the number of specified node IDs.

The size of the covariance matrices depends on the node type of the specified node IDs:

• "POSE_SE2" — 3-by-3 matrix

• "POSE_SE3" — 7-by-7 matrix

• "POINT_XY" — 2-by-2 matrix

• "POINT_XYZ" — 3-by-3 matrix

• "IMU_BIAS" — 6-by-6 matrix

• "VEL3" — 3-by-3 matrix

Note

To get the node state covariance for a node type, you must first optimize the factor graph with custom solver options that specify the node type for which to estimate and store state covariance. To specify the node type to use, set the StateCovarianceType property of the factorGraphSolverOptions object to one or more desired node types.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

When generating portable C code with a C++ compiler, you must specify hierarchical packing with non-minimal headers. For more information on packaging options, see the packNGo (MATLAB Coder) function.

Version History

Introduced in R2024b