Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

dist

Distance angulaire en radians

Syntaxe

distance = dist(quatA,quatB)

Description

distance = dist(quatA,quatB) renvoie la distance angulaire en radians entre deux quaternions, quatA et quatB.

Exemples

Calculer la distance du quaternion

Calculez la distance quaternion entre un seul quaternion et chaque élément d'un vecteur de quaternions. Définissez les quaternions en utilisant les angles d'Euler.

q = quaternion([0,0,0],"eulerd","ZYX","frame")

q = quaternion
     1 + 0i + 0j + 0k

qArray = quaternion([0,45,0;0,90,0;0,180,0;0,-90,0;0,-45,0],"eulerd","ZYX","frame")

qArray = 5x1 quaternion array
       0.92388 +         0i +   0.38268j +         0k
       0.70711 +         0i +   0.70711j +         0k
    6.1232e-17 +         0i +         1j +         0k
       0.70711 +         0i -   0.70711j +         0k
       0.92388 +         0i -   0.38268j +         0k

quaternionDistance = rad2deg(dist(q,qArray))

quaternionDistance = 5×1

   45.0000
   90.0000
  180.0000
   90.0000
   45.0000

Si les deux arguments de dist sont des vecteurs, la distance du quaternion est calculée entre les éléments correspondants. Calculez la distance quaternion entre deux vecteurs quaternions.

angles1 = [30,0,15; ...
           30,5,15; ...
           30,10,15; ...
           30,15,15];
angles2 = [30,6,15; ...
           31,11,15; ...
           30,16,14; ...
           30.5,21,15.5];

qVector1 = quaternion(angles1,"eulerd","ZYX","frame");
qVector2 = quaternion(angles2,"eulerd","ZYX","frame");

rad2deg(dist(qVector1,qVector2))

ans = 4×1

    6.0000
    6.0827
    6.0827
    6.0287

Notez qu'un quaternion représente la même rotation que son négatif. Calculez un quaternion et son négatif.

qPositive = quaternion([30,45,-60],"eulerd","ZYX","frame")

qPositive = quaternion
     0.72332 - 0.53198i + 0.20056j +  0.3919k

qNegative = -qPositive

qNegative = quaternion
    -0.72332 + 0.53198i - 0.20056j -  0.3919k

Trouvez la distance entre le quaternion et son négatif.

dist(qPositive,qNegative)

ans = 0

Les composantes d’un quaternion peuvent être différentes des composantes de son négatif, mais les deux expressions représentent la même rotation.

Arguments d'entrée

quatA,quatB — Quaternions pour calculer la distance entre

quaternion objets | tableaux d'objets quaternion

Quaternions pour calculer la distance entre, spécifiés comme objets quaternion séparés par des virgules ou tableaux d'objets quaternion de toute dimensionnalité. quatA et quatB doivent avoir des tailles compatibles :

• size(quatA) == size(quatB), ou

• numel(quatA) == 1, ou

• numel(quatB) == 1, ou

• si [Adim1,…,AdimN] = size(quatA) et [Bdim1,…,BdimN] = size(quatB), alors pour i = 1:N, soit Adimi==Bdimi ou Adim==1 ou Bdim==1.

  Si l'un des arguments du quaternion ne contient qu'un seul quaternion, alors cette fonction renvoie les distances entre ce quaternion et chaque quaternion de l'autre argument.

Arguments de sortie

distance — Distance angulaire (radians)

scalaire numérique | tableau numérique

Distance angulaire en radians, renvoyée sous forme de scalaire numérique ou de tableau numérique. Les dimensions sont le maximum de l'union de size(quatA) et size(quatB).

Types de données : single | double

Algorithmes

La fonction dist renvoie la distance angulaire entre deux quaternions.

Un quaternion peut être défini par un axe (u_b,u_c,u_d) et un angle de rotation θ_q: $$q=\cos \left(\raisebox{1ex}{${\theta }_q$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)+\sin \left(\raisebox{1ex}{${\theta }_q$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\left(u_b\text{i}+u_c\text{j}+u_d\text{k}\right)$$.

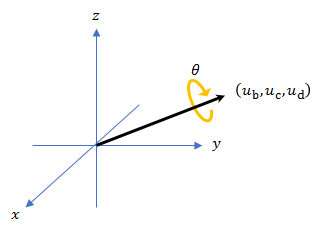
Étant donné un quaternion sous la forme $$q=a+b\text{i}+c\text{j}+d\text{k}$$, où a est la partie réelle, vous pouvez résoudre l'angle de q comme $${\theta }_q=2{\cos }^{-1}(a)$$.

Considérons deux quaternions, p et q, et le produit $$z=p*\text{conjugate}(q)$$. Lorsque p se rapproche de q, l'angle de z passe à 0, et z se rapproche de l'unité. quaternion.

La distance angulaire entre deux quaternions peut être exprimée par $${\theta }_{\text{z}}=2{\cos }^{-1}\left(\text{real}\left(z\right)\right)$$.

En utilisant la syntaxe du type de données quaternion , la distance angulaire est calculée comme suit :

angularDistance = 2*acos(abs(parts(p*conj(q))));

Capacités étendues

Génération de code C/C++
Générez du code C et C++ avec MATLAB® Coder™.

Historique des versions

Introduit dans R2019b

Voir aussi

Fonctions

• parts | conj

Objets

• quaternion

Rubriques

• Rotations, Orientation, and Quaternions