Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

point de rotation

Rotation des points de quaternion

Syntaxe

rotationResult = rotatepoint(quat,cartesianPoints)

Description

rotationResult = rotatepoint(quat,cartesianPoints) fait pivoter les points cartésiens à l'aide du quaternion, quat. Les éléments du quaternion sont normalisés avant utilisation dans la rotation.

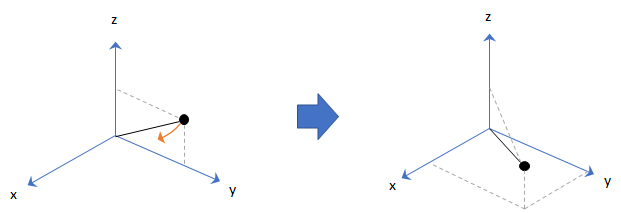
Exemples

Faire pivoter le point à l'aide du vecteur quaternion

Définir un point en trois dimensions. Les coordonnées d'un point sont toujours spécifiées dans l'ordre x, y, z. Pour une visualisation pratique, définissez le point sur le plan x-y.

x = 0.5;
y = 0.5;
z = 0;

plot(x,y,"ko")
hold on
axis([-1 1 -1 1])

Créez un vecteur quaternion spécifiant deux rotations distinctes, une pour faire pivoter le point de 45 et une autre pour faire pivoter le point de -90 degrés autour de l'axe z. Utilisez rotatepoint pour effectuer la rotation.

quat = quaternion([0,0,pi/4; ...
                   0,0,-pi/2],"euler","XYZ","point");
               
rotatedPoint = rotatepoint(quat,[x,y,z])

rotatedPoint = 2×3

   -0.0000    0.7071         0
    0.5000   -0.5000         0

Tracez les points pivotés.

plot(rotatedPoint(1,1),rotatedPoint(1,2),"bo")
plot(rotatedPoint(2,1),rotatedPoint(2,2),"go")

Faire pivoter un groupe de points à l'aide du quaternion

Définissez deux points dans un espace tridimensionnel. Définissez un quaternion pour faire pivoter le point en tournant d'abord autour de l'axe z de 30 degrés, puis autour du nouvel axe y de 45 degrés.

a = [1,0,0];
b = [0,1,0];
quat = quaternion([30,45,0],"eulerd","ZYX","point");

Utilisez rotatepoint pour faire pivoter les deux points à l'aide de l'opérateur de rotation quaternion. Affichez le résultat.

rP = rotatepoint(quat,[a;b])

rP = 2×3

    0.6124    0.5000   -0.6124
   -0.3536    0.8660    0.3536

Visualisez l'orientation d'origine et l'orientation pivotée des points. Tracez des lignes depuis l'origine jusqu'à chacun des points à des fins de visualisation.

plot3(a(1),a(2),a(3),"bo");

hold on
grid on
axis([-1 1 -1 1 -1 1])
xlabel("x")
ylabel("y")
zlabel("z")

plot3(b(1),b(2),b(3),"ro")
plot3(rP(1,1),rP(1,2),rP(1,3),"bd")
plot3(rP(2,1),rP(2,2),rP(2,3),"rd")

plot3([0;rP(1,1)],[0;rP(1,2)],[0;rP(1,3)],"k")
plot3([0;rP(2,1)],[0;rP(2,2)],[0;rP(2,3)],"k")
plot3([0;a(1)],[0;a(2)],[0;a(3)],"k")
plot3([0;b(1)],[0;b(2)],[0;b(3)],"k")

Arguments d'entrée

quat — Quaternion qui définit la rotation

Objet quaternion | vecteur d'objets quaternion

Quaternion qui définit la rotation, spécifié comme un objet quaternion ou un vecteur d'objets quaternion . quat et cartesianPoints doivent avoir des tailles compatibles :

• length(quat) == size(cartesianPoints,1), ou

• length(quat) == 1, ou

• size(cartesianPoints,1) == 1

cartesianPoints — Points cartésiens tridimensionnels

Vecteur numérique 1 x 3 | N-matrice numérique par 3

Points cartésiens tridimensionnels, spécifiés sous la forme d'un vecteur numérique 1 sur 3 représentant un seul point ou d'une matrice numérique N-par 3 représentant des points N . quat et cartesianPoints doivent avoir des tailles compatibles :

• length(quat) == size(cartesianPoints,1) ou

• length(quat) == 1, ou

• size(cartesianPoints,1) == 1

Types de données : single | double

Arguments de sortie

rotationResult — Points cartésiens repositionnés

Vecteur numérique 1 x 3 | matrice numérique

Points cartésiens pivotés définis à l'aide de la rotation des quaternions, renvoyés sous forme de vecteur numérique 1 x 3 ou de matrice numérique.

rotationResult est un vecteur 1 par 3 lorsque quat est un objet scalaire quaternion et cartesianPoints est un vecteur 1 sur 3 représentant un seul point. Sinon, rotationResult est une matrice M-par 3, où M est le maximum de length(quat) et size(cartesianPoints,1).

Types de données : single | double

Algorithmes

La rotation du point du quaternion fait tourner un point spécifié dans R³ selon un quaternion spécifié :

$$L_q(u)=qu{q}^{*}$$

où q est le quaternion, * représente la conjugaison, et u est le point à faire pivoter, spécifié comme quaternion.

Pour plus de commodité, la fonction rotatepoint prend un point dans R³ et renvoie un point dans R³. Étant donné un appel de fonction avec un quaternion arbitraire, q = a + bi + cj + dk, et une coordonnée arbitraire, [x,y,z], par exemple,

rereferencedPoint = rotatepoint(q,[x,y,z])

la fonction rotatepoint effectue les opérations suivantes :

1. Convertit le point [x,y,z] en quaternion :

   $$u_q=0+xi+yj+zk$$

2. Normalise le quaternion, q:

   $$q_n=\frac{q}{\sqrt{a^2+b^2+c^2+d^2}}$$

3. Applique la rotation :

   $$v_q=q{u}_q{q}^{*}$$

4. Convertit la sortie du quaternion, v_q, en R³

Capacités étendues

Génération de code C/C++
Générez du code C et C++ avec MATLAB® Coder™.

Historique des versions

Introduit dans R2019b

Voir aussi

Fonctions

• rotateframe

Objets

• quaternion

Rubriques

• Rotations, Orientation, and Quaternions