Utiliser FFT2 sur le GPU pour simuler des modèles de diffraction

Définir le système de coordonnées

Avant de simuler la lumière qui a traversé une ouverture, définissez un système de coordonnées. Pour obtenir le comportement numérique correct pour l'appel de fft2, organisez x et y de sorte que la valeur zéro soit au bon endroit.

N2 représente la moitié de la taille dans chaque dimension.

N2 = gpuArray(1024);
[gx,gy] = meshgrid(-1:1/N2:(N2-1)/N2);

Simuler le motif de diffraction pour une ouverture rectangulaire

Simulez l’effet du passage d’un faisceau parallèle de lumière monochromatique à travers une petite ouverture rectangulaire. La transformée de Fourier bidimensionnelle décrit le champ lumineux à une grande distance de l'ouverture. Commencez par former aperture comme un masque logique basé sur le système de coordonnées. La source lumineuse est une version double précision de l'ouverture. Le signal lumineux en champ lointain est trouvé à l'aide de fft2 .

aperture = (abs(gx)<4/N2).*(abs(gy)<2/N2);
lightsource = double(aperture);
farfieldsignal = fft2(lightsource);

Afficher l'intensité lumineuse pour une ouverture rectangulaire

Calculez l'intensité lumineuse en champ lointain à partir de la magnitude au carré du champ lumineux. Utilisez fftshift pour faciliter la visualisation.

farfieldintensity = real(farfieldsignal.*conj(farfieldsignal));

imagesc(fftshift(farfieldintensity));
axis("equal");
axis("off");
title("Rectangular Aperture Far-field Diffraction Pattern");

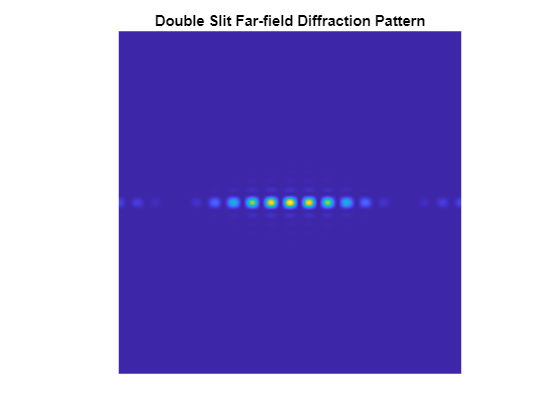
Simuler l'expérience de la double fente de Young

L'une des expériences les plus célèbres en optique est l'expérience de la double fente de Young, qui montre l'interférence lumineuse lorsqu'une ouverture comprend deux fentes parallèles. Une série de points brillants est visible là où une interférence constructive a lieu. Former l'ouverture représentant deux fentes. Limitez l'ouverture dans la direction y pour garantir que le motif résultant ne soit pas entièrement concentré le long de l'axe horizontal.

slits = (abs(gx)<=10/N2).*(abs(gx)>=8/N2);
aperture = slits.*(abs(gy)<20/N2);
lightsource = double(aperture);
farfieldsignal = fft2(lightsource);

Afficher l'intensité lumineuse pour la double fente de Young

Calculez et affichez l’intensité comme précédemment.

farfieldintensity = real(farfieldsignal.*conj(farfieldsignal));
imagesc(fftshift(farfieldintensity));
axis("equal"); 
axis("off");
title("Double Slit Far-field Diffraction Pattern");