Create Weighted Lifetime PD Model
This example shows how to use fitLifetimePDModel to create a PD model using weighted credit and macroeconomic data.
Load Data
Load the credit portfolio data.
load RetailCreditPanelData.matJoin the two data components into a single data set.
data = join(data,dataMacro); disp(head(data))
ID ScoreGroup YOB Default Year GDP Market
__ __________ ___ _______ ____ _____ ______
1 Low Risk 1 0 1997 2.72 7.61
1 Low Risk 2 0 1998 3.57 26.24
1 Low Risk 3 0 1999 2.86 18.1
1 Low Risk 4 0 2000 2.43 3.19
1 Low Risk 5 0 2001 1.26 -10.51
1 Low Risk 6 0 2002 -0.59 -22.95
1 Low Risk 7 0 2003 0.63 2.78
1 Low Risk 8 0 2004 1.85 9.48
Create Weights Variable
To create a weighted lifetime PD model, you need a weights variable. In this example, you create a weights variable by exponentially weighting recent data more heavily than older data. Give the most recent year (2004) a weight of 1, then shrink the weight for each preceding year by a factor of 0.96 relative to the year after. Display the data and weights.
% Get a list of years in the data set Years = unique(data.Year); n = size(Years,1); % Initialize weights YearWeights = zeros(n,1); w = 1; % The most recent year (2004) has a weight of 1, the weight for each preceding % year is shrunk by a factor of .96 relative to the year after. for i = n:-1:1 YearWeights(i) = w; w = w*.96; end % Put the weights for each year in a table, so you can use join YearWeights = table(Years, YearWeights,'VariableNames',{'Year','YearWeights'}); data = join(data,YearWeights,'Keys','Year'); % Show the weighted data disp(head(data))
ID ScoreGroup YOB Default Year GDP Market YearWeights
__ __________ ___ _______ ____ _____ ______ ___________
1 Low Risk 1 0 1997 2.72 7.61 0.75145
1 Low Risk 2 0 1998 3.57 26.24 0.78276
1 Low Risk 3 0 1999 2.86 18.1 0.81537
1 Low Risk 4 0 2000 2.43 3.19 0.84935
1 Low Risk 5 0 2001 1.26 -10.51 0.88474
1 Low Risk 6 0 2002 -0.59 -22.95 0.9216
1 Low Risk 7 0 2003 0.63 2.78 0.96
1 Low Risk 8 0 2004 1.85 9.48 1
Partition Data
Partition the data into training and test sets.
nIDs = max(data.ID); uniqueIDs = unique(data.ID); rng('default'); % For reproducibility c = cvpartition(nIDs,'HoldOut',0.4); TrainIDInd = training(c); TestIDInd = test(c); TrainDataInd = ismember(data.ID,uniqueIDs(TrainIDInd)); TestDataInd = ismember(data.ID,uniqueIDs(TestIDInd));
Create a Lifetime PD Model
Select a ModelType for the lifetime PD model, then use fitLifetimePDModel to fit a weighted model using the WeightsVar name-value argument.
ModelType =  "Probit"
"Probit"ModelType = "Probit"
pdModel = fitLifetimePDModel(data(TrainDataInd,:),ModelType,... AgeVar="YOB", ... IDVar="ID", ... LoanVars="ScoreGroup", ... MacroVars={'GDP','Market'}, ... ResponseVar="Default",WeightsVar='YearWeights'); disp(pdModel)
Probit with properties:
ModelID: "Probit"
Description: ""
UnderlyingModel: [1×1 classreg.regr.CompactGeneralizedLinearModel]
IDVar: "ID"
AgeVar: "YOB"
LoanVars: "ScoreGroup"
MacroVars: ["GDP" "Market"]
ResponseVar: "Default"
WeightsVar: "YearWeights"
TimeInterval: 1
Display the underlying model.
disp(pdModel.UnderlyingModel)
Compact generalized linear regression model:
probit(Default) ~ 1 + ScoreGroup + YOB + GDP + Market
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ ___________
(Intercept) -1.6275 0.040249 -40.434 0
ScoreGroup_Medium Risk -0.26616 0.015304 -17.392 9.4854e-68
ScoreGroup_Low Risk -0.46622 0.017631 -26.443 4.3347e-154
YOB -0.11399 0.005209 -21.884 3.7215e-106
GDP -0.04152 0.015646 -2.6537 0.0079608
Market -0.0029277 0.0011321 -2.5861 0.0097068
388097 observations, 388091 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 1.63e+03, p-value = 0
Validate Model
Use modelDiscrimination to view the area under ROC curve (AUROC) metric for different segments of the validation data. When ShowDetails = true, you have three extra columns in the DiscMeasure output: Segment, SegmentCount, and WeightedCount. Segment shows the segmentation variable value corresponding to the given row. SegmentCount gives the number of data points contained by the given segment, while WeightedCount shows the sum of the weights associated with the segment's data. The default weight for each row is 1, so if WeightsVar is not specified or doesn't exist in the validation data set, then WeightedCount is equal to SegmentCount.
DataSetChoice ="Testing"; if DataSetChoice=="Training" Ind = TrainDataInd; else Ind = TestDataInd; end DiscMeasure = modelDiscrimination(pdModel,data(Ind,:),SegmentBy="ScoreGroup",ShowDetails=true)
DiscMeasure=3×4 table
AUROC Segment SegmentCount WeightedCount
_______ _____________ ____________ _____________
Probit, ScoreGroup=High Risk 0.64562 "High Risk" 84242 74228
Probit, ScoreGroup=Medium Risk 0.62503 "Medium Risk" 87397 77172
Probit, ScoreGroup=Low Risk 0.63367 "Low Risk" 86988 76910
disp(DiscMeasure)
AUROC Segment SegmentCount WeightedCount
_______ _____________ ____________ _____________
Probit, ScoreGroup=High Risk 0.64562 "High Risk" 84242 74228
Probit, ScoreGroup=Medium Risk 0.62503 "Medium Risk" 87397 77172
Probit, ScoreGroup=Low Risk 0.63367 "Low Risk" 86988 76910
Use modelDiscriminationPlot to visualize the ROC curve. The plotted curve accounts for the specified weights.
modelDiscriminationPlot(pdModel,data(Ind,:),SegmentBy="ScoreGroup")
Use modelCalibration to evaluate the model performance. The modelCalibration function requires a grouping variable and compares the observed weighted default rate in the group with the weighted average predicted PD for the group.
[CalMeasure, CalData] = modelCalibration(pdModel,data(Ind,:),{'YOB','ScoreGroup'});
disp(CalMeasure) RMSE
_________
Probit, grouped by YOB, ScoreGroup 0.0011458
The CalData output also contains a WeightedCount column that is similar to DiscMeasure and shows the sum of the weights associated with the given group. The default weight is 1 for each row, so if WeightsVar is unspecified, or if the variable does not exist in the validation set, WeightedCount is equal to GroupCount.
disp(CalData)
ModelID YOB ScoreGroup PD GroupCount WeightedCount
__________ ___ ___________ __________ __________ _____________
"Observed" 1 High Risk 0.030861 13084 10220
"Observed" 1 Medium Risk 0.013521 12998 10154
"Observed" 1 Low Risk 0.0081327 12646 9879.8
"Observed" 2 High Risk 0.022938 12567 10224
"Observed" 2 Medium Risk 0.012437 12767 10391
"Observed" 2 Low Risk 0.0046497 12478 10156
"Observed" 3 High Risk 0.017818 12067 10223
"Observed" 3 Medium Risk 0.0093478 12520 10613
"Observed" 3 Low Risk 0.0058731 12386 10500
"Observed" 4 High Risk 0.018711 11798 10410
"Observed" 4 Medium Risk 0.0094983 12325 10881
"Observed" 4 Low Risk 0.0044163 12295 10857
"Observed" 5 High Risk 0.016317 11481 10551
"Observed" 5 Medium Risk 0.0080286 12120 11145
"Observed" 5 Low Risk 0.0041782 12217 11236
"Observed" 6 High Risk 0.0096414 11250 10770
"Observed" 6 Medium Risk 0.0054967 11996 11491
"Observed" 6 Low Risk 0.0031086 12138 11629
"Observed" 7 High Risk 0.0058197 7937 7773.6
"Observed" 7 Medium Risk 0.0032354 8334 8159.8
"Observed" 7 Low Risk 0.0015307 8459 8283.6
"Observed" 8 High Risk 0.0022178 4058 4058
"Observed" 8 Medium Risk 0.0009223 4337 4337
"Observed" 8 Low Risk 0.00068666 4369 4369
"Probit" 1 High Risk 0.027597 13084 10220
"Probit" 1 Medium Risk 0.014522 12998 10154
"Probit" 1 Low Risk 0.008584 12646 9879.8
"Probit" 2 High Risk 0.021447 12567 10224
"Probit" 2 Medium Risk 0.011013 12767 10391
"Probit" 2 Low Risk 0.0063911 12478 10156
"Probit" 3 High Risk 0.019195 12067 10223
"Probit" 3 Medium Risk 0.0097721 12520 10613
"Probit" 3 Low Risk 0.00563 12386 10500
"Probit" 4 High Risk 0.018073 11798 10410
"Probit" 4 Medium Risk 0.0091654 12325 10881
"Probit" 4 Low Risk 0.0052668 12295 10857
"Probit" 5 High Risk 0.014643 11481 10551
"Probit" 5 Medium Risk 0.0072 12120 11145
"Probit" 5 Low Risk 0.0040669 12217 11236
"Probit" 6 High Risk 0.010323 11250 10770
"Probit" 6 Medium Risk 0.0049299 11996 11491
"Probit" 6 Low Risk 0.0027131 12138 11629
"Probit" 7 High Risk 0.0063338 7937 7773.6
"Probit" 7 Medium Risk 0.002904 8334 8159.8
"Probit" 7 Low Risk 0.0015449 8459 8283.6
"Probit" 8 High Risk 0.0040971 4058 4058
"Probit" 8 Medium Risk 0.0018064 4337 4337
"Probit" 8 Low Risk 0.00093487 4369 4369
Use modelCalibrationPlot to visualize the observed weighted default rates compared to the predicted PD.
modelCalibrationPlot(pdModel,data(Ind,:),{'YOB','ScoreGroup'})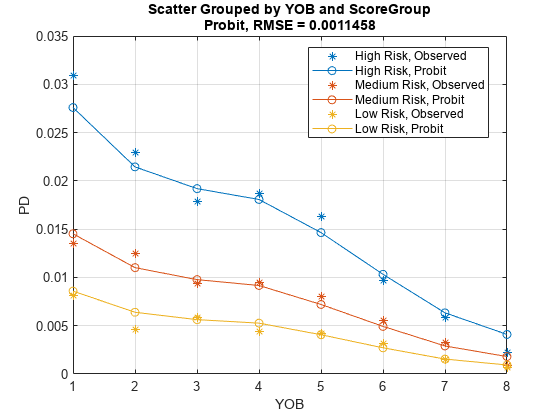
See Also
fitLifetimePDModel | Logistic | Probit | Cox | customLifetimePDModel | predict | predictLifetime | modelDiscrimination | modelCalibration | modelDiscriminationPlot | modelCalibrationPlot | portfolioECL
Topics
- Basic Lifetime PD Model Validation
- Compare Logistic Model for Lifetime PD to Champion Model
- Compare Lifetime PD Models Using Cross-Validation
- Expected Credit Loss Computation
- Incorporate Macroeconomic Scenario Projections in Loan Portfolio ECL Calculations
- Compare Model Discrimination and Model Calibration to Validate of Probability of Default
- Compare Probability of Default Using Through-the-Cycle and Point-in-Time Models
- Create Custom Lifetime PD Model for Decision Tree Model with Function Handle
- Create Custom Lifetime PD Model for Credit Scorecard Model with Function Handle
- Incorporate Macroeconomic Scenario Projections in Loan Portfolio ECL Calculations