besseli

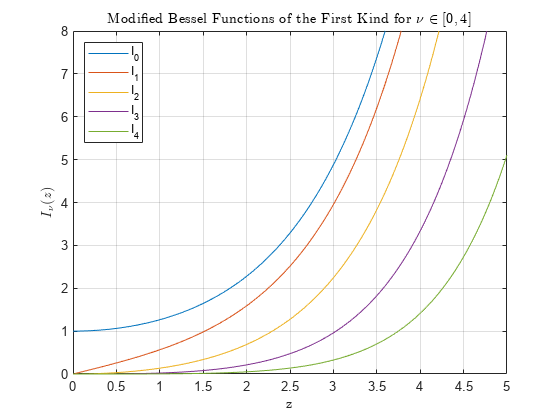
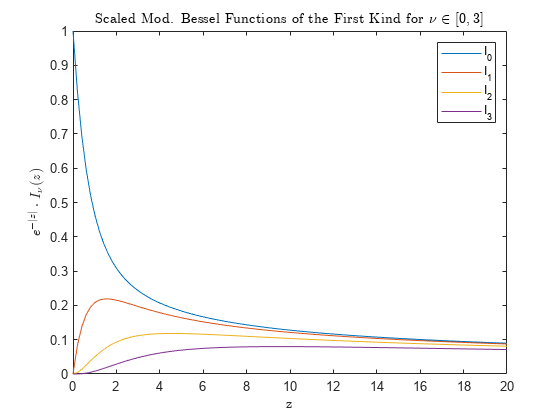
Modified Bessel function of first kind

Syntax

I = besseli(nu,Z)

I = besseli(nu,Z,scale)

Description

I = besseli(nu,Z) computes the modified Bessel function of the first kind I_ν(z) for each element in array Z.

I = besseli(nu,Z,scale) specifies whether to exponentially scale the modified Bessel function of the first kind to avoid overflow or loss of accuracy. If scale is 1, then the output of besseli is scaled by the factor exp(-abs(real(Z))).

Examples

Plot Modified Bessel Functions of First Kind

Define the domain.

z = 0:0.01:5;

Calculate the first five modified Bessel functions of the first kind. Each row of I contains the values of one order of the function evaluated at the points in z.

I = zeros(5,501);
for nu = 0:4
    I(nu+1,:) = besseli(nu,z);
end

Plot all of the functions in the same figure.

plot(z,I)
axis([0 5 0 8])
grid on
legend('I_0','I_1','I_2','I_3','I_4','Location','NorthWest')
title('Modified Bessel Functions of the First Kind for $\nu \in [0,4]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$I_\nu(z)$','interpreter','latex')

Calculate Exponentially Scaled Modified Bessel Functions

Calculate the scaled modified Bessel function of the first kind ${\mathit{I}}_{\nu }\left(\mathit{z}\right)\cdot {\mathit{e}}^{-\left|\mathrm{Re}\left[\mathit{Z}\right]\right|}$ for values of $\mathit{z}$ in the interval $\left[0,20\right]$ and for orders $\nu$ between 0 and 3.

z = linspace(0,20);
scale = 1;
Is = zeros(4,100);
for nu = 0:3
  Is(nu+1,:) = besseli(nu,z,scale);
end

Plot all of the functions in the same figure. For large values of $\mathit{z}$, the scaled functions do not overflow the limits of double precision, extending their range of computability compared to the unscaled functions.

plot(z,Is)
legend('I_0','I_1','I_2','I_3')
title('Scaled Mod. Bessel Functions of the First Kind for $\nu \in \left[0, 3 \right]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$e^{-|{z}|} \cdot I_\nu(z)$','interpreter','latex')

Input Arguments

nu — Equation order

scalar | vector | matrix | multidimensional array

Equation order, specified as a scalar, vector, matrix, or multidimensional array. nu is a real number that specifies the order of the modified Bessel function of the first kind. nu and Z must be the same size, or one of them can be scalar.

Example: besseli(3,Z)

Data Types: single | double

Z — Functional domain

scalar | vector | matrix | multidimensional array

Functional domain, specified as a scalar, vector, matrix, or multidimensional array. besseli is real-valued where Z is positive. nu and Z must be the same size, or one of them can be scalar.

Example: besseli(nu,[1-1i 1+0i 1+1i])

Data Types: single | double
Complex Number Support: Yes

scale — Toggle to scale function

0 (default) | 1

Toggle to scale function, specified as one of these values:

• 0 (default) — No scaling

• 1 — Scale the output of besseli by exp(-abs(real(Z)))

The magnitude of besseli grows rapidly as the value of abs(real(Z)) increases, so exponentially scaling the output is useful for large values of abs(real(Z)), where the results otherwise quickly lose accuracy or overflow the limits of double precision.

Example: besseli(nu,Z,1)

More About

Modified Bessel Functions

This differential equation, where ν is a real constant, is called the modified Bessel's equation:

$$z^2\frac{d^{2}y}{d{z}^2}+z\frac{dy}{dz}-\left(z^2+{\nu }^2\right)y=0.$$

Its solutions are known as modified Bessel functions.

The modified Bessel functions of the first kind, denoted I_ν(z) and I_–ν(z), form a fundamental set of solutions of the modified Bessel's equation. I_ν(z) is defined by

$$I_{\nu }(z)={\left(\frac{z}{2}\right)}^{\nu }{\displaystyle \sum }_{(k=0)}^{\infty }\frac{{\left(\frac{z^2}{4}\right)}^k}{k!\Gamma (\nu +k+1)}.$$

The modified Bessel functions of the second kind, denoted K_ν(z), form a second solution independent of I_ν(z) given by

$$K_{\nu }(z)=\left(\frac{\pi }{2}\right)\frac{I_{-\nu }(z)-I_{\nu }(z)}{\sin (\nu \pi )}.$$

You can compute the modified Bessel functions of the second kind using besselk.

References

[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

The besseli function fully supports tall arrays. For more information, see Tall Arrays.

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Always returns a complex result.

• Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

• Always returns a complex result.

• Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The besseli function supports GPU array input with these usage notes and limitations:

• The order nu must contain nonnegative real values.

• The argument Z must contain nonnegative real values.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a