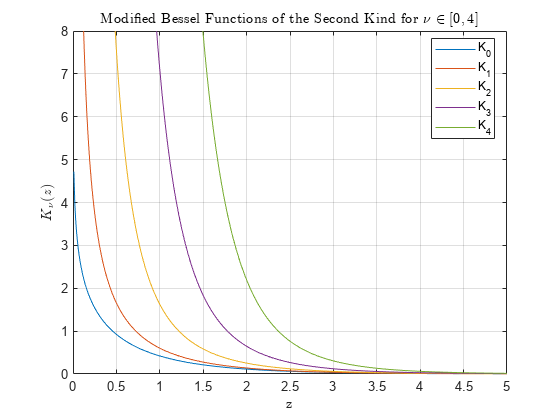
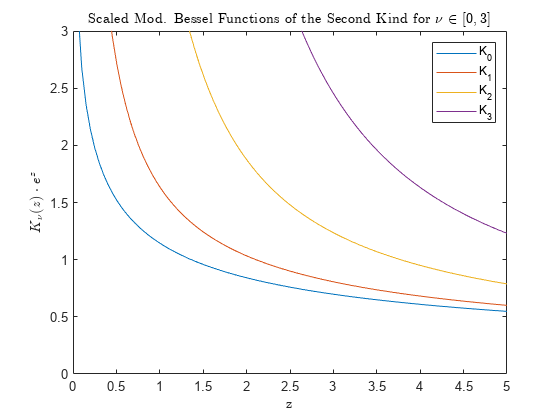
besselk

Modified Bessel function of second kind

Syntax

K = besselk(nu,Z)

K = besselk(nu,Z,scale)

Description

K = besselk(nu,Z) computes the modified Bessel function of the second kind K_ν(z) for each element in array Z.

K = besselk(nu,Z,scale) specifies whether to exponentially scale the modified Bessel function of the second kind to avoid underflow or loss of accuracy. If scale is 1, then the output of besselk is scaled by a factor exp(Z).

Examples

Plot Modified Bessel Functions of Second Kind

Define the domain.

z = 0:0.01:5;

Calculate the first five modified Bessel functions of the second kind. Each row of K contains the values of one order of the function evaluated at the points in z.

K = zeros(5,501);
for i = 0:4
    K(i+1,:) = besselk(i,z);
end

Plot all of the functions in the same figure.

plot(z,K)
axis([0 5 0 8])
grid on
legend('K_0','K_1','K_2','K_3','K_4','Location','Best')
title('Modified Bessel Functions of the Second Kind for $\nu \in [0,4]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$K_\nu(z)$','interpreter','latex')

Calculate Exponentially Scaled Modified Bessel Functions

Calculate the scaled modified Bessel functions of the second kind ${\mathit{K}}_{\nu }\left(\mathit{z}\right)\cdot {\mathit{e}}^{\mathit{z}}$ for values of $\mathit{z}$ in the interval $\left[0,5\right]$ and for orders of $\nu$ between 0 and 3.

z = linspace(0,5);
scale = 1;
Ks = zeros(4,100);
for nu = 0:3
  Ks(nu+1,:) = besselk(nu,z,scale);
end

Plot all of the functions in the same figure. For large values of $\mathit{z}$, the scaled functions do not underflow the limits of double precision as quickly as the unscaled functions, extending their range of computability.

plot(z,Ks)
ylim([0 3])
legend('K_0','K_1','K_2','K_3')
title('Scaled Mod. Bessel Functions of the Second Kind for $\nu \in \left[0, 3 \right]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$K_\nu(z) \cdot e^{z}$','interpreter','latex')

Input Arguments

nu — Equation order

scalar | vector | matrix | multidimensional array

Equation order, specified as a scalar, vector, matrix, or multidimensional array. nu is a real number that specifies the order of the modified Bessel function of the second kind. nu and Z must be the same size, or one of them can be scalar.

Example: besselk(3,Z)

Data Types: single | double

Z — Functional domain

scalar | vector | matrix | multidimensional array

Functional domain, specified as a scalar, vector, matrix, or multidimensional array. besselk is real-valued where Z is positive. nu and Z must be the same size, or one of them can be scalar.

Example: besselk(nu,0:3)

Data Types: single | double
Complex Number Support: Yes

scale — Toggle to scale function

0 (default) | 1

Toggle to scale function, specified as one of these values:

• 0 (default) — No scaling

• 1 — Scale the output of besselk by exp(Z)

The value of besselk decreases rapidly as the value of Z increases, so exponentially scaling the output is useful for large values of Z where the results otherwise quickly lose accuracy or underflow the limits of double precision.

Example: besselk(nu,Z,1)

More About

Modified Bessel Functions

This differential equation, where ν is a real constant, is called the modified Bessel's equation:

$$z^2\frac{d^{2}y}{d{z}^2}+z\frac{dy}{dz}-\left(z^2+{\nu }^2\right)y=0.$$

Its solutions are known as modified Bessel functions.

The modified Bessel functions of the first kind, denoted I_ν(z) and I_–ν(z), form a fundamental set of solutions of the modified Bessel's equation. I_ν(z) is defined by

$$I_{\nu }(z)={\left(\frac{z}{2}\right)}^{\nu }{\displaystyle \sum }_{(k=0)}^{\infty }\frac{{\left(\frac{z^2}{4}\right)}^k}{k!\Gamma (\nu +k+1)}.$$

You can compute the modified Bessel functions of the first kind using besseli.

The modified Bessel functions of the second kind, denoted K_ν(z), form a second solution independent of I_ν(z) given by

$$K_{\nu }(z)=\left(\frac{\pi }{2}\right)\frac{I_{-\nu }(z)-I_{\nu }(z)}{\sin (\nu \pi )}.$$

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. For more information, see Tall Arrays.

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Always returns a complex result.

• Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

• Always returns a complex result.

• Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

• The order nu must contain nonnegative real values.

• The argument Z must contain nonnegative real values.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a