cart2sph
Transform Cartesian coordinates to spherical
Description
Examples
Input Arguments
Output Arguments
Algorithms
The mapping from three-dimensional Cartesian coordinates to spherical coordinates is
azimuth = atan2(y,x) elevation = atan2(z,sqrt(x.^2 + y.^2)) r = sqrt(x.^2 + y.^2 + z.^2)
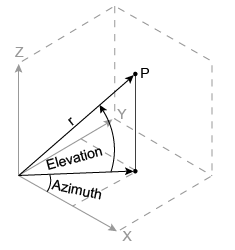
The notation for spherical coordinates is not standard. For
the cart2sph function, elevation is
measured from the x-y plane. Notice that if elevation
= 0, the point is in the x-y plane.
If elevation = pi/2, then the point is on the positive z-axis.
Extended Capabilities
Version History
Introduced before R2006a