Spherical Coordinates
Support for Spherical Coordinates
Spherical coordinates describe a vector or point in space with a distance and two angles. The distance, R, is the usual Euclidean norm. There are multiple conventions regarding the specification of the two angles. They include:
Azimuth and elevation angles
Phi and theta angles
u and v coordinates
Phased Array System Toolbox™ software natively supports the azimuth/elevation representation. The software also provides functions for converting between the azimuth/elevation representation and the other representations. See Phi and Theta Angles and U and V Coordinates.
Azimuth and Elevation Angles
In Phased Array System Toolbox software, the predominant convention for spherical coordinates is as follows:
Use the azimuth angle, az, and the elevation angle, el, to define the location of a point on the unit sphere.
Specify all angles in degrees.
List coordinates in the sequence (az,el,R).
The azimuth angle of a vector is the angle between the x-axis and the orthogonal projection of the vector onto the xy plane. The angle is positive in going from the x axis toward the y axis. Azimuth angles lie between –180 and 180 degrees. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy plane. By default, the boresight direction of an element or array is aligned with the positive x-axis. The boresight direction is the direction of the main lobe of an element or array.
Note
The elevation angle is sometimes defined in the literature as the angle a vector makes with the positive z-axis. The MATLAB® and Phased Array System Toolbox products do not use this definition.
This figure illustrates the azimuth angle and elevation angle for a vector shown as a green solid line.

Phi and Theta Angles
As an alternative to azimuth and elevation angles, you can use angles denoted by
φ and θ to express the location of a point
on the unit sphere. To convert the φ/θ representation to and from
the corresponding azimuth/elevation representation, use coordinate conversion
functions, phitheta2azel and azel2phitheta.
The phi angle (φ) is the angle from the positive y-axis to the vector’s orthogonal projection onto the yz plane. The angle is positive toward the positive z-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the x-axis to the vector itself. The angle is positive toward the yz plane. The theta angle is between 0 and 180 degrees.
The figure illustrates phi and theta for a vector that appears as a green solid line.

The coordinate transformations between φ/θ and az/el are described by the following equations
U and V Coordinates
In radar applications, it is often useful to parameterize the hemisphere x ≥ 0 using coordinates denoted by u and v.
To convert the φ/θ representation to and from the corresponding u/v representation, use coordinate conversion functions
phitheta2uvanduv2phitheta.To convert the azimuth/elevation representation to and from the corresponding u/v representation, use coordinate conversion functions
azel2uvanduv2azel.
You can define u and v in terms of φ and θ:
In these expressions, φ and θ are the phi and theta angles, respectively.
To convert azimuth and elevation to u and v use the transformation
which is valid only in the range abs(az)≤=90.
The values of u and v satisfy the inequalities
Conversely, the phi and theta angles can be written in terms of u and v using
The azimuth and elevation angles can also be written in terms of u and v:
Conversion between Rectangular and Spherical Coordinates
The following equations define the relationships between rectangular coordinates and the (az,el,R) representation used in Phased Array System Toolbox software.
To convert rectangular coordinates to (az,el,R):
To convert (az,el,R) to rectangular coordinates:
When specifying a target’s location with respect to a phased array, it is common to refer to its distance and direction from the array. The distance from the array corresponds to R in spherical coordinates. The direction corresponds to the azimuth and elevation angles.
Broadside Angles
Broadside angles are useful when describing the response of uniform linear arrays (ULA) to impinging signals. The array response depends directly on the broadside angle and not on the azimuth and elevation angles individually. The figure below shows a ULA with elements along the y-axis shown in blue. Consider a plane orthogonal to the ULA axis at the origin. The broadside angle, β, is the angle between the plane and the signal direction. To compute the broadside angle, construct a line from any point on the signal path to the plane, orthogonal to the plane. The angle between these two lines is the broadside angle and lies in the interval [–90°,90°]. The broadside angle is positive when measured toward the positive direction of the array axis. When β is zero, the signal path is orthogonal to the array axis. When β = ±90, the signal path lies along the array axis. All signal paths having the same broadside angle form a cone around the ULA axis.

The conversion from azimuth angle, az, and elevation angle, el, to broadside angle, β, is
This equation shows that
For an elevation angle of zero, the broadside angle equals the azimuth angle.
Elevation angles equally above and below the xy plane result in identical broadside angles.
You can convert from broadside angle to azimuth angle but you must specify the elevation angle
Because the signals paths for a given broadside angle, β, form a cone around the array axis, you cannot specify the elevation angle arbitrarily. The elevation angle and broadside angle must satisfy
As an example, the figure below shows a ULA with elements spaced d meters apart along the y-axis. The ULA is illuminated by a plane wave emitted from a point source in the far field. Choose the azimuth angle to be 90°. Then the signal direction lies in the yz-plane and satisfies sinβ = cos(el). The broadside angle is the complement of the elevation angle.
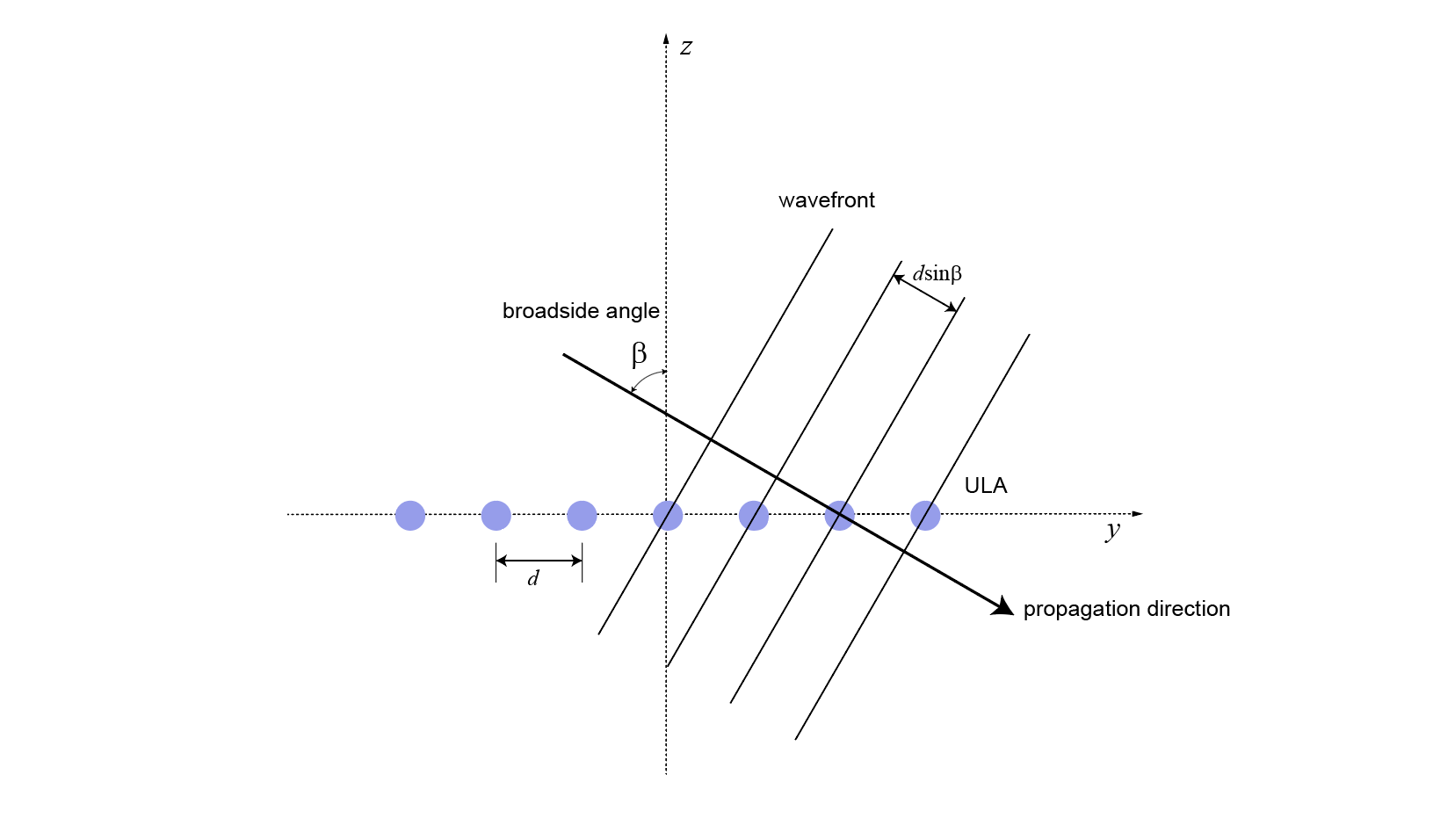
Because of the angle of arrival, the array elements are not simultaneously illuminated by the plane wave. The additional distance the incident wave travels between array elements is d sinβ where d is the distance between array elements. The constant time delay, τ, between array elements is
where c is the speed of the wave.
For broadside angles of ±90°, the signal is incident on the array parallel to the array axis and the time delay between sensors equals ±d/c. For a broadside angle of zero, the plane wave illuminates all elements of the ULA simultaneously and the time delay between elements is zero.
Phased Array System Toolbox software provides functions az2broadside and broadside2az for
converting between azimuth and broadside angles.
Convert Between Broadside Angles and Azimuth and Elevation
The following examples show how to use the az2broadside and broadside2az functions.
A target is located at an azimuth angle of 45° and at an elevation angle of 60° relative to a ULA. Determine the corresponding broadside angle.
bsang = az2broadside(45,60)
bsang = 20.7048
Calculate the azimuth for an incident signal arriving at a broadside angle of 45° and an elevation of 20°.
az = broadside2az(45,20)
az = 48.8063