pmtm
Multitaper power spectral density estimate
Syntax
Description
pxx = pmtm(x)pxx, of the
input signal x using Discrete Prolate Spheroidal (Slepian) Sequences as tapers.
pxx = pmtm(x,m,'Tapers','sine')
[___] = pmtm(___,
returns the multitaper PSD estimate over the frequency range specified by
freqrange)freqrange.
[___,
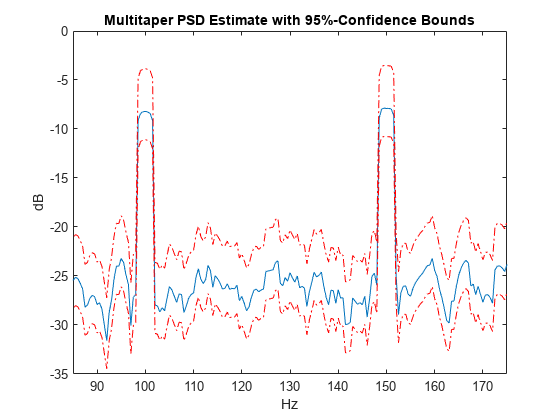
returns the pxxc] = pmtm(___,'ConfidenceLevel',probability)probability × 100% confidence intervals for the PSD
estimate in pxxc.
[___] = pmtm(___,'DropLastTaper',
specifies whether dropflag)pmtm drops the last Slepian taper when computing the
multitaper PSD estimate.
[___] = pmtm(___,
combines the individual tapered PSD estimates using the method specified in
method)method. This syntax applies only to Slepian tapers.
[___] = pmtm(
uses the cell array x,dpss_params,___)dpss_params to pass input arguments to
dpss. This syntax applies only to Slepian tapers.
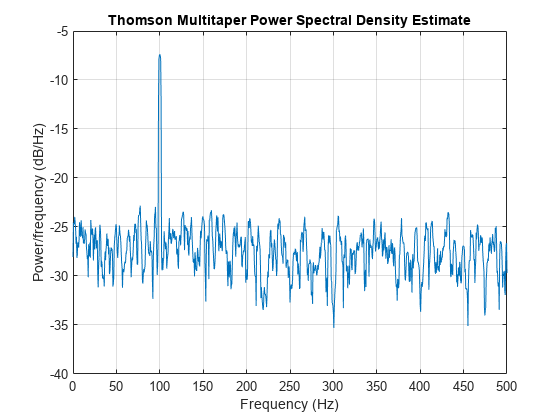
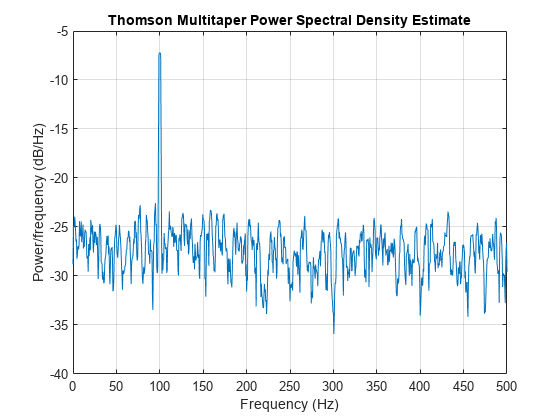
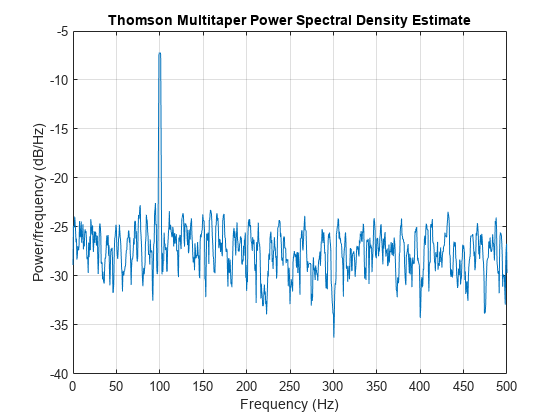
pmtm(___) with no output arguments plots the multitaper
PSD estimate in the current figure window.
Examples
Input Arguments
Output Arguments
More About
References
[1] McCoy, Emma J., Andrew T. Walden, and Donald B. Percival. "Multitaper Spectral Estimation of Power Law Processes." IEEE® Transactions on Signal Processing 46, no. 3 (March 1998): 655–68. https://doi.org/10.1109/78.661333.
[2] Percival, Donald B., and Andrew T. Walden. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge; New York, NY, USA: Cambridge University Press, 1993.
[3] Riedel, Kurt S., and Alexander Sidorenko. “Minimum Bias Multiple Taper Spectral Estimation.” IEEE Transactions on Signal Processing 43, no. 1 (January 1995): 188–95. https://doi.org/10.1109/78.365298.
[4] Thomson, David J. "Spectrum estimation and harmonic analysis." Proceedings of the IEEE 70, no. 9 (1982): 1055–96. https://doi.org/10.1109/PROC.1982.12433.
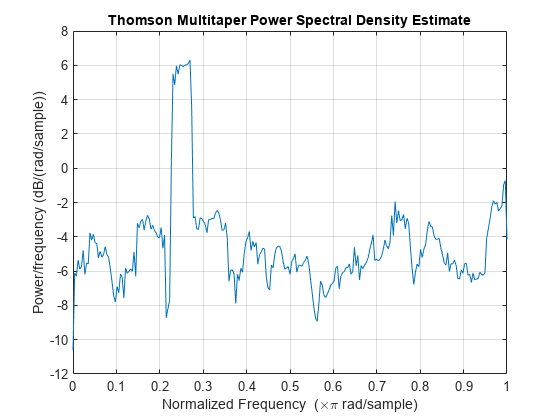
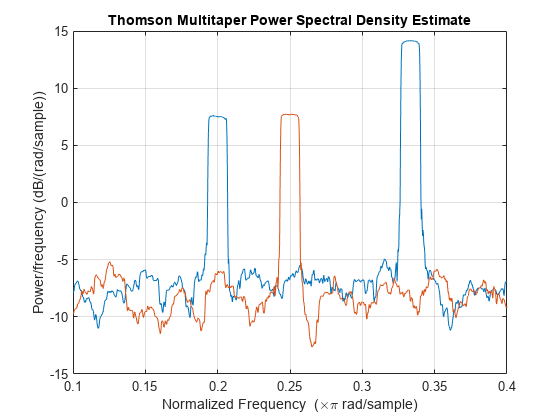
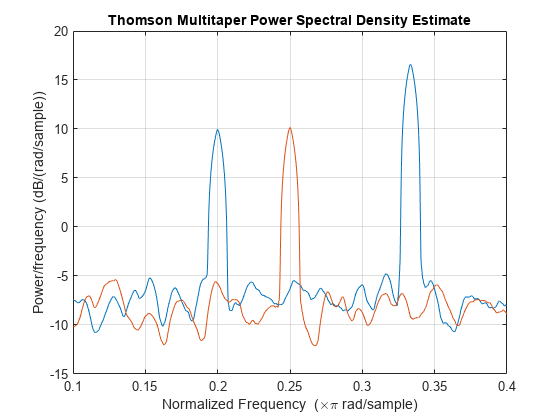
![Figure contains an axes object. The axes object with title Proportion of Energy in [-w,w] of k-th Slepian Sequence contains an object of type stem.](../../examples/signal/win64/DPSSSequencesAndTheirFrequencyDomainConcentrationsExample_01.png)
![Figure contains an axes object. The axes object with title Proportion of Energy in [-w,w] of k-th Slepian Sequence contains 2 objects of type stem, line.](../../examples/signal/win64/DPSSSequencesAndTheirFrequencyDomainConcentrationsExample_02.png)