La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Équations différentielles à retard

Solveurs de problèmes de valeur initiale pour les équations différentielles à retard

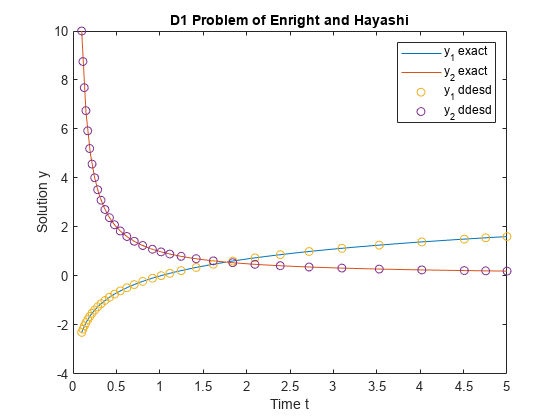
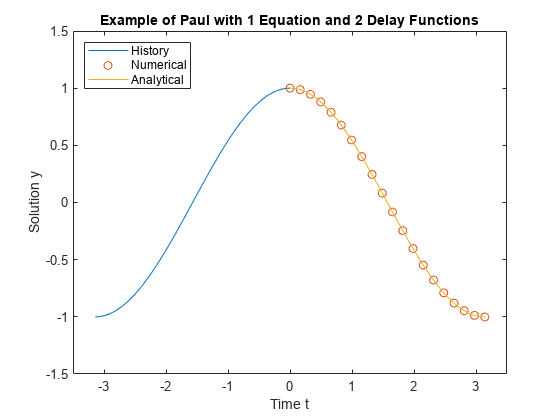
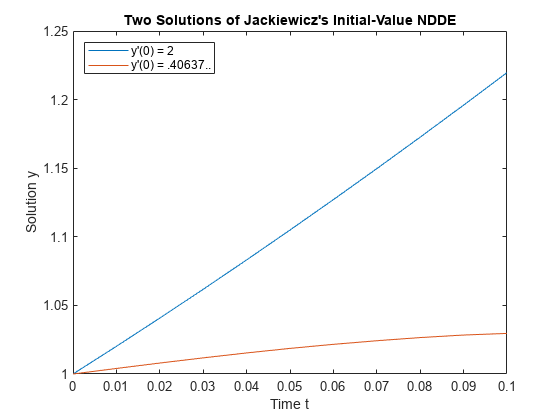
Les équations différentielles à retard (DDE) contiennent des termes dont la valeur dépend de la solution obtenue aux instants précédents. Les retards peuvent être constants, dépendants du temps ou dépendants de l’état. Le choix de la fonction de solveur (dde23, ddesd ou ddensd) dépend du type de retards dans l’équation. En général, le retard lie la valeur de la dérivée actuelle à la valeur de la solution à un instant précédent. Mais dans le cas d’une équation neutre, il peut la lier à la valeur de la dérivée aux instants précédents. Puisque les équations dépendent de la solution obtenue aux instants précédents, il est nécessaire d’inclure une fonction historique qui transmet la valeur de la solution avant l’instant initial t₀. Pour plus d’informations, consultez Solving Delay Differential Equations.

Plotted solutions of two delay differential equation problems

Fonctions

développer tout

Solveurs

`dde23`	Solve delay differential equations (DDEs) with constant delays
`ddesd`	Solve delay differential equations (DDEs) with general delays
`ddensd`	Solve delay differential equations (DDEs) of neutral type

Obtenir/Définir les options

`ddeget`	Extract properties from delay differential equations options structure
`ddeset`	Create or alter delay differential equations options structure

Évaluer la solution

deval Evaluate differential equation solution structure

Rubriques

Solving Delay Differential Equations
Background information, solver capabilities and algorithms, and example summary.
DDE with Constant Delays
This example shows how to use dde23 to solve a system of DDEs (delay differential equations) with constant delays.
DDE with State-Dependent Delays
This example shows how to use ddesd to solve a system of DDEs (delay differential equations) with state-dependent delays.
Cardiovascular Model DDE with Discontinuities
This example shows how to use dde23 to solve a cardiovascular model that has a discontinuous derivative.
DDE of Neutral Type
This example shows how to use ddensd to solve a neutral DDE (delay differential equation), where delays appear in derivative terms.
Initial Value DDE of Neutral Type
This example shows how to use ddensd to solve a system of initial value DDEs (delay differential equations) with time-dependent delays.