spectrogram
Spectrogram using short-time Fourier transform
Syntax
Description
s = spectrogram(x)x. Each column of
s contains an estimate of the short-term,
time-localized frequency content of x. The magnitude
squared of s is known as the
spectrogram time-frequency representation of
x
[1].
[___,
also returns a matrix, ps] = spectrogram(___,spectrumtype)ps, proportional to the spectrogram
of x.
If you specify
spectrumtypeas"psd", each column ofpscontains an estimate of the power spectral density (PSD) of a windowed segment.If you specify
spectrumtypeas"power", each column ofpscontains an estimate of the power spectrum of a windowed segment.
[___] = spectrogram(___,"reassigned") reassigns
each PSD or power spectrum estimate to the location of its center of energy. If
your signal contains well-localized temporal or spectral components, then this
option generates a sharper spectrogram.
[___] = spectrogram(___,
returns the PSD or power spectrum estimate over the frequency range specified by
freqrange)freqrange. Valid options for
freqrange are "onesided",
"twosided", and "centered".
[___] = spectrogram(___,
specifies additional options using name-value arguments. Options include the
minimum threshold and output time dimension.Name=Value)
Examples
Generate samples of a signal that consists of a sum of sinusoids. The normalized frequencies of the sinusoids are rad/sample and rad/sample. The higher frequency sinusoid has 10 times the amplitude of the other sinusoid.
N = 1024; n = 0:N-1; w0 = 2*pi/5; x = sin(w0*n)+10*sin(2*w0*n);
Compute the short-time Fourier transform using the function defaults. Plot the spectrogram.
s = spectrogram(x);
spectrogram(x,'yaxis')
Repeat the computation.
Divide the signal into sections of length .
Window the sections using a Hamming window.
Specify 50% overlap between contiguous sections.
To compute the FFT, use points, where .
Verify that the two approaches give identical results.
Nx = length(x); nsc = floor(Nx/4.5); nov = floor(nsc/2); nff = max(256,2^nextpow2(nsc)); t = spectrogram(x,hamming(nsc),nov,nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
Divide the signal into 8 sections of equal length, with 50% overlap between sections. Specify the same FFT length as in the preceding step. Compute the short-time Fourier transform and verify that it gives the same result as the previous two procedures.
ns = 8; ov = 0.5; lsc = floor(Nx/(ns-(ns-1)*ov)); t = spectrogram(x,lsc,floor(ov*lsc),nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
Generate a signal that consists of a complex-valued convex quadratic chirp sampled at 600 Hz for 2 seconds. The chirp has an initial frequency of 250 Hz and a final frequency of 50 Hz.
fs = 6e2; ts = 0:1/fs:2; x = chirp(ts,250,ts(end),50,"quadratic",0,"convex","complex");
spectrogram Function
Use the spectrogram function to compute the STFT of the signal.
Divide the signal into segments, each samples long.
Specify samples of overlap between adjoining segments.
Discard the final, shorter segment.
Window each segment with a Bartlett window.
Evaluate the discrete Fourier transform of each segment at points. By default,
spectrogramcomputes two-sided transforms for complex-valued signals.
M = 49; L = 11; g = bartlett(M); Ndft = 1024; [s,f,t] = spectrogram(x,g,L,Ndft,fs);
Use the waterplot function to compute and display the spectrogram, defined as the magnitude squared of the STFT.
waterplot(s,f,t)

STFT Definition
Compute the STFT of the -sample signal using the definition. Divide the signal into overlapping segments. Window each segment and evaluate its discrete Fourier transform at points.
segs = framesig(1:length(x),M,OverlapLength=L); X = fft(x(segs).*g,Ndft);
Compute the time and frequency ranges for the STFT.
To find the time values, divide the time vector into overlapping segments. The time values are the midpoints of the segments, with each segment treated as an interval open at the lower end.
To find the frequency values, specify a Nyquist interval closed at zero frequency and open at the lower end.
framedT = ts(segs); tint = mean(framedT(2:end,:)); fint = 0:fs/Ndft:fs-fs/Ndft;
Compare the output of spectrogram to the definition. Display the spectrogram.
maxdiff = max(max(abs(s-X)))
maxdiff = 0
waterplot(X,fint,tint)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Generate a signal consisting of a chirp sampled at 1.4 kHz for 2 seconds. The frequency of the chirp decreases linearly from 600 Hz to 100 Hz during the measurement time.
fs = 1400; x = chirp(0:1/fs:2,600,2,100);
stft Defaults
Compute the STFT of the signal using the spectrogram and stft functions. Use the default values of the stft function:
Divide the signal into 128-sample segments and window each segment with a periodic Hann window.
Specify 96 samples of overlap between adjoining segments. This length is equivalent to 75% of the window length.
Specify 128 DFT points and center the STFT at zero frequency, with the frequency expressed in hertz.
Verify that the two results are equal.
M = 128; g = hann(M,"periodic"); L = 0.75*M; Ndft = 128; [sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered"); [s,f,t] = stft(x,fs); dff = max(max(abs(sp-s)))
dff = 0
Use the mesh function to plot the two outputs.
nexttile mesh(tp,fp,abs(sp).^2) title("spectrogram") view(2), axis tight nexttile mesh(t,f,abs(s).^2) title("stft") view(2), axis tight

spectrogram Defaults
Repeat the computation using the default values of the spectrogram function:
Divide the signal into segments of length , where is the length of the signal. Window each segment with a Hamming window.
Specify 50% overlap between segments.
To compute the FFT, use points. Compute the spectrogram only for positive normalized frequencies.
M = floor(length(x)/4.5); g = hamming(M); L = floor(M/2); Ndft = max(256,2^nextpow2(M)); [sx,fx,tx] = spectrogram(x); [st,ft,tt] = stft(x,Window=g,OverlapLength=L, ... FFTLength=Ndft,FrequencyRange="onesided"); dff = max(max(sx-st))
dff = 0
Use the waterplot function to plot the two outputs. Divide the frequency axis by in both cases. For the stft output, divide the sample numbers by the effective sample rate, .
figure nexttile waterplot(sx,fx/pi,tx) title("spectrogram") nexttile waterplot(st,ft/pi,tt/(2*pi)) title("stft")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency/\pi") ylabel("Samples") end
Use the spectrogram function to measure and track the instantaneous frequency of a signal.
Generate a quadratic chirp sampled at 1 kHz for two seconds. Specify the chirp so that its frequency is initially 100 Hz and increases to 200 Hz after one second.
fs = 1000;
t = 0:1/fs:2-1/fs;
y = chirp(t,100,1,200,'quadratic');Estimate the spectrum of the chirp using the short-time Fourier transform implemented in the spectrogram function. Divide the signal into sections of length 100, windowed with a Hamming window. Specify 80 samples of overlap between adjoining sections and evaluate the spectrum at frequencies.
spectrogram(y,100,80,100,fs,'yaxis')
Track the chirp frequency by finding the time-frequency ridge with highest energy across the time points. Overlay the instantaneous frequency on the spectrogram plot.
[~,f,t,p] = spectrogram(y,100,80,100,fs); [fridge,~,lr] = tfridge(p,f); hold on plot3(t,fridge,abs(p(lr)),'LineWidth',4) hold off

Generate 512 samples of a chirp with sinusoidally varying frequency content.
N = 512; n = 0:N-1; x = exp(1j*pi*sin(8*n/N)*32);
Compute the centered two-sided short-time Fourier transform of the chirp. Divide the signal into 32-sample segments with 16-sample overlap. Specify 64 DFT points. Plot the spectrogram.
[scalar,fs,ts] = spectrogram(x,32,16,64,'centered'); spectrogram(x,32,16,64,'centered','yaxis')

Obtain the same result by computing the spectrogram on 64 equispaced frequencies over the interval . The 'centered' option is not necessary.
fintv = -pi+pi/32:pi/32:pi;
[vector,fv,tv] = spectrogram(x,32,16,fintv);
spectrogram(x,32,16,fintv,'yaxis')
Generate a signal that consists of a voltage-controlled oscillator and three Gaussian atoms. The signal is sampled at kHz for 2 seconds.
fs = 2000; tx = 0:1/fs:2; gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A'; s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5; x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs); x = s+x';
Short-Time Fourier Transforms
Use the pspectrum function to compute the STFT.
Divide the -sample signal into segments of length samples, corresponding to a time resolution of milliseconds.
Specify samples or 20% of overlap between adjoining segments.
Window each segment with a Kaiser window and specify a leakage .
M = 80; L = 16; lk = 0.7; [S,F,T] = pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk);
Compare to the result obtained with the spectrogram function.
Specify the window length and overlap directly in samples.
pspectrumalways uses a Kaiser window as . The leakage and the shape factor of the window are related by .pspectrumalways uses points when computing the discrete Fourier transform. You can specify this number if you want to compute the transform over a two-sided or centered frequency range. However, for one-sided transforms, which are the default for real signals,spectrogramuses points. Alternatively, you can specify the vector of frequencies at which you want to compute the transform, as in this example.If a signal cannot be divided exactly into segments,
spectrogramtruncates the signal whereaspspectrumpads the signal with zeros to create an extra segment. To make the outputs equivalent, remove the final segment and the final element of the time vector.spectrogramreturns the STFT, whose magnitude squared is the spectrogram.pspectrumreturns the segment-by-segment power spectrum, which is already squared but is divided by a factor of before squaring.For one-sided transforms,
pspectrumadds an extra factor of 2 to the spectrogram.
g = kaiser(M,40*(1-lk)); k = (length(x)-L)/(M-L); if k~=floor(k) S = S(:,1:floor(k)); T = T(1:floor(k)); end [s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);
Use the waterplot function to display the spectrograms computed by the two functions.
subplot(2,1,1) waterplot(sqrt(S),F,T) title("pspectrum") subplot(2,1,2) waterplot(s,f,t) title("spectrogram")

maxd = max(max(abs(abs(s).^2-S)))
maxd = 2.4419e-08
Power Spectra and Convenience Plots
The spectrogram function has a fourth argument that corresponds to the segment-by-segment power spectrum or power spectral density. Similar to the output of pspectrum, the ps argument is already squared and includes the normalization factor . For one-sided spectrograms of real signals, you still have to include the extra factor of 2. Set the scaling argument of the function to "power".
[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");
max(abs(S(:)-ps(:)))ans = 2.4419e-08
When called with no output arguments, both pspectrum and spectrogram plot the spectrogram of the signal in decibels. Include the factor of 2 for one-sided spectrograms. Set the colormaps to be the same for both plots. Set the x-limits to the same values to make visible the extra segment at the end of the pspectrum plot. In the spectrogram plot, display the frequency on the y-axis.
subplot(2,1,1) pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk) title("pspectrum") cc = clim; xl = xlim; subplot(2,1,2) spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis") title("spectrogram") clim(cc) xlim(xl)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Generate a chirp signal sampled for 2 seconds at 1 kHz. Specify the chirp so that its frequency is initially 100 Hz and increases to 200 Hz after 1 second.
fs = 1000;
t = 0:1/fs:2;
y = chirp(t,100,1,200,"quadratic");Estimate the reassigned spectrogram of the signal.
Divide the signal into sections of length 128, windowed with a Kaiser window with shape parameter .
Specify 120 samples of overlap between adjoining sections.
Evaluate the spectrum at frequencies and time bins.
Use the spectrogram function with no output arguments to plot the reassigned spectrogram. Display frequency on the y-axis and time on the x-axis.
spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned","yaxis")

Redo the plot using the imagesc function. Specify the y-axis direction so that the frequency values increase from bottom to top. Add eps to the reassigned spectrogram to avoid potential negative infinities when converting to decibels.
[~,fr,tr,pxx] = spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned"); imagesc(tr,fr,pow2db(pxx+eps)) axis xy xlabel("Time (s)") ylabel("Frequency (Hz)") colorbar

Generate a chirp signal sampled for 2 seconds at 1 kHz. Specify the chirp so that its frequency is initially 100 Hz and increases to 200 Hz after 1 second.
Fs = 1000;
t = 0:1/Fs:2;
y = chirp(t,100,1,200,'quadratic');Estimate the time-dependent power spectral density (PSD) of the signal.
Divide the signal into sections of length 128, windowed with a Kaiser window with shape parameter .
Specify 120 samples of overlap between adjoining sections.
Evaluate the spectrum at frequencies and time bins.
Output the frequency and time of the center of gravity of each PSD estimate. Set to zero those elements of the PSD smaller than dB.
[~,~,~,pxx,fc,tc] = spectrogram(y,kaiser(128,18),120,128,Fs, ... 'MinThreshold',-30);
Plot the nonzero elements as functions of the center-of-gravity frequencies and times.
plot(tc(pxx>0),fc(pxx>0),'.')
Generate a signal that consists of a real-valued chirp sampled at 2 kHz for 2 seconds.
fs = 2000;
tx = 0:1/fs:2;
x = vco(-chirp(tx,0,tx(end),2).*exp(-3*(tx-1).^2), ...
[0.1 0.4]*fs,fs).*hann(length(tx))';Two-Sided Spectrogram
Compute and plot the two-sided STFT of the signal.
Divide the signal into segments, each samples long.
Specify samples of overlap between adjoining segments.
Discard the final, shorter segment.
Window each segment with a flat-top window.
Evaluate the discrete Fourier transform of each segment at points, noting that it is an odd number.
M = 73;
L = 24;
g = flattopwin(M);
Ndft = 895;
neven = ~mod(Ndft,2);
[stwo,f,t] = spectrogram(x,g,L,Ndft,fs,"twosided");Use the spectrogram function with no output arguments to plot the two-sided spectrogram.
spectrogram(x,g,L,Ndft,fs,"twosided","power","yaxis")

Compute the two-sided spectrogram using the definition. Divide the signal into -sample segments with samples of overlap between adjoining segments. Window each segment and compute its discrete Fourier transform at points.
y = framesig(x,M,Window=g,OverlapLength=L); Xtwo = fft(y,Ndft);
Compute the time and frequency ranges.
To find the time values, divide the time vector into overlapping segments. The time values are the midpoints of the segments, with each segment treated as an interval open at the lower end.
To find the frequency values, specify a Nyquist interval closed at zero frequency and open at the upper end.
framedT = framesig(tx,M,OverlapLength=L); ttwo = mean(framedT(2:end,:)); ftwo = 0:fs/Ndft:fs*(1-1/Ndft);
Compare the outputs of spectrogram to the definitions. Use the waterplot function to display the spectrograms.
diffs = [max(max(abs(stwo-Xtwo)));
max(abs(f-ftwo'));
max(abs(t-ttwo))]diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xtwo,ftwo,ttwo) title("Two-Sided, Definition") nexttile waterplot(stwo,f,t) title("Two-Sided, spectrogram Function")

Centered Spectrogram
Compute the centered spectrogram of the signal.
Use the same time values that you used for the two-sided STFT.
Use the
fftshiftfunction to shift the zero-frequency component of the STFT to the center of the spectrum.For odd-valued , the frequency interval is open at both ends. For even-valued , the frequency interval is open at the lower end and closed at the upper end.
Compare the outputs and display the spectrograms.
tcen = ttwo; if ~neven Xcen = fftshift(Xtwo,1); fcen = -fs/2*(1-1/Ndft):fs/Ndft:fs/2; else Xcen = fftshift(circshift(Xtwo,-1),1); fcen = (-fs/2*(1-1/Ndft):fs/Ndft:fs/2)+fs/Ndft/2; end [scen,f,t] = spectrogram(x,g,L,Ndft,fs,"centered"); diffs = [max(max(abs(scen-Xcen))); max(abs(f-fcen')); max(abs(t-tcen))]
diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xcen,fcen,tcen) title("Centered, Definition") nexttile waterplot(scen,f,t) title("Centered, spectrogram Function")

One-Sided Spectrogram
Compute the one-sided spectrogram of the signal.
Use the same time values that you used for the two-sided STFT.
For odd-valued , the one-sided STFT consists of the first rows of the two-sided STFT. For even-valued , the one-sided STFT consists of the first rows of the two-sided STFT.
For odd-valued , the frequency interval is closed at zero frequency and open at the Nyquist frequency. For even-valued , the frequency interval is closed at both ends.
Compare the outputs and display the spectrograms. For real-valued signals, the "onesided" argument is optional.
tone = ttwo; if ~neven Xone = Xtwo(1:(Ndft+1)/2,:); else Xone = Xtwo(1:Ndft/2+1,:); end fone = 0:fs/Ndft:fs/2; [sone,f,t] = spectrogram(x,g,L,Ndft,fs); diffs = [max(max(abs(sone-Xone))); max(abs(f-fone')); max(abs(t-tone))]
diffs = 3×1
10-12 ×
0
0.1137
0.0002
figure nexttile waterplot(Xone,fone,tone) title("One-Sided, Definition") nexttile waterplot(sone,f,t) title("One-Sided, spectrogram Function")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
The spectrogram function has a matrix containing either the power spectral density (PSD) or the power spectrum of each segment as the fourth output argument. The power spectrum is equal to the PSD multiplied by the equivalent noise bandwidth (ENBW) of the window.
Generate a signal that consists of a logarithmic chirp sampled at 1 kHz for 1 second. The chirp has an initial frequency of 400 Hz that decreases to 10 Hz by the end of the measurement.
fs = 1000;
tt = 0:1/fs:1-1/fs;
y = chirp(tt,400,tt(end),10,"logarithmic");Segment PSDs and Power Spectra with Sample Rate
Divide the signal into 102-sample segments and window each segment with a Hann window. Specify 12 samples of overlap between adjoining segments and 1024 DFT points.
M = 102; g = hann(M); L = 12; Ndft = 1024;
Compute the spectrogram of the signal with the default PSD spectrum type. Output the STFT and the array of segment power spectral densities.
[s,f,t,p] = spectrogram(y,g,L,Ndft,fs);
Repeat the computation with the spectrum type specified as "power". Output the STFT and the array of segment power spectra.
[r,~,~,q] = spectrogram(y,g,L,Ndft,fs,"power");Verify that the spectrogram is the same in both cases. Plot the spectrogram using a logarithmic scale for the frequency.
max(max(abs(s).^2-abs(r).^2))
ans = 0
waterfall(f,t,abs(s)'.^2) set(gca,XScale="log",... XDir="reverse",View=[30 50])

Verify that the power spectra are equal to the power spectral densities multiplied by the ENBW of the window.
max(max(abs(q-p*enbw(g,fs))))
ans = 1.1102e-16
Verify that the matrix of segment power spectra is proportional to the spectrogram. The proportionality factor is the square of the sum of the window elements.
max(max(abs(s).^2-q*sum(g)^2))
ans = 0
Segment PSDs and Power Spectra with Normalized Frequencies
Repeat the computation, but now work in normalized frequencies. The results are the same when you specify the sample rate as .
[~,~,~,pn] = spectrogram(y,g,L,Ndft);
[~,~,~,qn] = spectrogram(y,g,L,Ndft,"power");
max(max(abs(qn-pn*enbw(g,2*pi))))ans = 1.1102e-16
Load an audio signal that contains two decreasing chirps and a wideband splatter sound. Compute the short-time Fourier transform. Divide the waveform into 400-sample segments with 300-sample overlap. Plot the spectrogram.
load splat % To hear, type soundsc(y,Fs) sg = 400; ov = 300; spectrogram(y,sg,ov,[],Fs,"yaxis") colormap bone

Use the spectrogram function to output the power spectral density (PSD) of the signal.
[s,f,t,p] = spectrogram(y,sg,ov,[],Fs);
Track the two chirps using the medfreq function. To find the stronger, low-frequency chirp, restrict the search to frequencies above 100 Hz and to times before the start of the wideband sound.
f1 = f > 100; t1 = t < 0.75; m1 = medfreq(p(f1,t1),f(f1));
To find the faint high-frequency chirp, restrict the search to frequencies above 2500 Hz and to times between 0.3 seconds and 0.65 seconds.
f2 = f > 2500; t2 = t > 0.3 & t < 0.65; m2 = medfreq(p(f2,t2),f(f2));
Overlay the result on the spectrogram. Divide the frequency values by 1000 to express them in kHz.
hold on plot(t(t1),m1/1000,LineWidth=4) plot(t(t2),m2/1000,LineWidth=4) hold off

Generate two seconds of a signal sampled at 10 kHz. Specify the instantaneous frequency of the signal as a triangular function of time.
fs = 10e3; t = 0:1/fs:2; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*fs,fs);
Compute and plot the spectrogram of the signal. Use a Kaiser window of length 256 and shape parameter . Specify 220 samples of section-to-section overlap and 512 DFT points. Plot the frequency on the y-axis. Use the default colormap and view.
spectrogram(x1,kaiser(256,5),220,512,fs,'yaxis')
Change the view to display the spectrogram as a waterfall plot. Set the colormap to bone.
view(-45,65)
colormap bone
Since R2025a
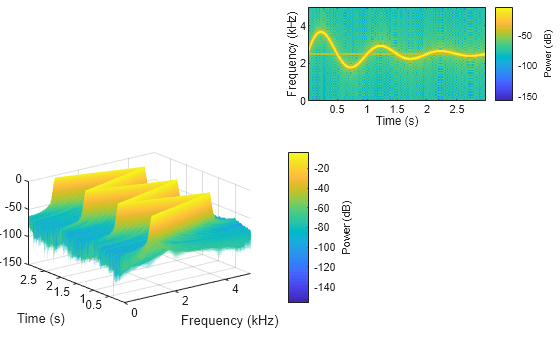
Plot the spectrograms for four signals in axes handles and panel containers. When you use spectrogram without output arguments, the function returns a convenience plot with the power spectral density (PSD) estimate. To reproduce this plot on a specific axes handle or panel container, specify spectrogram with a target Parent input argument.
Create four oscillating signals with a sample rate of 10 kHz for three seconds.
x1: Sawtooth-shaped oscillating signalx2: Exponentially decaying oscillating signalx3: Complex sinusoidal envelopex4: Quadratic-sweeping chirp
Fs = 10e3; t = 0:1/Fs:3; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs); x2 = vco(sin(2*pi*t).*exp(-t),[0.1 0.4]*Fs,Fs) ... + 0.01*sin(2*pi*0.25*Fs*t); x3 = exp(1j*pi*sin(4*t)*Fs/10); x4 = chirp(t,Fs/10,t(end),Fs/2.5,"quadratic");
Define specifications to calculate the signal spectrograms: 512 DFT points, a 256-sample Kaiser window, and an overlap length of 220 samples.
nfft = 512; g = kaiser(256,5); ol = 220;
Plot Spectrograms in Axes Handle
Create two axes handles in the southwestern and northeastern corners of a new figure window.
fig = figure; ax1 = axes(fig,Position=[0.05 0.1 0.55 0.45]); ax2 = axes(fig,Position=[0.55 0.7 0.42 0.28]);
Plot the power spectra of the signals x1 and x2 in the southwestern and northeastern axes of the figure, respectively. View the spectrogram of x1 in the default 3-D line of sight. Display the frequencies in the y-axis for the spectrogram of x2.
spectrogram(x1,g,ol,nfft,Fs,"power",Parent=ax1); view(ax1,3); spectrogram(x2,g,ol,nfft,Fs,"power","yaxis",Parent=ax2);
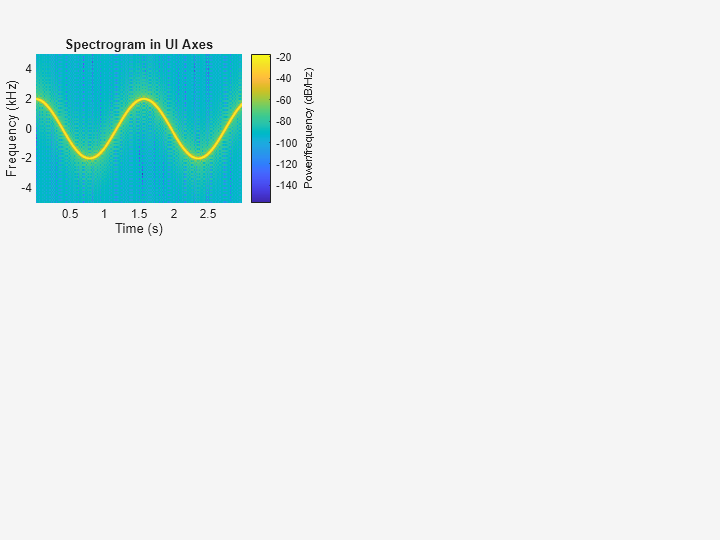
Plot Spectrogram in UI-based Axes Handle
Create an axes handle in the northwestern corner of a new UI figure window.
uif = uifigure(Position=[100 100 720 540]);
ax3 = uiaxes(uif,'Position',[5 305 300 200]);Plot the PSD estimate of the signal x3 on the figure axes. Display the frequencies in the y-axis and centered in 0 kHz.
spectrogram(x3,g,ol,nfft,Fs,"centered","yaxis",Parent=ax3); title(ax3,"Spectrogram in UI Axes")
Plot Spectrogram in Panel Container
Add a panel container in the southeastern corner of the UI figure window.
ax4 = uipanel(uif,Position=[300 5 400 325], ... Title="Spectrogram in UI Panel", ... BackgroundColor="white");
Plot the PSD estimate of the signal x4 on the panel container. Display the frequencies in the y-axis.
spectrogram(x4,g,ol,nfft,Fs,"yaxis",Parent=ax4);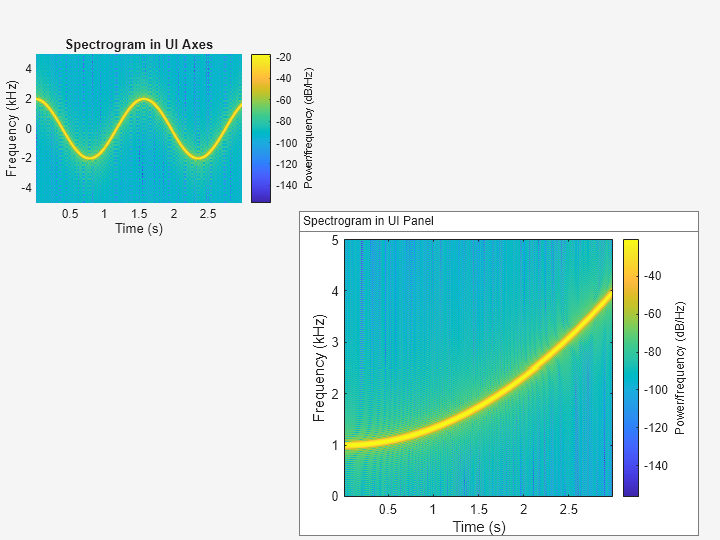
Input Arguments
Input signal, specified as a row or column vector.
Example: cos(pi/4*(0:159))+randn(1,160) specifies a
sinusoid embedded in white Gaussian noise.
Data Types: single | double
Complex Number Support: Yes
Window, specified as a positive integer or as a row or column vector. Use
window to divide the signal into segments:
If
windowis an integer, thenspectrogramdividesxinto segments of lengthwindowand windows each segment with a Hamming window of that length.If
windowis a vector, thenspectrogramdividesxinto segments of the same length as the vector and windows each segment usingwindow.
If the length of x cannot be divided
exactly into an integer number of segments with
noverlap overlapping samples, then
x is truncated accordingly.
If you specify window as empty, then
spectrogram uses a Hamming window such that
x is divided into eight segments with
noverlap overlapping samples.
For a list of available windows, see Windows.
Example: hann(N+1) and
(1-cos(2*pi*(0:N)'/N))/2 both specify a Hann window
of length N + 1.
Number of overlapped samples, specified as a nonnegative integer.
If
windowis scalar, thennoverlapmust be smaller thanwindow.If
windowis a vector, thennoverlapmust be smaller than the length ofwindow.
If you specify noverlap as empty, then
spectrogram uses a number that produces 50% overlap
between segments. If the segment length is unspecified, the function sets
noverlap to ⌊Nx/4.5⌋, where Nx is the
length of the input signal and the ⌊⌋ symbols denote the floor function.
Number of DFT points, specified as a positive integer scalar. If you
specify nfft as empty, then
spectrogram sets the parameter to max(256,2p), where p = ⌈log2 Nw⌉, the ⌈⌉ symbols denote the ceiling function, and
Nw =
windowifwindowis a scalar.Nw =
length(ifwindow)windowis a vector.
Normalized frequencies, specified as a vector. w must
have at least two elements, because otherwise the function interprets it as
nfft. Normalized frequencies are in
rad/sample.
Example: pi./[2 4]
Data Types: single | double
Sample rate, specified as a positive scalar. The sample rate is the number of samples per unit time. If the unit of time is seconds, then the sample rate is in Hz.
Frequency range for the PSD estimate, specified as
"onesided", "twosided", or
"centered". For real-valued signals, the default is
"onesided". For complex-valued signals, the default
is "twosided", and specifying
"onesided" results in an error.
"onesided"— returns the one-sided spectrogram of a real input signal. Ifnfftis even, thenpshasnfft/2 + 1 rows and is computed over the interval [0, π] rad/sample. Ifnfftis odd, thenpshas (nfft+ 1)/2 rows and the interval is [0, π) rad/sample. If you specifyfs, then the intervals are respectively [0,fs/2] cycles/unit time and [0,fs/2) cycles/unit time."twosided"— returns the two-sided spectrogram of a real or complex-valued signal.pshasnfftrows and is computed over the interval [0, 2π) rad/sample. If you specifyfs, then the interval is [0,fs) cycles/unit time."centered"— returns the centered two-sided spectrogram of a real or complex-valued signal.pshasnfftrows. Ifnfftis even, thenpsis computed over the interval (–π, π] rad/sample. Ifnfftis odd, thenpsis computed over (–π, π) rad/sample. If you specifyfs, then the intervals are respectively (–fs/2,fs/2] cycles/unit time and (–fs/2,fs/2) cycles/unit time.
Data Types: char | string
Power spectrum scaling, specified as "psd" or
"power".
Omitting
spectrumtype, or specifying"psd", returns the power spectral density.Specifying
"power"scales each estimate of the PSD by the equivalent noise bandwidth of the window. The result is an estimate of the power at each frequency. If the"reassigned"option is on, the function integrates the PSD over the width of each frequency bin before reassigning.
Data Types: char | string
Frequency display axis, specified as "xaxis" or
"yaxis".
"xaxis"— displays frequency on the x-axis and time on the y-axis."yaxis"— displays frequency on the y-axis and time on the x-axis.
This argument is ignored if you call
spectrogram with output arguments.
Data Types: char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: spectrogram(x,100,OutputTimeDimension="downrows")
divides x into segments of length 100 and windows each segment
with a Hamming window of that length The output of the spectrogram has time
dimension down the rows.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: spectrogram(x,100,'OutputTimeDimension','downrows')
divides x into segments of length 100 and windows each segment
with a Hamming window of that length The output of the spectrogram has time
dimension down the rows.
Threshold, specified as a real scalar expressed in decibels.
spectrogram sets to zero those elements of
s such that
10 log10(s) ≤ thresh.
Output time dimension, specified as "acrosscolumns"
or "downrows". Set this value to
"downrows", if you want the time dimension of
s, ps,
fc, and tc down the rows
and the frequency dimension along the columns. Set this value to
"acrosscolumns", if you want the time dimension
of s, ps,
fc, and tc across the
columns and frequency dimension along the rows. This input is ignored if
the function is called without output arguments.
Data Types: char | string
Since R2025a
Target parent, specified as an Axes
object, UIAxes
object, or Panel object.
If you specify
Parent, thespectrogramfunction plots the PSD or power spectrum as a surface plot on the specified target parent. The function returns the plot even if you call it with or without output arguments.If you do not specify
Parentand you do not specify output arguments, thespectrogramfunction plots the PSD or power spectrum as a surface plot on the current axes or chart thatgcareturns.
For more information about targets, see Graphics Objects. For more information about the parent-child relationship in MATLAB® graphics, see Graphics Object Hierarchy.
Data Types: Axes | UIAxes | Panel
Output Arguments
Short-time Fourier transform, returned as a matrix. Time increases across
the columns of s and frequency increases down the rows,
starting from zero.
Note
When freqrange is set to
"onesided", spectrogram
outputs the s values in the positive Nyquist
range and does not conserve the total power.
s is not affected by the
"reassigned" option.
Time instants, returned as a vector. The time values in
t correspond to the midpoint of each
segment.
Power spectral density (PSD) or power spectrum, returned as a matrix.
If
xis real andfreqrangeis left unspecified or set to"onesided", thenpscontains the one-sided modified periodogram estimate of the PSD or power spectrum of each segment. The function multiplies the power by 2 at all frequencies except 0 and the Nyquist frequency to conserve the total power.If
xis complex-valued or iffreqrangeis set to"twosided"or"centered", thenpscontains the two-sided modified periodogram estimate of the PSD or power spectrum of each segment.If you specify a vector of normalized frequencies in
wor a vector of cyclical frequencies inf, thenpscontains the modified periodogram estimate of the PSD or power spectrum of each segment evaluated at the input frequencies.
Center-of-energy frequencies and times, returned as matrices of the same
size as the short-time Fourier transform. If you do not specify a sample
rate, then the elements of fc are returned as normalized
frequencies.
More About
The short-time Fourier transform (STFT) is used to analyze how the frequency content of a nonstationary signal changes over time. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal. For more information about the spectrogram and how to compute it using Signal Processing Toolbox™ functions, see Spectrogram Computation with Signal Processing Toolbox.
The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has
columns, where Nx is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals NDFT, the number of DFT points, for centered and two-sided transforms and an odd number close to NDFT/2 for one-sided transforms of real-valued signals.
The mth column of the STFT matrix contains the DFT of the windowed data centered about time mR:
Tips
If a short-time Fourier transform has zeros, its conversion
to decibels results in negative infinities that cannot be plotted.
To avoid this potential difficulty, spectrogram adds eps to
the short-time Fourier transform when you call it with no output arguments.
References
[1] Boashash, Boualem, ed. Time Frequency Signal Analysis and Processing: A Comprehensive Reference. Second edition. EURASIP and Academic Press Series in Signal and Image Processing. Amsterdam and Boston: Academic Press, 2016.
[2] Chassande-Motin, Éric, François Auger, and Patrick Flandrin. "Reassignment." In Time-Frequency Analysis: Concepts and Methods. Edited by Franz Hlawatsch and François Auger. London: ISTE/John Wiley and Sons, 2008.
[3] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.
[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. Second edition. Upper Saddle River, NJ: Prentice Hall, 1999.
[5] Rabiner, Lawrence R., and Ronald W. Schafer. Digital Processing of Speech Signals. Englewood Cliffs, NJ: Prentice-Hall, 1978.
Extended Capabilities
The
spectrogram function supports tall arrays with the following usage
notes and limitations:
Input must be a tall column vector.
The
windowargument must always be specified.OutputTimeDimensionmust be always specified and set to"downrows".The
reassignedoption is not supported.Syntaxes with no output arguments are not supported.
For more information, see Tall Arrays.
Usage notes and limitations:
The
Parentinput argument is not supported.Arguments specified using name-value arguments must be compile-time constants.
Usage notes and limitations:
Arguments specified using name-value arguments must be compile-time constants.
Variable-size
windowmust be double precision.
Usage notes and limitations:
The syntax with no output arguments is not supported.
The frequency vector must be uniformly spaced.
For more information, see Run MATLAB Functions in Thread-Based Environment.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006aThe spectrogram function supports single-precision
variable-size window inputs for code generation.
The spectrogram function supports single-precision inputs and
code generation for graphical processing units (GPUs). You must have MATLAB
Coder™ and GPU Coder™ to generate CUDA® code.
You can now use the Create
Plot Live Editor task to visualize the output of
spectrogram interactively. You can select different chart
types and set optional parameters. The task also automatically generates code that
becomes part of your live script.
See Also
Apps
Functions
goertzel|istft|periodogram|pspectrum|pwelch|stft|xspectrogram
Topics
External Websites
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)