Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

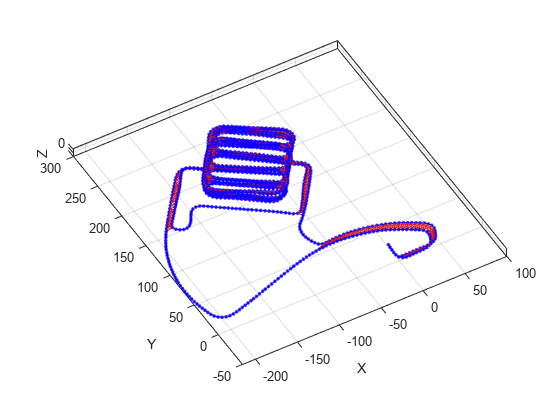
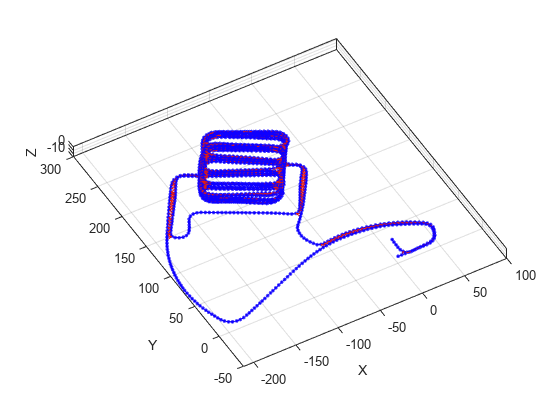
optimizePoseGraph

Optimiser les nœuds dans le graphique de pose

Depuis R2019b

Syntaxe

updatedGraph = optimizePoseGraph(poseGraph)

updatedGraph = optimizePoseGraph(poseGraph,solver)

[updatedGraph,solutionInfo] = optimizePoseGraph(___)

[___] = optimizePoseGraph(___,Name,Value)

Description

updatedGraph = optimizePoseGraph(poseGraph) ajuste les poses en fonction de leurs contraintes de bord définies dans le graphique spécifié pour améliorer le graphique global. Vous optimisez un graphique de pose 2D ou 3D. Le graphique de pose renvoyé a la même topologie avec des nœuds mis à jour.

Cette optimisation du graphe de pose suppose que toutes les contraintes de bord et les fermetures de boucles sont valides. Pour envisager de couper les bords en fonction de mauvaises fermetures de boucles, consultez la fonction trimLoopClosures .

updatedGraph = optimizePoseGraph(poseGraph,solver) spécifie le type de solveur pour optimiser le graphe de pose.

[updatedGraph,solutionInfo] = optimizePoseGraph(___) renvoie des statistiques supplémentaires sur le processus d'optimisation dans solutionInfo en utilisant l'une des syntaxes précédentes.

[___] = optimizePoseGraph(___,Name,Value) spécifie des options supplémentaires en utilisant une ou plusieurs paires Name,Value . Par exemple, 'MaxIterations',1000 augmente le nombre maximum d’itérations à 1 000.

Exemples

Optimiser un graphique de pose 3D

Optimisez un graphique de pose en fonction des nœuds et des contraintes de bord. Le graphique de pose utilisé dans cet exemple est tiré du MIT Dataset et a été généré à partir des informations extraites d'un parking.

Chargez le graphique de pose à partir de l'ensemble de données MIT. Inspectez l'objet poseGraph3D pour afficher le nombre de nœuds et de fermetures de boucle.

load parking-garage-posegraph.mat pg
disp(pg);

  poseGraph3D with properties:

               NumNodes: 1661
               NumEdges: 6275
    NumLoopClosureEdges: 4615
     LoopClosureEdgeIDs: [128 129 130 132 133 134 135 137 138 139 140 142 143 144 146 147 148 150 151 204 205 207 208 209 211 212 213 215 216 217 218 220 221 222 223 225 226 227 228 230 231 232 233 235 236 237 238 240 241 242 243 244 ... ] (1x4615 double)
        LandmarkNodeIDs: [1x0 double]

Tracez le graphique de pose sans les identifiants. Les lignes rouges indiquent les fermetures de boucles identifiées dans l'ensemble de données.

title('Original Pose Graph')
show(pg,'IDs','off');
view(-30,45)

Optimisez le graphique de pose. Les nœuds sont ajustés en fonction des contraintes de bord et des fermetures de boucles. Tracez le graphique de pose optimisé pour voir l'ajustement des nœuds avec des fermetures de boucle.

updatedPG = optimizePoseGraph(pg);
figure
title('Updated Pose Graph')
show(updatedPG,'IDs','off');
view(-30,45)

Arguments d'entrée

poseGraph — Graphique de pose 2D ou 3D

poseGraph objet | poseGraph3D objet | Objet digraph

Graphique de pose 2D ou 3D, spécifié comme objet poseGraph, poseGraph3D, digraph .

Pour utiliser l'objet digraph , générez le graphique de pose en utilisant createPoseGraph à partir d'un imageviewset ou pcviewset. . Vous devez avoir Computer Vision Toolbox™ et le solver doit être défini sur "builtin-trust-region". Les paires nom-valeur 'LoopClosuresToIgnore' et 'FirstNodePose' sont ignorées si elles sont spécifiées.

Les bords de l'objet digraph sont décrits par les objets simtform3d (Image Processing Toolbox) ou rigidtform3d (Image Processing Toolbox) .

solver — Solveur de graphiques de pose

"builtin-trust-region" (par défaut) | "g2o-levenberg-marquardt"

Solveur de graphique de pose, spécifié comme "builtin-trust-region" ou "g2o-levenberg-marquardt". Pour régler l'un ou l'autre solveur, utilisez les arguments de la paire nom-valeur pour ce solveur.

Arguments nom-valeur

Spécifiez des paires d'arguments facultatives sous la forme Name1=Value1,...,NameN=ValueN, où Name est le nom de l'argument et Value est la valeur correspondante. Les arguments nom-valeur doivent apparaître après les autres arguments, mais l'ordre des paires n'a pas d'importance.

Avant R2021a, utilisez des virgules pour séparer chaque nom et valeur, et mettez Name entre guillemets.

Exemple : 'MaxTime', 300

Remarque

En fonction de l'entrée solver , la fonction prend en charge différentes paires nom-valeur.

Si l'entrée solver est définie sur "builtin-trust-region":

MaxTime — Durée maximale autorisée

500 (par défaut) | scalaire numérique positif

Temps maximum autorisé, spécifié sous la forme d'une paire séparée par des virgules composée de 'MaxTime' et d'un scalaire numérique positif en secondes. L'optimiseur se ferme après avoir dépassé ce délai.

GradientTolerance — Limite inférieure de la norme de gradient

0.5e-8 (par défaut) | scalaire

Limite inférieure de la norme du gradient, spécifiée comme la paire séparée par des virgules composée de 'GradientTolerance' et d'un scalaire. La norme du gradient est calculée en fonction de la fonction de coût de l'optimisation. Si la norme tombe en dessous de cette valeur, l'optimiseur se ferme.

FunctionTolerance — Limite inférieure de la variation de la fonction de coût

1e-8 (par défaut) | scalaire

Limite inférieure de la modification de la fonction de coût, spécifiée comme la paire séparée par des virgules composée de 'FunctionTolerance' et d'un scalaire. Si la modification de la fonction de coût tombe en dessous de cette valeur entre les étapes d'optimisation, l'optimiseur se termine.

StepTolerance — Limite inférieure de la taille du pas

1e-12 (par défaut) | scalaire

Limite inférieure de la taille du pas, spécifiée comme la paire séparée par des virgules composée de 'StepTolerance' et d'un scalaire. Si la norme de l'étape d'optimisation tombe en dessous de cette valeur, l'optimiseur se termine.

InitialTrustRegionRadius — Rayon initial de la région de confiance

100 (par défaut) | scalaire

Rayon initial de la région de confiance, spécifié sous forme de scalaire.

VerboseOutput — Afficher les informations sur l'itération intermédiaire

'off' (par défaut) | 'on'

Afficher les informations d'itération intermédiaire sur la ligne de commande MATLAB^® , spécifiées comme une paire séparée par des virgules composée de 'VerboseOutput' et soit 'off' ou 'on'.

LoopClosuresToIgnore — ID des bords de fermeture de boucle dans le graphique de pose

vecteur

ID des bords de fermeture de boucle dans poseGraph, spécifiés comme la paire séparée par des virgules composée de 'LoopClosuresToIgnore' et d'un vecteur. Pour obtenir les identifiants de bord du graphique de pose, utilisez findEdgeID.

FirstNodePose — Pose du premier nœud

[0 0 0] ou [0 0 0 1 0 0 0] (par défaut) | [x y theta] | [x y z qw qx qy qz]

Pose du premier nœud dans poseGraph, spécifiée comme la paire séparée par des virgules composée de 'FirstNodePose' et d'un vecteur de pose.

Pour poseGraph (2-D), la pose est un vecteur [x y theta] , qui définit la position relative xy-position et l'angle d'orientation, theta.

Pour poseGraph3D, la pose est un vecteur [x y z qw qx qy qz] , qui définit la position relative xyz et l'orientation du quaternion, [qw qx qy qz].

Remarque

De nombreuses autres sources de graphiques de pose 3D, y compris les formats .g2o , spécifient l'orientation du quaternion dans un ordre différent, par exemple, [qx qy qz qw]. Vérifiez la source de vos données de graphique de pose avant d'ajouter des nœuds à votre objet poseGraph3D .

Si l'entrée solver est définie sur "g2o-levenberg-marquardt":

MaxIterations — Nombre maximum d'itérations

300 (par défaut) | entier positif

Nombre maximal d'itérations, spécifié sous la forme d'une paire séparée par des virgules composée de 'MaxIterations' et d'un entier positif. L'optimiseur se ferme après avoir dépassé ce nombre d'itérations.

MaxTime — Durée maximale autorisée

500 (par défaut) | scalaire numérique positif

Temps maximum autorisé, spécifié sous la forme d'une paire séparée par des virgules composée de 'MaxTime' et d'un scalaire numérique positif en secondes. L'optimiseur se ferme après avoir dépassé ce délai.

FunctionTolerance — Limite inférieure de la variation de la fonction de coût

1e-8 (par défaut) | scalaire

Limite inférieure de la modification de la fonction de coût, spécifiée comme la paire séparée par des virgules composée de 'FunctionTolerance' et d'un scalaire. Si la modification de la fonction de coût tombe en dessous de cette valeur entre les étapes d'optimisation, l'optimiseur se termine.

VerboseOutput — Afficher les informations sur l'itération intermédiaire

'off' (par défaut) | 'on'

Afficher les informations d'itération intermédiaire sur la ligne de commande MATLAB , spécifiées comme une paire séparée par des virgules composée de 'VerboseOutput' et soit 'off' ou 'on'.

LoopClosuresToIgnore — ID des bords de fermeture de boucle dans le graphique de pose

vecteur

ID des bords de fermeture de boucle dans poseGraph, spécifiés comme la paire séparée par des virgules composée de 'LoopClosuresToIgnore' et d'un vecteur. Pour obtenir les identifiants de bord du graphique de pose, utilisez findEdgeID.

FirstNodePose — Pose du premier nœud

[0 0 0] ou [0 0 0 1 0 0 0] (par défaut) | [x y theta] | [x y z qw qx qy qz]

Pose du premier nœud dans poseGraph, spécifiée comme la paire séparée par des virgules composée de 'FirstNodePose' et d'un vecteur de pose.

Pour poseGraph (2-D), la pose est un vecteur [x y theta] , qui définit la position relative xy-position et l'angle d'orientation, theta.

Pour poseGraph3D, la pose est un vecteur [x y z qw qx qy qz] , qui définit la position relative xyz et l'orientation du quaternion, [qw qx qy qz].

Remarque

De nombreuses autres sources de graphiques de pose 3D, y compris les formats .g2o , spécifient l'orientation du quaternion dans un ordre différent, par exemple, [qx qy qz qw]. Vérifiez la source de vos données de graphique de pose avant d'ajouter des nœuds à votre objet poseGraph3D .

Arguments de sortie

updatedGraph — Graphique de pose 2D ou 3D optimisé

poseGraph objet | poseGraph3D objet

Graphique de pose 2D ou 3D optimisé, renvoyé sous la forme d'un objet poseGraph ou poseGraph3D .

solutionInfo — Statistiques du processus d'optimisation

structure

Statistiques du processus d'optimisation, renvoyées sous forme de structure avec ces champs :

• Iterations — Nombre d'itérations utilisées dans l'optimisation.

• ResidualError — Valeur de la fonction de coût à la fermeture de l'optimiseur.

• Exit Flag — Condition de sortie pour l'optimiseur :

  • 1 — Minimum local trouvé.

  • 2 — Nombre maximum d'itérations atteint. Voir l'argument de paire nom-valeur MaxIterations .

  • 3 — L'algorithme a expiré pendant le fonctionnement.

  • 4 — Taille de pas minimale. La taille du pas est inférieure à l'argument de la paire nom-valeur StepTolerance .

  • 5 — La variation de l'erreur est inférieure au minimum.

  • 8 — Le rayon de la région de confiance est inférieur au minimum défini dans InitialTrustRegionRadius.

Références

[1] Grisetti, G., R. Kummerle, C. Stachniss, and W. Burgard. "A Tutorial on Graph-Based SLAM." IEEE Intelligent Transportation Systems Magazine. Vol. 2, No. 4, 2010, pp. 31–43. doi:10.1109/mits.2010.939925.

[2] Carlone, Luca, Roberto Tron, Kostas Daniilidis, and Frank Dellaert. "Initialization Techniques for 3D SLAM: a Survey on Rotation Estimation and its Use in Pose Graph Optimization." 2015 IEEE International Conference on Robotics and Automation (ICRA). 2015, pp. 4597–4604.

Capacités étendues

Génération de code C/C++

Générez du code C et C++ avec MATLAB® Coder™.

• Utilisez cette syntaxe lors de la construction d'objets poseGraph ou poseGraph3D pour la génération de code :

  poseGraph = poseGraph('MaxNumEdges',maxEdges,'MaxNumNodes',maxNodes) spécifie une limite supérieure sur le nombre d'arêtes et de nœuds autorisés dans le graphe de pose lors de la génération du code. Cette limite n'est requise que lors de la génération de code.

• L'argument d'entrée "g2o-levenberg-marquardt" solver n'est pas pris en charge pour la génération de code.

Historique des versions

Introduit dans R2019b

Voir aussi

Fonctions

• trimLoopClosures | addRelativePose | removeEdges | edgeNodePairs | edgeConstraints | findEdgeID | nodeEstimates

Objets

• poseGraph | poseGraph3D | lidarSLAM

Rubriques

• Implement Simultaneous Localization And Mapping (SLAM) with Lidar Scans
• Implement Online Simultaneous Localization And Mapping (SLAM) with Lidar Scans