zpk
Modèle zéro-pôle-gain
Description
Utilisez zpk pour créer des modèles zéro-pôle-gain ou pour convertir des modèles de systèmes dynamiques en modèles zéro-pôle-gain.
Les modèles zéro-pôle-gain représentent les fonctions de transfert sous forme factorisée. Par exemple, considérons la fonction de transfert SISO en temps continu suivante :
G(s) peut être factorisée sous la forme zéro-pôle-gain comme suit :
Une représentation plus générale du modèle SISO zéro-pôle-gain est la suivante :
Ici, z et p sont les vecteurs des zéros et des pôles à valeurs réelles ou complexes, et k est le gain scalaire à valeurs réelles ou complexes. Pour les modèles MIMO, chaque canal d'E/S est représenté par une fonction de transfert de ce type hij(s).
Vous pouvez créer un objet de modèle zéro-pôle-gain en spécifiant directement les pôles, zéros et gains ou en convertissant un modèle d’un autre type (tel qu’un modèle de représentation d’état ss) en modèle zéro-pôle-gain.
Vous pouvez également utiliser zpk pour créer des modèles de représentation d’état généralisés (genss) ou incertains (uss (Robust Control Toolbox)).
Création
Syntaxe
Description
Créer un modèle ZPK
sys = zpk(zeros,poles,gain)zeros et poles spécifiés comme des vecteurs et la valeur scalaire de gain. La sortie sys obtenue est un objet modèle zpk stockant les données du modèle. Réglez zeros ou poles sur [] pour les systèmes sans zéros ni pôles. Ces deux entrées n’ont pas besoin de présenter la même longueur et le modèle n’a pas à être correct (autrement dit avoir un excès de pôles).
sys = zpk(___,PropertyName=Value)
Convertir en modèle ZPK
sys = zpk(ltiSys,Name=Value)zpk tronquée du modèle parcimonieux ltiSys en calculant les zéros et les pôles sur la base d’un ou plusieurs arguments nom-valeur spécifiés. Puisque cette méthode calcule les zéros pour chaque paire d’entrée-sortie, elle convient mieux aux modèles ayant de petites tailles d’entrées-sorties. (depuis R2025a)
Créer une variable pour une expression rationnelle
s = zpk('s') crée une variable spéciale s que vous pouvez utiliser dans une expression rationnelle pour créer un modèle zéro-pôle-gain en temps continu. Il est parfois plus aisé et plus intuitif de recourir à une expression rationnelle plutôt que de spécifier des coefficients polynomiaux.
Arguments en entrée
Zéros du modèle zéro-pôle-gain, spécifiés comme suit :
Vecteur ligne de modèles SISO. Par exemple, utilisez
[1,2+i,2-i]pour créer un modèle avec des zéros às = 1,s = 2+iets = 2-i. Pour un exemple, voir Modèle SISO zéro-pôle-gain en temps continu.Cell array
NyparNude vecteurs ligne servant à spécifier un modèle MIMO zéro-pôle-gain oùNydésigne le nombre de sorties etNu, le nombre d’entrées. Pour un exemple, voir Modèle MIMO zéro-pôle-gain en temps discret.
Par exemple, si a est un paramètre realp réglable présentant la valeur nominale 3, vous pouvez utiliser zeros = [1 2 a] pour créer un modèle genss avec des zéros à s = 1 et s = 2 et un zéro réglable à s = 3.
Lorsque vous utilisez cet argument d'entrée pour créer un modèle zpk, l'argument définit la valeur initiale de la propriété Z.
Pôles du modèle zéro-pôle-gain, spécifiés comme suit :
Vecteur ligne de modèles SISO. Pour un exemple, voir Modèle SISO zéro-pôle-gain en temps continu.
Cell array
NyparNude vecteurs ligne servant à spécifier un modèle MIMO zéro-pôle-gain oùNydésigne le nombre de sorties etNu, le nombre d’entrées. Pour un exemple, voir Modèle MIMO zéro-pôle-gain en temps discret.
Définissez également une propriété de l’objet zpk. Cet argument d’entrée définit la valeur de la propriété P.
Gain du modèle zéro-pôle-gain, spécifié comme suit :
Scalaire pour modèles SISO. Pour un exemple, voir Modèle SISO zéro-pôle-gain en temps continu.
Matrice
NyparNuservant à spécifier un modèle MIMO zéro-pôle-gain oùNydésigne le nombre de sorties etNu, le nombre d’entrées. Pour un exemple, voir Modèle MIMO zéro-pôle-gain en temps discret.
Définissez également une propriété de l’objet zpk. Cet argument d’entrée définit la valeur de la propriété K.
Pas d’échantillonnage spécifié en tant que scalaire. Définissez également une propriété de l’objet zpk. Cet argument d’entrée définit la valeur de la propriété Ts.
Système dynamique spécifié en tant que modèle de système dynamique SISO or MIMO ou en tant que tableau de modèles de systèmes dynamiques. Parmi les systèmes dynamiques que vous pouvez utiliser, citons :
Modèles LTI numériques en temps continu ou discret, tels que les modèles
tf,zpk,ssoupid.Si
ltiSysest un modèle de représentation d’état parcimonieux (sparssoumechss), le logiciel calcule une approximation zéro-pôle-gain tronquée dans une bande de fréquence d’attention spécifiée. Pour les modèles parcimonieux, utilisez les arguments nom-valeur pour spécifier les options de calcul. Si vous ne spécifiez aucune option, le logiciel calcule jusqu’aux 1 000 premiers pôles et zéros avec la plus petite amplitude. De plus, obtenir une approximation zéro-pôle-gain tronquée est applicable uniquement pour les modèles ayant une représentationsparssvalide. (depuis R2025a)Modèles LTI généralisés ou incertains tels que les modèles
genssouuss(Robust Control Toolbox). (Pour pouvoir utiliser les modèles incertains, une licence Robust Control Toolbox™ est nécessaire.)Le modèle zéro-pôle-gain obtenu s'appuie sur :
les valeurs actuelles des composants réglables pour les blocs de design de systèmes de contrôle réglables.
les valeurs de modèle nominales pour les blocs de design de systèmes de contrôle incertains.
Modèles LTI identifiés tels que les modèles
idtf(System Identification Toolbox),idss(System Identification Toolbox),idproc(System Identification Toolbox),idpoly(System Identification Toolbox) etidgrey(System Identification Toolbox). Pour sélectionner la composante du modèle identifié à convertir, spécifiezcomponent. Si vous ne spécifiez pascomponent,tfconvertit la composante mesurée du modèle identifié par défaut. (Pour pouvoir utiliser les modèles identifiés, le software System Identification Toolbox™ est nécessaire)Un modèle non linéaire identifié ne peut pas être converti en objet modèle
zpk. Vous pouvez commencer par utiliser des fonctions d'approximation linéaire telles quelinearizeetlinapp(Cette fonctionnalité nécessite le software System Identification Toolbox.)
Gain statique spécifié en tant que scalaire ou matrice. Le gain statique ou le gain à l'état stable d’un système représente le rapport sortie/entrée en présence d’un état stable.
Composante du modèle identifié à convertir, spécifiée sous l’une des formes suivantes :
'measured': convertit la composante mesurée desys.'noise': convertit la composante de bruit desys'augmented': convertit à la fois la composante mesurée et la composante de bruit desys.
component ne s’applique que lorsque sys est un modèle LTI identifié.
Pour plus d’informations sur les modèles LTI identifiés et leurs composantes mesurée et de bruit, voir Identified LTI Models.
Arguments nom-valeur
Spécifiez des paires d’arguments optionnelles sous la forme Name1=Value1,...,NameN=ValueN, où Name est le nom de l’argument et Value est la valeur correspondante. Les arguments nom-valeur doivent apparaître après les autres arguments, mais l’ordre des paires n’a pas d’importance.
Exemple : sys = zpk(sparseSys,Focus=[0 100],Display="off")
Depuis R2025a
Utilisez le calcul parallèle pendant le calcul des pôles et des zéros, spécifié sous la forme numérique ou logique 0 (false) ou 1 (true).
Quand UseParallel est défini sur true, vous pouvez choisir explicitement de mettre à l’échelle de votre environnement parallèle privilégié. Activer le calcul parallèle peut se traduire par une performance améliorée pendant le calcul des zéros et des pôles. Cependant, même avec UseParallel défini sur false, l’algorithme peut utiliser le multithreading prédéfini pour utiliser les ressources locales de manière optimale. Pour plus d’informations, consultez MATLAB Multicore.
Cette option nécessite une licence Parallel Computing Toolbox™.
Depuis R2025a
Pente d’atténuation, spécifiée en tant que scalaire non positif ou matrice.
Utilisez une valeur scalaire pour les modèles SISO ou quand la pente est uniforme pour toutes les paires d’entrée-sortie pour les modèles MIMO.
Utilisez une matrice quand la pente est différente pour chaque paire d’entrée-sortie pour les modèles MIMO.
Cette option vous permet de spécifier comment l’approximation devrait décroître après la plage de fréquences spécifiée. Par exemple, Slope de -2 garantit la décroissance du gain à une vitesse d’au moins –40 dB/décade (la vitesse d’atténuation de 1/s2) au-delà de fmax.
Depuis R2025a
Plage de fréquences d’intérêt, spécifiée en tant que vecteur de forme [0,fmax]. Quand vous spécifiez une plage de fréquences d’attention, le logiciel ne calcule que les pôles à fréquence naturelle dans cette plage. Pour les modèles en temps discret, le logiciel estime la fréquence naturelle équivalente via la transformation de Tustin.
Puisque zpk calcule tous les pôles et zéros dans la plage de fréquences spécifiée, vous spécifiez généralement une plage basse fréquence pour éviter de calculer un grand nombre de pôles et de zéros. Par défaut, l’attention est non spécifiée ([0 Inf]) et l’algorithme calcule jusqu’à MaxNumber pôles et zéros.
Depuis R2025a
Nombre maximal de pôles et de zéros à calculer, spécifié en tant qu’entier positif. Cette valeur limite le nombre de pôles et de zéros calculés par l’algorithme et l’ordre d’approximation du modèle parcimonieux original.
Depuis R2025a
Décalage spectral, spécifié en tant que scalaire fini.
Le logiciel calcule les pôles avec la fréquence naturelle dans la plage spécifiée [0,fmax] au moyen d’itérations de puissance inverse pour A-sigma*E, ce qui obtient les valeurs propres les plus proches du décalage sigma. Quand A est singulier et sigma est zéro, l’algorithme échoue car aucune inverse n’existe. Par conséquent, pour les modèles parcimonieux avec action intégrale (s = 0 ou à z = 1 pour les modèles en temps discret), vous pouvez utiliser cette option pour décaler implicitement des pôles ou des zéros à la valeur la plus proche de cette valeur de décalage. Spécifiez une valeur de décalage qui n’est pas égale à une valeur existante de pôle ou de zéro du modèle original.
Depuis R2025a
Tolérance pour la précision des pôles et des zéros calculés, spécifiée en tant que scalaire fini positif. Cette valeur contrôle la convergence des valeurs propres calculées dans les itérations de puissance inverse.
Depuis R2025a
Afficher ou masquer un rapport d’avancement, spécifié en tant que "off" ou "on".
Arguments en sortie
Modèle de système en sortie renvoyé sous la forme suivante :
Un objet de modèle zéro-pôle-gain (
zpk), lorsque les arguments d'entréezeros,polesetgaincontiennent des valeurs numériques.sysest toujours un objet de modèlezpklors de la conversion deltiSysen type de modèlezpk.Un modèle de représentation d’état généralisé (
genss) lorsque les arguments d’entréezeros,polesetgaincomprennent des paramètres réglables, tels que les paramètresrealpou les matrices généralisées (genmat).Un modèle de représentation d’état incertain (
uss) lorsque les arguments d’entréezerospolesetgaincomprennent des paramètres incertains. Pour pouvoir utiliser les modèles incertains, une licence Robust Control Toolbox est nécessaire.
Propriétés
Zéros du système, spécifiés comme suit :
Cell array des zéros de la fonction de transfert ou des racines du numérateur pour les modèles SISO.
Cell array
NyparNude vecteurs ligne des zéros pour chaque paire d’E/S d’un modèle MIMO oùNydésigne le nombre de sorties etNu, le nombre d’entrées.
Les valeurs du Z peuvent présenter des valeurs réelles ou complexes.
Pôles du système, spécifiés comme suit :
Cell array des pôles de la fonction de transfert ou des racines du dénominateur pour les modèles SISO.
Cell array
NyparNude vecteurs ligne des pôles pour chaque paire d’E/S d’un modèle MIMO oùNydésigne le nombre de sorties etNu, le nombre d’entrées.
Les valeurs du P peuvent présenter des valeurs réelles ou complexes.
Gains du système, spécifiés comme suit :
Valeur scalaire pour modèles SISO.
Matrice
NyparNustockant les valeurs de gain pour chaque paire d’E/S d’un modèle MIMO oùNydésigne le nombre de sorties etNu, le nombre d’entrées.
Les valeurs du K peuvent présenter des valeurs réelles ou complexes.
Spécifie le mode de factorisation des polynômes numérateur et dénominateur pour l'affichage, spécifiés de l’une des manières suivantes :
'roots': affiche les facteurs en termes d'emplacement des racines du polynôme.'roots'correspond à la valeur par défaut deDisplayFormat.'frequency': affiche les facteurs en termes de fréquences naturelles de la racine ω0 et d'amortissement ζ.Le format d'affichage
'frequency'n'est pas disponible pour les modèles en temps discret avec la valeurVariable'z^-1'ou'q^-1'.'time constant': affiche les facteurs en termes de constantes de temps de la racine τ0 et d'amortissement ζ.Le format d'affichage
'time constant'n'est pas disponible pour les modèles en temps discret avec la valeurVariable'z^-1'ou'q^-1'.
Pour les modèles en temps continu, le tableau suivant indique la manière dont les facteurs polynomiaux sont disposés dans chaque format d'affichage.
Valeur DisplayName | Facteur de premier ordre (racine réelle ) | Facteur de deuxième ordre (paire de racines complexes ) |
|---|---|---|
'roots' | où | |
'frequency' | où | où |
'time constant' | où | où |
Pour les modèles en temps discret, les facteurs polynomiaux sont agencés de la même manière que pour les modèles en temps continu, avec les substitutions de variables suivantes :
où Ts correspond au pas d'échantillonnage. En temps discret, τ et ω0 correspondent étroitement à la constante de temps et à la fréquence naturelle de la racine équivalente en temps continu, pour autant que la condition suivante soit remplie : .
Variable d’affichage du modèle zéro-pôle-gain, spécifiée sous l’une des formes suivantes :
's': valeur par défaut des modèles en temps continu'z': valeur par défaut des modèles en temps discret'p': équivalent de's''q': équivalent de'z''z^-1': inverse de'z''q^-1': équivalent de'z^-1'
Retard de transport spécifié sous l’une des formes suivantes :
Scalaire : spécifiez le retard de transport pour un système SISO ou le même retard de transport pour toutes les paires entrée/sortie d'un système MIMO.
Tableau
NyparNu: spécifiez des retards de transport distincts pour chaque paire entrée/sortie d'un système MIMO. Ici,Nydésigne le nombre de sorties etNu, le nombre d’entrées.
Pour les systèmes en temps continu, spécifiez les retards de transport dans l'unité temporelle spécifiée par la propriété TimeUnit. Pour les systèmes en temps discret, spécifiez les retards de transport en tant qu’entiers multiples du pas d’échantillonnage, Ts. Pour plus d'informations sur le retard, consultez Time Delays in Linear Systems.
Retard en entrée pour chaque canal d’entrée spécifié sous l’une des formes suivantes :
Scalaire : spécifiez le retard en entrée pour un système SISO ou le même retard pour toutes les entrées d'un système à entrées multiples.
Vecteur
Nupar 1 : spécifiez des retards d’entrée distincts pour l’entrée d’un système à entrées multiples oùNudésigne le nombre d’entrées.
Pour les systèmes en temps continu, spécifiez les retards en entrée dans l'unité temporelle spécifiée par la propriété TimeUnit. Pour les systèmes en temps discret, spécifiez les retards en entrée en tant qu’entiers multiples du pas d’échantillonnage, Ts.
Pour plus d’informations, consultez Time Delays in Linear Systems.
Retard en sortie pour chaque canal de sortie spécifié sous l’une des formes suivantes :
Scalaire : spécifiez le retard en sortie pour un système SISO ou le même retard pour toutes les sorties d'un système à sorties multiples.
Vecteur
Nypar 1 : spécifiez des retards de sortie distincts pour la sortie d’un système à sorties multiples oùNydésigne le nombre de sorties.
Pour les systèmes en temps continu, spécifiez les retards en sortie dans l'unité temporelle spécifiée par la propriété TimeUnit. Pour les systèmes en temps discret, spécifiez les retards en sortie en tant qu’entiers multiples du pas d’échantillonnage, Ts.
Pour plus d’informations, consultez Time Delays in Linear Systems.
Pas d’échantillonnage spécifié en tant que :
0pour les systèmes en temps continu.Scalaire positif représentant la période d’échantillonnage d’un système en temps discret. Spécifiez
Tsdans l'unité temporelle définie par la propriétéTimeUnit.-1pour un système en temps discret avec un pas d’échantillonnage non spécifié.
Unités temporelles variables spécifiées sous l’une des formes suivantes :
'nanoseconds''microseconds''milliseconds''seconds''minutes''hours''days''weeks''months''years'
La modification de TimeUnit n’a aucune incidence sur les autres propriétés mais change l’ensemble du comportement du système. Utilisez chgTimeUnit pour faire des conversions entre les unités temporelles sans modifier le comportement du système.
Noms des canaux en entrée spécifiés sous l'une des formes suivantes :
Vecteur de caractères pour les modèles à entrée unique.
Cell array de vecteurs de caractères pour les modèles à entrées multiples.
'', pas de nom spécifié pour les canaux en entrée.
Sinon, vous pouvez attribuer des noms aux entrées pour les modèles à entrées multiples au moyen de l'expansion vectorielle automatique. Par exemple, si sys est un modèle à deux entrées, saisissez ce qui suit :
sys.InputName = 'controls';Les noms en entrée s’étendent automatiquement à {'controls(1)';'controls(2)'}.
Vous pouvez utiliser la notation abrégée u pour faire référence à la propriété InputName. Par exemple, sys.u est équivalent à sys.InputName.
Utilisez InputName pour :
Identifier des canaux sur l’affichage et les tracés du modèle.
Extraire des sous-systèmes de systèmes MIMO.
Spécifier des points de connexion au moment d’interconnecter les modèles.
Unités des canaux en entrée spécifiées sous l’une des formes suivantes :
Vecteur de caractères pour les modèles à entrée unique.
Cell array de vecteurs de caractères pour les modèles à entrées multiples.
'', pas d'unité spécifiée pour les canaux en entrée.
Utilisez InputUnit pour spécifier les unités des signaux en entrée. InputUnit n'a aucune incidence sur le comportement du système.
Groupes de canaux en entrée spécifiés en tant que structure. Utilisez InputGroup pour attribuer les canaux en entrée des systèmes MIMO à des groupes et faire référence à chaque groupe par son nom. Les noms des champs de InputGroup correspondent aux noms des groupes tandis que les valeurs des champs sont les canaux en entrée pour chaque groupe. Par exemple, saisissez ce qui suit pour créer des groupes d’entrée nommés controls et noise comprenant respectivement les canaux d’entrée 1, 2, 3 et 5.
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
Vous pouvez alors extraire le sous-système des entrées controls vers toutes les sorties en utilisant la commande suivante.
sys(:,'controls')Par défaut, InputGroup est une structure dépourvue de champs.
Noms des canaux en sortie spécifiés sous l’une des formes suivantes :
Vecteur de caractères pour les modèles à sortie unique.
Cell array de vecteurs de caractères pour les modèles à sorties multiples.
'', pas de nom spécifié pour les canaux en sortie.
Sinon, vous pouvez attribuer des noms de sortie pour les modèles à sorties multiples au moyen de l'expansion vectorielle automatique. Par exemple, si sys est un modèle à deux sorties, saisissez ce qui suit :
sys.OutputName = 'measurements';Les noms de sortie s’étendent automatiquement à {'measurements(1)';'measurements(2)'}.
Vous pouvez également utiliser la notation abrégée y pour faire référence à la propriété OutputName. Par exemple, sys.y est équivalent à sys.OutputName.
Utilisez OutputName pour :
Identifier des canaux sur l’affichage et les tracés du modèle.
Extraire des sous-systèmes de systèmes MIMO.
Spécifier des points de connexion au moment d’interconnecter les modèles.
Unités des canaux en sortie spécifiées sous l’une des formes suivantes :
Vecteur de caractères pour les modèles à sortie unique.
Cell array de vecteurs de caractères pour les modèles à sorties multiples.
'', pas d'unité spécifiée pour les canaux en sortie.
Utilisez OutputUnit pour spécifier les unités des signaux en sortie. OutputUnit n'a aucune incidence sur le comportement du système.
Groupes de canaux en sortie spécifiés en tant que structure. Utilisez OutputGroup pour attribuer les canaux en sortie des systèmes MIMO à des groupes et faire référence à chaque groupe par son nom. Les noms des champs de OutputGroup correspondent aux noms des groupes tandis que les valeurs des champs sont les canaux en sortie pour chaque groupe. Par exemple, créez des groupes de sortie nommés temperature et measurement et comprenant respectivement les canaux de sortie 1, 3 et 5.
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
Vous pouvez alors extraire le sous-système de toutes les entrées vers les sorties measurement en utilisant la commande suivante.
sys('measurement',:)Par défaut, OutputGroup est une structure dépourvue de champs.
Nom du système spécifié en tant que vecteur de caractères. Par exemple, 'system_1'.
Texte spécifié par l’utilisateur, que vous souhaitez associer au système, spécifié en tant que vecteur de caractères ou cell array de vecteurs de caractères. Par exemple, 'System is MIMO'.
Données spécifiées par l’utilisateur, que vous souhaitez associer au système, spécifié en tant que type de données MATLAB.
Grille d’échantillonnage pour les tableaux de modèles, spécifiés en tant que structure array.
Utilisez SamplingGrid pour effectuer le suivi des valeurs variables associées à chaque modèle dans un tableau de modèles, y compris les tableaux de modèles linéaires identifiés fixes dans le temps (IDLTI).
Définissez les noms des champs de la structure sur les noms des variables d'échantillonnage. Définissez les valeurs des champs sur les valeurs variables échantillonnées associées à chaque modèle du tableau. Toutes les variables d'échantillonnage doivent être des scalaires numériques et tous les tableaux de valeurs échantillonnées doivent correspondre aux dimensions du tableau de modèles.
Par exemple, vous pouvez créer un tableau 11 par 1 de modèles linéaires, sysarr, en prenant des snapshots d'un système linéaire variant dans le temps à des moments t = 0:10. Le code suivant stocke les pas d’échantillonnage avec les modèles linéaires.
sysarr.SamplingGrid = struct('time',0:10)De la même manière, vous pouvez créer un tableau de modèles 6 par 9, M, en échantillonnant indépendamment deux variables, zeta et w. Le code suivant fait correspondre les valeurs (zeta,w) à M.
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
Lorsque vous affichez M, chaque entrée du tableau comprend les valeurs zeta et w correspondantes.
M
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...Pour les tableaux de modèles générés par linéarisation d'un modèle Simulink® à valeurs de paramètres ou points de fonctionnement multiples, le software remplit automatiquement SamplingGrid avec les valeurs de variables qui correspondent à chaque entrée du tableau. Par exemple, les commandes Simulink Control Design™ linearize (Simulink Control Design) et slLinearizer (Simulink Control Design) remplissent automatiquement SamplingGrid.
Par défaut, SamplingGrid est une structure dépourvue de champs.
Fonctions d'objet
Les listes suivantes contiennent un sous-ensemble représentatif des fonctions que vous pouvez utiliser avec les modèles zpk. En règle générale, toute fonction applicable à Modèles de systèmes dynamiques est applicable à un objet zpk.
step | Réponse indicielle d’un système dynamique |
impulse | Impulse response plot of dynamic system; impulse response data |
lsim | Compute time response simulation data of dynamic system to arbitrary inputs |
bode | Réponse en fréquence de Bode d'un système dynamique |
nyquist | Nyquist response of dynamic system |
nichols | Réponse de Black-Nichols d’un système dynamique |
bandwidth | Frequency response bandwidth |
pidtune | PID tuning algorithm for linear plant model |
rlocus | Lieu des racines d’un système dynamique |
lqr | Design d'un régulateur linéaire quadratique (LQR, Linear Quadratic Regulator) |
lqg | Linear-Quadratic-Gaussian (LQG) design |
lqi | Contrôle linéaire quadratique intégral |
kalman | Design Kalman filter for state estimation |
Exemples
Pour les besoins de cet exemple, considérons le modèle SISO zéro-pôle-gain en temps continu suivant :
Spécifiez les zéros, les pôles et le gain, et créez le modèle SISO zéro-pôle-gain.
zeros = 0; poles = [1-1i 1+1i 2]; gain = -2; sys = zpk(zeros,poles,gain)
sys =
-2 s
--------------------
(s-2) (s^2 - 2s + 2)
Continuous-time zero/pole/gain model.
Model Properties
Pour cet exemple, considérons le modèle SISO zéro-pôle-gain en temps discret suivant, avec un pas d’échantillonnage de 0,1 s :
Spécifiez les zéros, les pôles et le gain, ainsi que le pas d’échantillonnage, et créez le modèle SISO zéro-pôle-gain en temps discret.
zeros = [1 2 3]; poles = [6 5 4]; gain = 7; ts = 0.1; sys = zpk(zeros,poles,gain,ts)
sys = 7 (z-1) (z-2) (z-3) ------------------- (z-6) (z-5) (z-4) Sample time: 0.1 seconds Discrete-time zero/pole/gain model. Model Properties
Dans cet exemple, vous créez un modèle MIMO zéro-pole-gain en concaténant des modèles SISO zéro-pole-gain. Considérons le modèle zéro-pôle-gain en temps continu à une entrée et deux sorties suivant :
Spécifiez le modèle MIMO zéro-pôle-gain en concaténant les entrées SISO.
zeros1 = 1; poles1 = -1; gain = 1; sys1 = zpk(zeros1,poles1,gain)
sys1 = (s-1) ----- (s+1) Continuous-time zero/pole/gain model. Model Properties
zeros2 = -2; poles2 = [-2+1i -2-1i]; sys2 = zpk(zeros2,poles2,gain)
sys2 =
(s+2)
--------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
sys = [sys1;sys2]
sys =
From input to output...
(s-1)
1: -----
(s+1)
(s+2)
2: --------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
Créez un modèle zéro-pôle-gain en temps discret, à entrées et sorties multiples :
avec un pas d’échantillonnage de ts = 0.2 secondes.
Spécifiez les zéros et pôles sous la forme de cell arrays et les gains sous la forme d’un tableau.
zeros = {[] 0;2 []};
poles = {-0.3 -0.3;-0.3 -0.3};
gain = [1 1;-1 3];
ts = 0.2;Créez un modèle MIMO zéro-pôle-gain en temps discret.
sys = zpk(zeros,poles,gain,ts)
sys =
From input 1 to output...
1
1: -------
(z+0.3)
- (z-2)
2: -------
(z+0.3)
From input 2 to output...
z
1: -------
(z+0.3)
3
2: -------
(z+0.3)
Sample time: 0.2 seconds
Discrete-time zero/pole/gain model.
Model Properties
Spécifiez les zéros, pôles et le gain, ainsi que le pas d’échantillonnage et créez le modèle zéro-pôle-gain en spécifiant les noms des noms d’état et d’entrée au moyen de paires nom-valeur.
zeros = 4; poles = [-1+2i -1-2i]; gain = 3; ts = 0.05; sys = zpk(zeros,poles,gain,ts,'InputName','Force')
sys =
From input "Force" to output:
3 (z-4)
--------------
(z^2 + 2z + 5)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Model Properties
Le nombre de noms d’entrée doit être cohérent avec le nombre de zéros.
Il peut être utile d’attribuer des noms aux entrées et aux sorties lorsque vous utilisez des tracés de réponse pour les systèmes MIMO.
step(sys)

Notez le nom de l'entrée Force dans le titre du tracé de réponse indicielle.
Pour cet exemple, créez un modèle zéro-pôle-gain en temps continu avec des expressions rationnelles. Il est parfois plus aisé et plus intuitif de recourir à une expression rationnelle plutôt que de spécifier des pôles et des zéros.
Considérons le système suivant :
Pour créer le modèle de fonction de transfert, commencez par spécifier s en tant qu’objet zpk.
s = zpk('s')s = s Continuous-time zero/pole/gain model. Model Properties
Créez le modèle zéro-pôle-gain en utilisant s dans l’expression rationnelle.
sys = s/(s^2 + 2*s + 10)
sys =
s
---------------
(s^2 + 2s + 10)
Continuous-time zero/pole/gain model.
Model Properties
Pour cet exemple, créez un modèle zéro-pôle-gain en temps discret au moyen d’une expression rationnelle. Il est parfois plus aisé et plus intuitif de recourir à une expression rationnelle plutôt que de spécifier des pôles et des zéros.
Considérons le système suivant :
Pour créer le modèle zéro-pôle-gain, commencez par spécifier z en tant qu’objet zpk et le pas d’échantillonnage ts.
ts = 0.1;
z = zpk('z',ts)z = z Sample time: 0.1 seconds Discrete-time zero/pole/gain model. Model Properties
Créez le modèle zéro-pôle-gain en utilisant z dans l’expression rationnelle.
sys = (z - 1) / (z^2 - 1.85*z + 0.9)
sys =
(z-1)
-------------------
(z^2 - 1.85z + 0.9)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
Model Properties
Pour cet exemple, créez un modèle zéro-pôle-gain avec les propriétés héritées d’un autre modèle du même type. Considérons les deux modèles zéro-pôle-gain suivants :
Pour cet exemple, créez sys1 en configurant les propriétés TimeUnit et InputDelay en minutes.
zero1 = 0; pole1 = [0;-8]; gain1 = 2; sys1 = zpk(zero1,pole1,gain1,'TimeUnit','minutes','InputUnit','minutes')
sys1 =
2 s
-------
s (s+8)
Continuous-time zero/pole/gain model.
Model Properties
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1×2 cell
{'minutes'} {'minutes'}
Créez le deuxième modèle zéro-pôle-gain avec les propriétés héritées de sys1.
zero = 1; pole = [-3,5]; gain2 = 0.8; sys2 = zpk(zero,pole,gain2,sys1)
sys2 = 0.8 (s-1) ----------- (s+3) (s-5) Continuous-time zero/pole/gain model. Model Properties
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1×2 cell
{'minutes'} {'minutes'}
Comme vous pouvez le constater, le modèle zéro-pôle-gain sys2 comporte les mêmes propriétés que sys1.
Considérons la matrice de gain statique suivante à deux entrées et deux sorties m :
Spécifiez la matrice de gain et créez le modèle zéro-pôle-gain à gain statique.
m = [2,4;...
3,5];
sys1 = zpk(m)sys1 = From input 1 to output... 1: 2 2: 3 From input 2 to output... 1: 4 2: 5 Static gain. Model Properties
Vous pouvez utiliser le modèle zéro-pôle-gain à gain statique sys1 obtenu précédemment et l’organiser en cascade avec un autre modèle du même type.
sys2 = zpk(0,[-1 7],1)
sys2 =
s
-----------
(s+1) (s-7)
Continuous-time zero/pole/gain model.
Model Properties
sys = series(sys1,sys2)
sys =
From input 1 to output...
2 s
1: -----------
(s+1) (s-7)
3 s
2: -----------
(s+1) (s-7)
From input 2 to output...
4 s
1: -----------
(s+1) (s-7)
5 s
2: -----------
(s+1) (s-7)
Continuous-time zero/pole/gain model.
Model Properties
Pour cet exemple, calculez le modèle zéro-pôle-gain du modèle de représentation d’état suivant :
Créez le modèle de représentation d’état au moyen des matrices de représentation d’état.
A = [-2 -1;1 -2]; B = [1 1;2 -1]; C = [1 0]; D = [0 1]; ltiSys = ss(A,B,C,D);
Convertissez le modèle de représentation d’état ltiSys en un modèle zéro-pôle-gain.
sys = zpk(ltiSys)
sys =
From input 1 to output:
s
--------------
(s^2 + 4s + 5)
From input 2 to output:
(s^2 + 5s + 8)
--------------
(s^2 + 4s + 5)
Continuous-time zero/pole/gain model.
Model Properties
Vous pouvez utiliser une boucle for pour spécifier un tableau de modèles zéro-pôle-gain.
Commencez par pré-attribuer le tableau des modèles zéro-pôle-gain avec des zéros.
sys = zpk(zeros(1,1,3));
Les deux premiers indices représentent le nombre de sorties et d'entrées pour les modèles, tandis que le troisième indice correspond au nombre de modèles figurant dans le tableau.
Créez le tableau de modèles zéro-pôle-gain en utilisant une expression rationnelle dans la boucle for.
s = zpk('s'); for k = 1:3 sys(:,:,k) = k/(s^2+s+k); end sys
sys(:,:,1,1) =
1
-------------
(s^2 + s + 1)
sys(:,:,2,1) =
2
-------------
(s^2 + s + 2)
sys(:,:,3,1) =
3
-------------
(s^2 + s + 3)
3x1 array of continuous-time zero/pole/gain models.
Model Properties
Pour cet exemple, extrayez la composante mesurée et la composante de bruit d’un modèle polynomial identifié vers deux modèles zéro-pôle-gain distincts.
Chargez le modèle polynomial de Box-Jenkins ltiSys dans identifiedModel.mat.
load('identifiedModel.mat','ltiSys');
ltiSys est un modèle identifié en temps discret du type : où représente la composante mesurée et , la composante de bruit.
Extrayez la composante mesurée et la composante de bruit en tant que modèles zéro-pôle-gain.
sysMeas = zpk(ltiSys,'measured') sysMeas =
From input "u1" to output "y1":
-0.14256 z^-1 (1-1.374z^-1)
z^(-2) * -----------------------------
(1-0.8789z^-1) (1-0.6958z^-1)
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties
sysNoise = zpk(ltiSys,'noise')sysNoise =
From input "v@y1" to output "y1":
0.045563 (1+0.7245z^-1)
--------------------------------------------
(1-0.9658z^-1) (1 - 0.0602z^-1 + 0.2018z^-2)
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties
La composante mesurée peut servir de modèle de système physique tandis que la composante de bruit peut être utilisée en tant que modèle de perturbations pour le design du système de contrôle.
Pour cet exemple, créez un modèle SISO zéro-pôle-gain avec un retard en entrée de 0,5 seconde et un retard en sortie de 2,5 secondes.
zeros = 5; poles = [7+1i 7-1i -3]; gains = 1; sys = zpk(zeros,poles,gains,'InputDelay',0.5,'OutputDelay',2.5)
sys =
(s-5)
exp(-3*s) * ----------------------
(s+3) (s^2 - 14s + 50)
Continuous-time zero/pole/gain model.
Model Properties
Vous pouvez également utiliser la commande get pour afficher toutes les propriétés d’un objet MATLAB.
get(sys)
Z: {[5]}
P: {[3×1 double]}
K: 1
DisplayFormat: 'roots'
Variable: 's'
IODelay: 0
InputDelay: 0.5000
OutputDelay: 2.5000
InputName: {''}
InputUnit: {''}
InputGroup: [1×1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ''
Ts: 0
TimeUnit: 'seconds'
SamplingGrid: [1×1 struct]
Pour plus d'informations sur la spécification d’un retard pour un modèle LTI, consultez Specifying Time Delays.
Pour cet exemple, concevez un contrôleur PID 2-DOF avec une bande passante cible de 0,75 rad/s pour un système représenté par le modèle zéro-pôle-gain suivant :
Créez un objet modèle zéro-pôle-gain sys au moyen de la commande zpk.
zeros = []; poles = [-0.25+0.2i;-0.25-0.2i]; gain = 1; sys = zpk(zeros,poles,gain)
sys =
1
---------------------
(s^2 + 0.5s + 0.1025)
Continuous-time zero/pole/gain model.
Model Properties
Au moyen de la bande passante cible, utilisez pidtune pour générer un contrôleur 2-DOF.
wc = 0.75;
C2 = pidtune(sys,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 0.512, Ki = 0.0975, Kd = 0.574, b = 0.38, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Model Properties
Lorsque le type 'PID2' est utilisé, pidtune génère un contrôleur 2-DOF représenté en tant qu’objet pid2. L’affichage confirme ce résultat. L’affichage indique également que pidtune règle tous les coefficients du contrôleur, y compris les poids des points de consigne b et c, pour équilibrer la performance et la robustesse.
Pour en savoir plus sur le réglage PID interactif dans le Live Editor, voir la tâche Tune PID Controller Live Editor. Cette tâche vous permet de concevoir un contrôleur PID de manière interactive et génère automatiquement un code MATLAB pour votre live script.
Pour effectuer un réglage PID interactif dans une application autonome, utilisez PID Tuner. Pour consulter un exemple de conception d’un contrôleur au moyen de l’application, voir Design d'un contrôleur PID pour le suivi rapide des consignes.
Depuis R2025a
Cet exemple indique comment obtenir un modèle zéro-pôle-gain tronqué d’un modèle de représentation d’état parcimonieux. Cet exemple utilise un modèle parcimonieux obtenu à partir de la linéarisation d’un modèle thermique de distribution de la chaleur dans une tige de vérin circulaire.
Chargez les données du modèle.
load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.
Analysez la réponse en fréquence du modèle.
sigmaplot(sys,w)
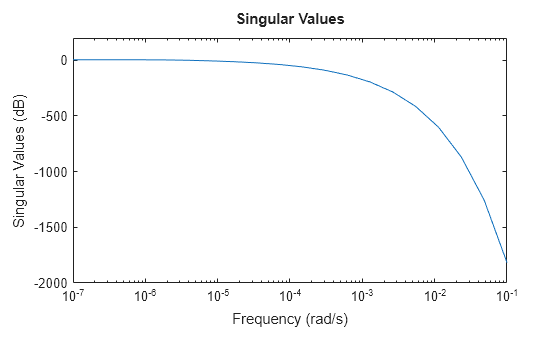
Pour obtenir une approximation tronquée, utilisez zpk et spécifiez la bande de fréquence d’attention. Pour ce modèle, vous pouvez utiliser une plage de fréquence de 0 rad/s à 0,01 rad/s pour obtenir l’approximation d’ordre faible.
zsys = zpk(sys,Focus=[0 1e-2],Display="off");Comparez la réponse en fréquence.
sigmaplot(sys,zsys,w)
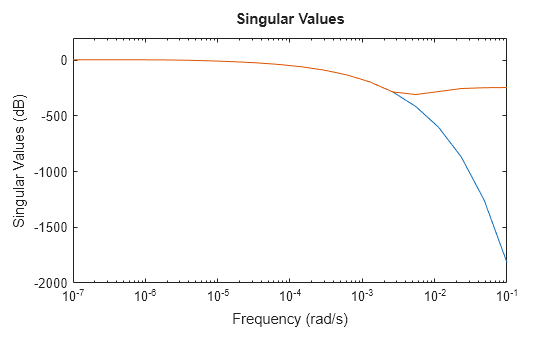
Ce modèle thermique présente une atténuation très abrupte sous 0,001 rad/s. Par défaut, le modèle réduit obtenu au moyen de zpk ne fournit pas de bonne correspondance à cette atténuation. Pour atténuer cela, vous pouvez utiliser l’argument RollOff de zpk et spécifier une valeur d’atténuation minimale au-delà de la bande de fréquence d’attention. Spécifiez une valeur de pente d’atténuation de -45, qui correspond à une vitesse d’au moins –900 dB/décade.
zsys2 = zpk(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,zsys2,w)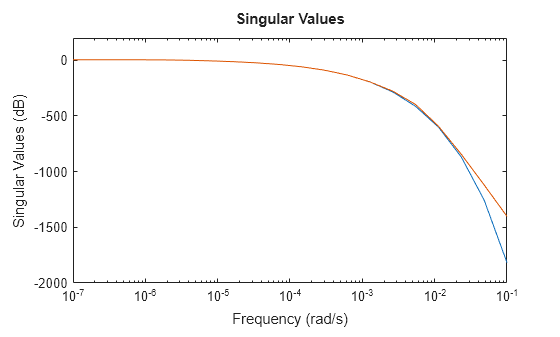
Le modèle réduit fournit maintenant une bien meilleure approximation de la valeur d’atténuation. Cependant, dans cet exemple, réajuster la pente d’atténuation au moyen de zpk nécessite de recalculer les zéros et les pôles. Cela pourrait devenir coûteux en calcul dans le cas de modèles à grande échelle. Comme alternative, vous pouvez utiliser la méthode de troncature zéro-pôle de reducespec et ajuster l’atténuation sans coût de calcul supplémentaire, après que le logiciel a calculé les pôles et les zéros. Pour un exemple, voir Zero-Pole Truncation of Thermal Model.
Algorithmes
zpk utilise la fonction MATLAB roots pour convertir des fonctions de transfert et les fonctions zero et pole pour convertir des modèles de représentation d’état.
Pour convertir des modèles parcimonieux, zpk utilise l’algorithme de Krylov-Schur [1] pour les itérations de puissance inverse pour calculer les pôles et les zéros dans la bande de fréquence.
Références
[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.
Historique des versions
Introduit avant R2006aVous pouvez maintenant utiliser zpk pour convertir des modèles de représentation d’état parcimonieux et obtenir une approximation zéro-pôle-gain tronquée. zpk calcule un sous-ensemble des zéros et des pôles des modèles parcimonieux, généralement dans une bande basse fréquence spécifique [0 fmax]. Cela permet d’obtenir de meilleures approximations basse fréquence que la réduction d’ordre de modèle par troncature modale au prix de calculs supplémentaires. zpk fournit également un contrôle direct sur la pente d’atténuation après la fréquence fmax. Utilisez la nouvelle syntaxe zsys = zpk(sparseSys,Name=Value) pour obtenir une approximation basée sur les options spécifiées, telles que la plage de fréquences d’attention. Pour un exemple, voir Calculer l’approximation ZPK tronquée d’un modèle parcimonieux.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)